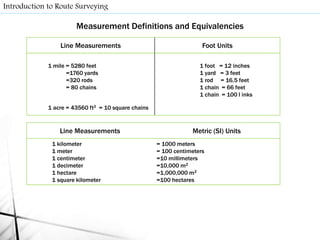
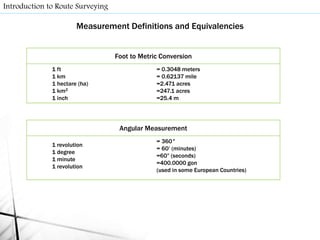
- Surveying involves making field measurements on or near the Earth's surface to determine relative positions of points or establish points. It includes preliminary surveys to collect data, layout surveys to define proposed construction locations, and construction surveys to provide line and grade during construction. - Control surveys establish horizontal and vertical reference points and lines that preliminary and construction surveys are referenced to. Horizontal control may be tied to grid monuments, property lines, or baselines while vertical control uses benchmark elevations from leveling surveys. 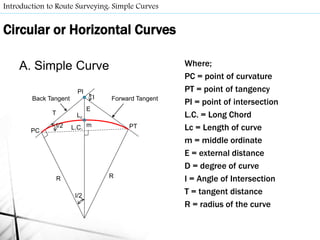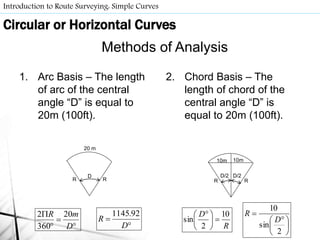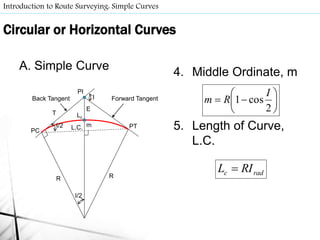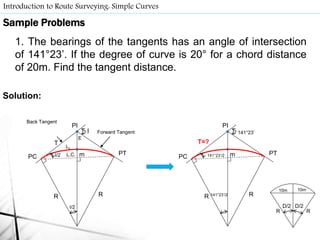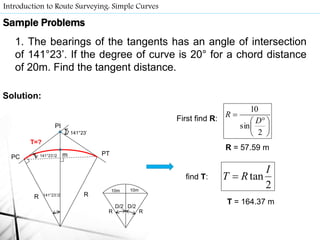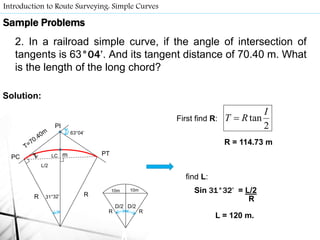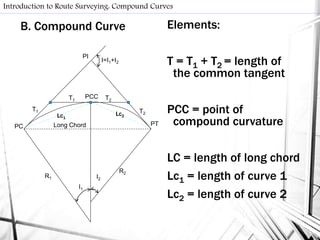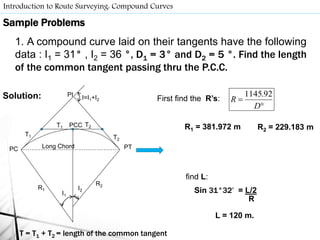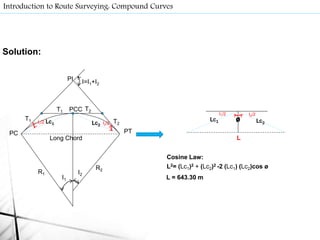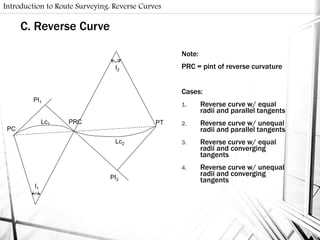- Route surveys initially layout highways as a series of tangents joined by circular curves. Compound curves consist of two or more joining circular arcs between main tangents turning in the same direction. Reverse curves connect lines through

1. GE 102
Construction and
Industrial Surveys

2. Surveying?
- is the art and science of making field
measurements on or near the surface of the Earth.
(Kavanagh)
- is the science and art of determining relative
positions of points above, on, or beneath the
surface of the earth, or establishing such points.
(Brinker and Wolf)
Introduction to Construction and Industrial Surveys

3. Purpose of Surveying?
- Made to collect data, which can be drawn to
scale on a plan or map. (Preliminary Surveys)
- Made to layout dimensions shown on a design
plan in order to precisely define the field
location for the proposed construction facility.
The layouts of proposed property lines and corners as
required in land division are called “Layout Surveys”.
Introduction to Construction and Industrial Surveys

4. The layouts of proposed construction features are
called “Construction Surveys”.
Preliminary & Construction Surveys
Both surveys must be reference to a common base
for X, Y and Z dimensions.
The establishment of a base horizontal and vertical
measurements is known as “Control Surveys”.
Introduction to Construction and Industrial Surveys

5. Introduction to Construction and Industrial Surveys
Control Surveys
- Establish reference points and reference lines for
the preliminary and construction surveys.
- Vertical reference points called benchmarks, are
established using Leveling Surveys.
- Horizontal control surveys can be tied into
• State or Provincial coordinate grid monuments
• Property lines
• Roadway centerlines
• Arbitrary places baselines or grids.

6. Introduction to Construction and Industrial Surveys
Construction Surveys
- Provide line and grade for a wide variety of
construction projects (highways, streets,
pipelines, bridges, buildings, & site grading).
Line – horizontal location
Grade – vertical location/elevation

7. Measurement Definitions and Equivalencies
Line Measurements Foot Units
1 mile = 5280 feet
=1760 yards
=320 rods
= 80 chains
1 foot = 12 inches
1 yard = 3 feet
1 rod = 16.5 feet
1 chain = 66 feet
1 chain = 100 l inks
1 acre = 43560 ft2 = 10 square chains
Line Measurements Metric (SI) Units
1 kilometer
1 meter
1 centimeter
1 decimeter
1 hectare
1 square kilometer
= 1000 meters
= 100 centimeters
=10 millimeters
=10,000 m2
=1,000,000 m2
=100 hectares
Introduction to Route Surveying

8. Measurement Definitions and Equivalencies
Foot to Metric Conversion
1 ft
1 km
1 hectare (ha)
1 km2
1 inch
= 0.3048 meters
= 0.62137 mile
=2.471 acres
=247.1 acres
=25.4 m
Angular Measurement
1 revolution
1 degree
1 minute
1 revolution
= 360°
= 60’ (minutes)
=60” (seconds)
=400.0000 gon
(used in some European Countries)
Introduction to Route Surveying

9. Introduction to Route Surveying
Errors – Random and Systematic
Errors – difference between a measured or
observed value and the true value.
 Systematic Errors
-those errors for which the magnitude and
the algebraic sign can be determined.
 Random Errors (accidental errors)
- associated with the skill and vigilance of
the surveyor.
- are introduced into each measurement
mainly because no human can perform
perfectly.

10. Introduction to Route Surveying
Mistakes
- are blunders made by survey personnel.
Examples of Mistakes
 transposing figures
 miscounting the number of full tape lengths in
a long measurement
 measuring to or from a wrong point

11. Introduction to Route Surveying
Route Surveys
- Initially laid out as a series of straight lines
(tangents). Once the location alignment has
been confirmed, the tangents are joined by
circular curves that allow for smooth vehicle
operation at the speeds for which the highway is
designed.

12. Introduction to Route Surveying: Simple Curves
Circular or Horizontal Curves
A. Simple Curve Where;
PC = point of curvature
PT = point of tangency
PI = point of intersection
L.C. = Long Chord
Lc = Length of curve
m = middle ordinate
E = external distance
D = degree of curve
I = Angle of Intersection
T = tangent distance
R = radius of the curve
Forward TangentIBack Tangent
I/2
RR
Lc
L.C.I/2
PC
PI
PTm
E
T

13. Methods of Analysis
1. Arc Basis – The length
of arc of the central
angle “D” is equal to
20m (100ft).
2. Chord Basis – The
length of chord of the
central angle “D” is
equal to 20m (100ft).
D
20 m
RR
D/2
RR
D/2
10m 10m




D
mR 20
360
2


D
R
92.1145
R
D 10
2
sin 




 





 

2
sin
10
D
R
Introduction to Route Surveying: Simple Curves
Circular or Horizontal Curves

14. Formula’s
1. Tangent Distance, T
2. Long Chord, L
3. External Distance, E
4. Middle Ordinate, m
5. Length of Curve,
L.C.
2
tan
I
RT 
2
sin2
I
RL 






 1
2
sec
I
RE







2
cos1
I
Rm
radc RIL 
Introduction to Route Surveying: Simple Curves
Circular or Horizontal Curves

15. Introduction to Route Surveying: Simple Curves
Circular or Horizontal Curves
A. Simple Curve
Forward TangentIBack Tangent
I/2
RR
Lc
L.C.I/2
PC
PI
PTm
E
T
1. Tangent Distance, T
2. Long Chord, L
3. External Distance, E
2
tan
I
RT 
2
sin2
I
RL 






 1
2
sec
I
RE

16. Introduction to Route Surveying: Simple Curves
Circular or Horizontal Curves
A. Simple Curve
Forward TangentIBack Tangent
I/2
RR
Lc
L.C.I/2
PC
PI
PTm
E
T
4. Middle Ordinate, m
5. Length of Curve,
L.C.







2
cos1
I
Rm
radc RIL 

17. Introduction to Route Surveying: Simple Curves
Forward TangentI
Back Tangent
I/2
RR
Lc
L.C.I/2PC
PI
PTm
E
T
141°23’
RR
141°23’/2PC
PI
PTm
T=?
141°23’/2
D/2
RR
D/2
10m 10m
Sample Problems
1. The bearings of the tangents has an angle of intersection
of 141°23’. If the degree of curve is 20° for a chord distance
of 20m. Find the tangent distance.
Solution:

18. Introduction to Route Surveying: Simple Curves
141°23’
RR
141°23’/2PC
PI
PTm
T=?
141°23’/2
D/2
RR
D/2
10m 10m
First find R:





 

2
sin
10
D
R
R = 57.59 m
2
tan
I
RT find T:
T = 164.37 m
Sample Problems
1. The bearings of the tangents has an angle of intersection
of 141°23’. If the degree of curve is 20° for a chord distance
of 20m. Find the tangent distance.
Solution:

19. Introduction to Route Surveying: Simple Curves
63°04’
RR
PC
PI
PTm
D/2
RR
D/2
10m 10m
First find R:
find L:
Sample Problems
2. In a railroad simple curve, if the angle of intersection of
tangents is 63°04’. And its tangent distance of 70.40 m. What
is the length of the long chord?
Solution:
LC
2
tan
I
RT 
R = 114.73 m
L/2
Sin 31°32’ = L/2
R
L = 120 m.

20. B. Compound Curve
Introduction to Route Surveying: Compound Curves
Consist of two (usually) or more circular arcs between two
main tangents turning in the same direction and joining at
common tangent points.

21. B. Compound Curve Elements:
T = T1 + T2 = length of
the common tangent
PCC = point of
compound curvature
LC = length of long chord
Lc1 = length of curve 1
Lc2 = length of curve 2
I1
I2
R1
R2
T1 T2
T1
Long Chord
T2
PC
PCC
PT
PI
I=I1+I2
Introduction to Route Surveying: Compound Curves
Lc1
Lc2

22. First find the R’s:
find L:
Sample Problems
1. A compound curve laid on their tangents have the following
data : I1 = 31° , I2 = 36 °, D1 = 3° and D2 = 5 °. Find the length
of the common tangent passing thru the P.C.C.
Solution:
R1 = 381.972 m
Sin 31°32’ = L/2
R
L = 120 m.
Introduction to Route Surveying: Compound Curves
I1
I2R1
R2
T1 T2
T1
Long Chord
T2
PC
PCC
PT
PI I=I1+I2
T = T1 + T2 = length of the common tangent


D
R
92.1145
R2 = 229.183 m

23. 2. Two simple curves having angles of intersection of the
tangents equal to 36° and 68°45’ respectively are joined to
form a compound curve where the P.T of the first curve
becomes the PCC of the compound curve. If the length of
curve of the first curve is 427.14 m. and the length of curve
for the second curve is 235.21 m., find the length of curve
from the P.C, to the new compound curve.
Sample Problems
Introduction to Route Surveying: Compound Curves

24. Solution:
Introduction to Route Surveying: Compound Curves
I1
I2R1
R2
T1 T2
T1
Long Chord
T2
PC
PCC
PT
PI I=I1+I2
Lc1 Lc2
I1/2 Lc1 Lc2I2/2
L
I1/2 I2/2
Cosine Law:
L2= (Lc1)2 + (Lc2)2 -2 (Lc1) (Lc2)cos ø
ø
L = 643.30 m

25. Note:
PRC = pint of reverse curvature
Cases:
1. Reverse curve w/ equal
radii and parallel tangents
2. Reverse curve w/ unequal
radii and parallel tangents
3. Reverse curve w/ equal
radii and converging
tangents
4. Reverse curve w/ unequal
radii and converging
tangents
I1
I2
Lc1
Lc2
PRC
PC
PT
PI1
PI2
Introduction to Route Surveying: Reverse Curves
C. Reverse Curve

26. Sample Problems
1. Given the lines and direction as follows: AB = 57.6 m due east,
BC = 91.5 m., N 68° E, CD = 102.6 m., azimuth of 312 °. A
reverse curve is to connect these three lines thus forming the
center line of a new road. Compute the length of the common
radius of the reverse curves.
Solution:
Introduction to Route Surveying: Reverse Curves
T1 = R tan 11 °
T2 = R tan 32 °
T1 + T2 = 91.5 °
R tan 11 °+ R tan 32 ° = 91.5 °
R = 111.69 m

27. That’s all for today.