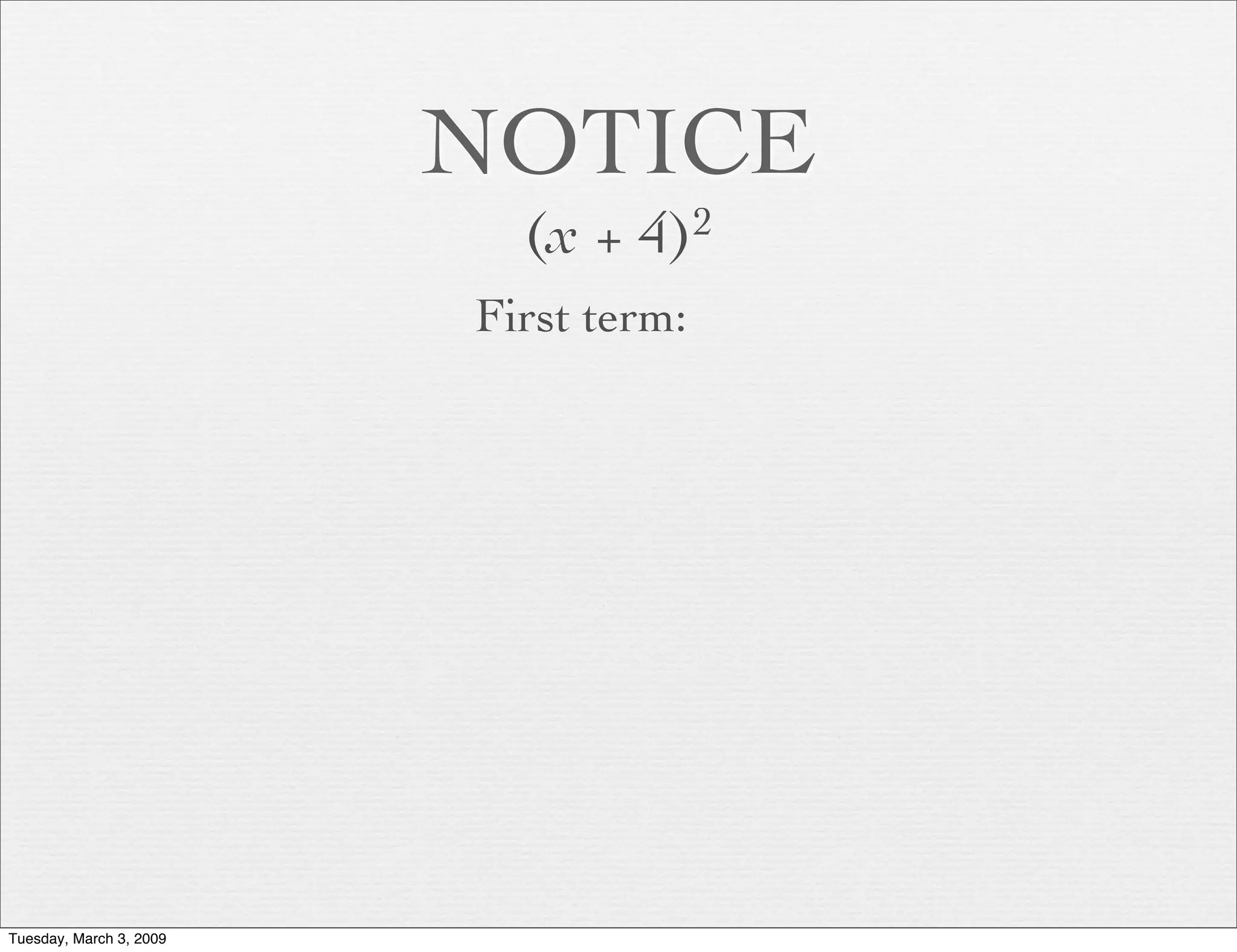
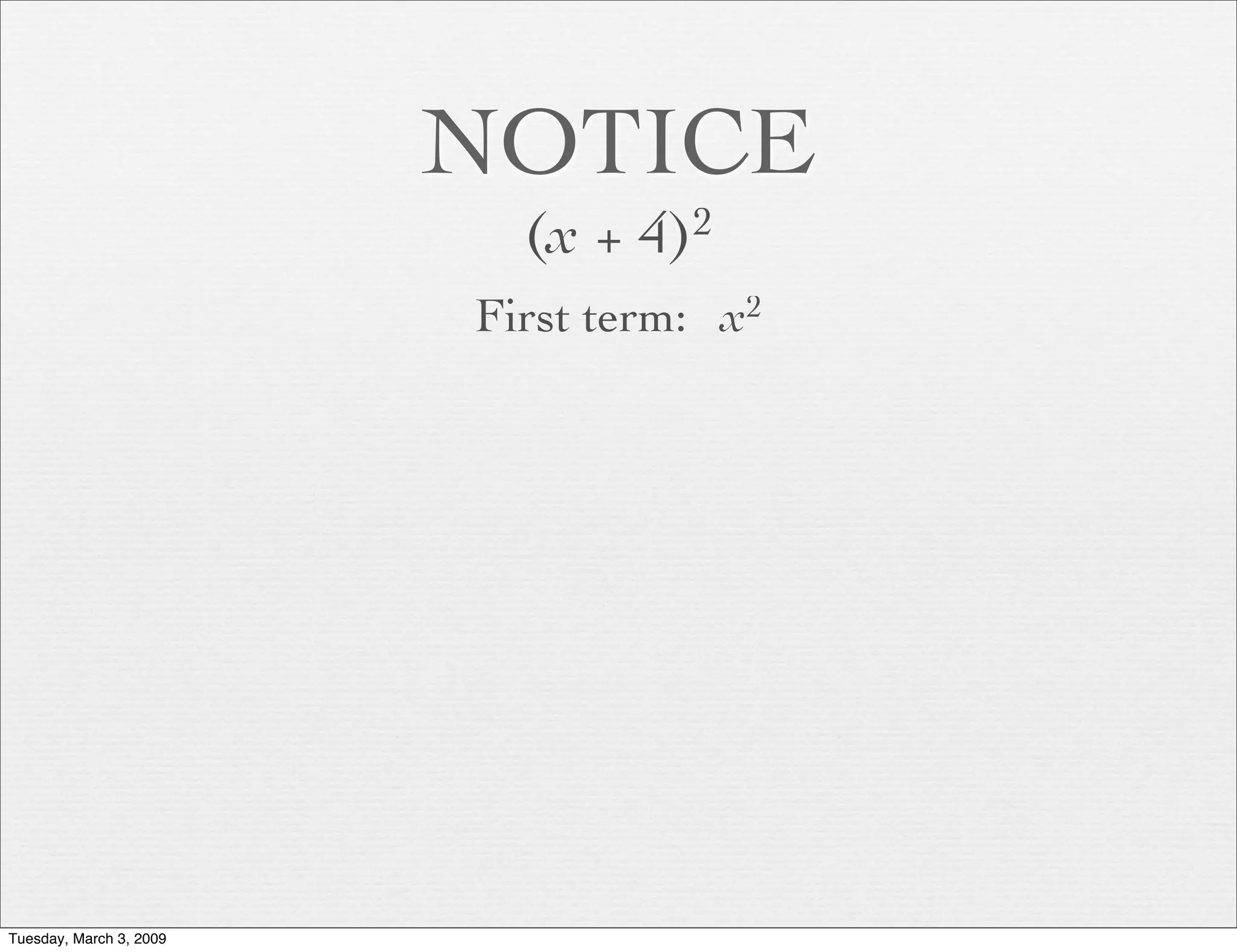
The document discusses various methods for factoring polynomials, including: 1. Greatest common factor (GCF) 2. Binomial square factoring 3. Difference of squares factoring It provides examples demonstrating how to use these methods to factor polynomials by finding common factors between terms. Specific techniques for binomial square factoring are explained, such as recognizing if a trinomial is a perfect square.

1. Section 11-3
Factoring Special Cases
Tuesday, March 3, 2009

2. Factoring:
Rewriting a polynomial as a product of factors
Tuesday, March 3, 2009

3. Factoring:
Rewriting a polynomial as a product of factors
1. Greatest Common Factor
Tuesday, March 3, 2009

4. Factoring:
Rewriting a polynomial as a product of factors
1. Greatest Common Factor
2. Binomial Square Factoring
Tuesday, March 3, 2009

5. Factoring:
Rewriting a polynomial as a product of factors
1. Greatest Common Factor
2. Binomial Square Factoring
3. Difference of Squares Factoring
Tuesday, March 3, 2009

6. Factoring:
Rewriting a polynomial as a product of factors
1. Greatest Common Factor
2. Binomial Square Factoring
3. Difference of Squares Factoring
4. Other Methods of Factoring
Tuesday, March 3, 2009

7. Factoring:
Rewriting a polynomial as a product of factors
1. Greatest Common Factor
2. Binomial Square Factoring
3. Difference of Squares Factoring
4. Other Methods of Factoring
There’s trial-and-error, too, but that just takes too long.
Tuesday, March 3, 2009

8. Example 1: Factor.
a. 12x2 - 4x b. 15x3y + 5x2y2 - 35xy2
Tuesday, March 3, 2009

9. Example 1: Factor.
a. 12x2 - 4x b. 15x3y + 5x2y2 - 35xy2
4
Tuesday, March 3, 2009

10. Example 1: Factor.
a. 12x2 - 4x b. 15x3y + 5x2y2 - 35xy2
4x
Tuesday, March 3, 2009

11. Example 1: Factor.
a. 12x2 - 4x b. 15x3y + 5x2y2 - 35xy2
4x(
Tuesday, March 3, 2009

12. Example 1: Factor.
a. 12x2 - 4x b. 15x3y + 5x2y2 - 35xy2
4x(3
Tuesday, March 3, 2009

13. Example 1: Factor.
a. 12x2 - 4x b. 15x3y + 5x2y2 - 35xy2
4x(3x
Tuesday, March 3, 2009

14. Example 1: Factor.
a. 12x2 - 4x b. 15x3y + 5x2y2 - 35xy2
4x(3x -
Tuesday, March 3, 2009

15. Example 1: Factor.
a. 12x2 - 4x b. 15x3y + 5x2y2 - 35xy2
4x(3x - 1
Tuesday, March 3, 2009

16. Example 1: Factor.
a. 12x2 - 4x b. 15x3y + 5x2y2 - 35xy2
4x(3x - 1)
Tuesday, March 3, 2009

17. Example 1: Factor.
a. 12x2 - 4x b. 15x3y + 5x2y2 - 35xy2
4x(3x - 1) 5
Tuesday, March 3, 2009

18. Example 1: Factor.
a. 12x2 - 4x b. 15x3y + 5x2y2 - 35xy2
4x(3x - 1) 5x
Tuesday, March 3, 2009

19. Example 1: Factor.
a. 12x2 - 4x b. 15x3y + 5x2y2 - 35xy2
4x(3x - 1) 5xy
Tuesday, March 3, 2009

20. Example 1: Factor.
a. 12x2 - 4x b. 15x3y + 5x2y2 - 35xy2
4x(3x - 1) 5xy(
Tuesday, March 3, 2009

21. Example 1: Factor.
a. 12x2 - 4x b. 15x3y + 5x2y2 - 35xy2
4x(3x - 1) 5xy(3x2 + xy - 7y)
Tuesday, March 3, 2009

22. Example 1: Factor.
a. 12x2 - 4x b. 15x3y + 5x2y2 - 35xy2
4x(3x - 1) 5xy(3x2 + xy - 7y)
All we did here was go through the numbers first, then the
variables in alphabetical order, finding factors that the terms
have in common.
Tuesday, March 3, 2009

23. Example 1: Factor.
a. 12x2 - 4x b. 15x3y + 5x2y2 - 35xy2
4x(3x - 1) 5xy(3x2 + xy - 7y)
All we did here was go through the numbers first, then the
variables in alphabetical order, finding factors that the terms
have in common.
To check your answer, re-distribute the GCF and see if you
get what you started with.
Tuesday, March 3, 2009

24. Binomial Square Factoring
Tuesday, March 3, 2009

25. Binomial Square Factoring
For all a and b:
Tuesday, March 3, 2009

26. Binomial Square Factoring
For all a and b:
a2 + 2ab + b2
Tuesday, March 3, 2009

27. Binomial Square Factoring
For all a and b:
a2 + 2ab + b2 = (a + b)2
Tuesday, March 3, 2009

28. Binomial Square Factoring
For all a and b:
a2 + 2ab + b2 = (a + b)2
a2 - 2ab + b2
Tuesday, March 3, 2009

29. Binomial Square Factoring
For all a and b:
a2 + 2ab + b2 = (a + b)2
a2 - 2ab + b2 = (a - b)2
Tuesday, March 3, 2009

30. Tuesday, March 3, 2009

31. (x + 4) 2
Tuesday, March 3, 2009

32. (x + 4) 2
(x + 4)(x + 4)
Tuesday, March 3, 2009

33. (x + 4) 2
(x + 4)(x + 4)
2 + 4x + 4x + 16
x
Tuesday, March 3, 2009

34. (x + 4) 2
(x + 4)(x + 4)
2 + 4x + 4x + 16
x
2 + 8x + 16
x
Tuesday, March 3, 2009

35. NOTICE
(x + 4) 2
First term:
Tuesday, March 3, 2009

36. NOTICE
(x + 4) 2
First term: x2
Tuesday, March 3, 2009

37. NOTICE
(x + 4) 2
First term: x2
What do you notice about it compared to what we
began with?
Tuesday, March 3, 2009

38. NOTICE
(x + 4) 2
First term: x2
What do you notice about it compared to what we
began with?
Middle term:
Tuesday, March 3, 2009

39. NOTICE
(x + 4) 2
First term: x2
What do you notice about it compared to what we
began with?
Middle term: 8x
Tuesday, March 3, 2009

40. NOTICE
(x + 4) 2
First term: x2
What do you notice about it compared to what we
began with?
Middle term: 8x
How does this compare with what we started out with?
Tuesday, March 3, 2009

41. NOTICE
(x + 4) 2
First term: x2
What do you notice about it compared to what we
began with?
Middle term: 8x
How does this compare with what we started out with?
Last term:
Tuesday, March 3, 2009

42. NOTICE
(x + 4) 2
First term: x2
What do you notice about it compared to what we
began with?
Middle term: 8x
How does this compare with what we started out with?
Last term: 16
Tuesday, March 3, 2009

43. NOTICE
(x + 4) 2
First term: x2
What do you notice about it compared to what we
began with?
Middle term: 8x
How does this compare with what we started out with?
Last term: 16
What’s happening?
Tuesday, March 3, 2009

44. A pattern emerges...
A perfect square trinomial will have the following things
occur:
Tuesday, March 3, 2009

45. A pattern emerges...
A perfect square trinomial will have the following things
occur:
1. The first term will be a perfect square.
Tuesday, March 3, 2009

46. A pattern emerges...
A perfect square trinomial will have the following things
occur:
1. The first term will be a perfect square.
2.The last term will be a perfect square.
Tuesday, March 3, 2009

47. A pattern emerges...
A perfect square trinomial will have the following things
occur:
1. The first term will be a perfect square.
2.The last term will be a perfect square.
3.The middle term will be 2 times the product of the square
roots of the first and last terms.
Tuesday, March 3, 2009

48. Example 2: Factor.
a. 9x2 + 12x + 4
Tuesday, March 3, 2009

49. Example 2: Factor.
a. 9x2 + 12x + 4
Check to see if the first and last terms are perfect squares.
Tuesday, March 3, 2009

50. Example 2: Factor.
a. 9x2 + 12x + 4
Check to see if the first and last terms are perfect squares.
Tuesday, March 3, 2009

51. Example 2: Factor.
a. 9x2 + 12x + 4
3x · 3x
Check to see if the first and last terms are perfect squares.
Tuesday, March 3, 2009

52. Example 2: Factor.
a. 9x2 + 12x + 4
3x · 3x
Check to see if the first and last terms are perfect squares.
3x
Tuesday, March 3, 2009

53. Example 2: Factor.
a. 9x2 + 12x + 4
3x · 3x
Check to see if the first and last terms are perfect squares.
3x
Tuesday, March 3, 2009

54. Example 2: Factor.
a. 9x2 + 12x + 4
3x · 3x 2·2
Check to see if the first and last terms are perfect squares.
3x
Tuesday, March 3, 2009

55. Example 2: Factor.
a. 9x2 + 12x + 4
3x · 3x 2·2
Check to see if the first and last terms are perfect squares.
3x 2
Tuesday, March 3, 2009

56. Example 2: Factor.
a. 9x2 + 12x + 4
3x · 3x 2·2
Check to see if the first and last terms are perfect squares.
3x 2
Check to see if the middle term is 2 times the product of the
square roots of the first and last terms.
Tuesday, March 3, 2009

57. Example 2: Factor.
a. 9x2 + 12x + 4
3x · 3x 2·2
Check to see if the first and last terms are perfect squares.
3x 2
Check to see if the middle term is 2 times the product of the
square roots of the first and last terms.
2(3x · 2)
Tuesday, March 3, 2009

58. Example 2: Factor.
a. 9x2 + 12x + 4
3x · 3x 2·2
Check to see if the first and last terms are perfect squares.
3x 2
Check to see if the middle term is 2 times the product of the
square roots of the first and last terms.
2(3x · 2) = 2(6x)
Tuesday, March 3, 2009

59. Example 2: Factor.
a. 9x2 + 12x + 4
3x · 3x 2·2
Check to see if the first and last terms are perfect squares.
3x 2
Check to see if the middle term is 2 times the product of the
square roots of the first and last terms.
2(3x · 2) = 2(6x) = 12x
Tuesday, March 3, 2009

60. Example 2: Factor.
a. 9x2 + 12x + 4
3x · 3x 2·2
Check to see if the first and last terms are perfect squares.
3x 2
Check to see if the middle term is 2 times the product of the
square roots of the first and last terms.
2(3x · 2) = 2(6x) = 12x
Final Answer:
Tuesday, March 3, 2009

61. Example 2: Factor.
a. 9x2 + 12x + 4
3x · 3x 2·2
Check to see if the first and last terms are perfect squares.
3x 2
Check to see if the middle term is 2 times the product of the
square roots of the first and last terms.
2(3x · 2) = 2(6x) = 12x
Final Answer:
(3x
Tuesday, March 3, 2009

62. Example 2: Factor.
a. 9x2 + 12x + 4
3x · 3x 2·2
Check to see if the first and last terms are perfect squares.
3x 2
Check to see if the middle term is 2 times the product of the
square roots of the first and last terms.
2(3x · 2) = 2(6x) = 12x
Final Answer:
(3x 2)
Tuesday, March 3, 2009

63. Example 2: Factor.
a. 9x2 + 12x + 4
3x · 3x 2·2
Check to see if the first and last terms are perfect squares.
3x 2
Check to see if the middle term is 2 times the product of the
square roots of the first and last terms.
2(3x · 2) = 2(6x) = 12x
Final Answer:
(3x + 2)
Tuesday, March 3, 2009

64. Example 2: Factor.
a. 9x2 + 12x + 4
3x · 3x 2·2
Check to see if the first and last terms are perfect squares.
3x 2
Check to see if the middle term is 2 times the product of the
square roots of the first and last terms.
2(3x · 2) = 2(6x) = 12x
Final Answer:
(3x + 2)2
Tuesday, March 3, 2009

65. Example 2: Factor.
b. x2 - 6x + 9 c. y2 - 20y + 100
d. x2 + 7x + 14
Tuesday, March 3, 2009

66. Example 2: Factor.
b. x2 - 6x + 9 c. y2 - 20y + 100
(x
d. x2 + 7x + 14
Tuesday, March 3, 2009

67. Example 2: Factor.
b. x2 - 6x + 9 c. y2 - 20y + 100
(x 3)
d. x2 + 7x + 14
Tuesday, March 3, 2009

68. Example 2: Factor.
b. x2 - 6x + 9 c. y2 - 20y + 100
(x - 3)
d. x2 + 7x + 14
Tuesday, March 3, 2009

69. Example 2: Factor.
b. x2 - 6x + 9 c. y2 - 20y + 100
(x - 3) 2
d. x2 + 7x + 14
Tuesday, March 3, 2009

70. Example 2: Factor.
b. x2 - 6x + 9 c. y2 - 20y + 100
(x - 3) 2 (y
d. x2 + 7x + 14
Tuesday, March 3, 2009

71. Example 2: Factor.
b. x2 - 6x + 9 c. y2 - 20y + 100
(x - 3) 2 (y -
d. x2 + 7x + 14
Tuesday, March 3, 2009

72. Example 2: Factor.
b. x2 - 6x + 9 c. y2 - 20y + 100
(x - 3) 2 (y - 10)
d. x2 + 7x + 14
Tuesday, March 3, 2009

73. Example 2: Factor.
b. x2 - 6x + 9 c. y2 - 20y + 100
(x - 3) 2 (y - 10)2
d. x2 + 7x + 14
Tuesday, March 3, 2009

74. Example 2: Factor.
b. x2 - 6x + 9 c. y2 - 20y + 100
(x - 3) 2 (y - 10)2
d. x2 + 7x + 14
(x
Tuesday, March 3, 2009

75. Example 2: Factor.
b. x2 - 6x + 9 c. y2 - 20y + 100
(x - 3) 2 (y - 10)2
d. x2 + 7x + 14
(x
14 is not a perfect square!
Cannot factor with this method.
Tuesday, March 3, 2009

76. Difference of Squares
Factoring
Tuesday, March 3, 2009

77. Difference of Squares
Factoring
For all a and b,
Tuesday, March 3, 2009

78. Difference of Squares
Factoring
For all a and b,
a2 - b2 =
Tuesday, March 3, 2009

79. Difference of Squares
Factoring
For all a and b,
a2 - b2 =
(a + b)(a - b)
Tuesday, March 3, 2009

80. Difference of two squares
This only works for the following conditions:
Tuesday, March 3, 2009

81. Difference of two squares
This only works for the following conditions:
1. You must have a binomial.
Tuesday, March 3, 2009

82. Difference of two squares
This only works for the following conditions:
1. You must have a binomial.
2.Both terms must be perfect squares.
Tuesday, March 3, 2009

83. Difference of two squares
This only works for the following conditions:
1. You must have a binomial.
2.Both terms must be perfect squares.
3.There must be subtraction!
Tuesday, March 3, 2009

84. (t - 5)(t + 5)
Tuesday, March 3, 2009

85. (t - 5)(t + 5)
= t2
Tuesday, March 3, 2009

86. (t - 5)(t + 5)
= t2+ 5t
Tuesday, March 3, 2009

87. (t - 5)(t + 5)
= t2+ 5t - 5t
Tuesday, March 3, 2009

88. (t - 5)(t + 5)
= t2+ 5t - 5t - 25
Tuesday, March 3, 2009

89. (t - 5)(t + 5)
= t2+ 5t - 5t - 25
= t2 - 25
Tuesday, March 3, 2009

90. Example 3: Factor.
a. 64x2 - 81
Tuesday, March 3, 2009

91. Example 3: Factor.
a. 64x2 - 81
Check to see if the first and last terms are perfect squares.
Tuesday, March 3, 2009

92. Example 3: Factor.
a. 64x2 - 81
Check to see if the first and last terms are perfect squares.
Tuesday, March 3, 2009

93. Example 3: Factor.
a. 64x2 - 81
8x · 8x
Check to see if the first and last terms are perfect squares.
Tuesday, March 3, 2009

94. Example 3: Factor.
a. 64x2 - 81
8x · 8x
Check to see if the first and last terms are perfect squares.
Tuesday, March 3, 2009

95. Example 3: Factor.
a. 64x2 - 81
8x · 8x 9 · 9
Check to see if the first and last terms are perfect squares.
Tuesday, March 3, 2009

96. Example 3: Factor.
a. 64x2 - 81
8x · 8x 9 · 9
Check to see if the first and last terms are perfect squares.
Is it a subtraction problem?
Tuesday, March 3, 2009

97. Example 3: Factor.
a. 64x2 - 81
8x · 8x 9 · 9
Check to see if the first and last terms are perfect squares.
Is it a subtraction problem?
Answer:
Tuesday, March 3, 2009

98. Example 3: Factor.
a. 64x2 - 81
8x · 8x 9 · 9
Check to see if the first and last terms are perfect squares.
Is it a subtraction problem?
Answer:
(8x
Tuesday, March 3, 2009

99. Example 3: Factor.
a. 64x2 - 81
8x · 8x 9 · 9
Check to see if the first and last terms are perfect squares.
Is it a subtraction problem?
Answer:
(8x (8x
Tuesday, March 3, 2009

100. Example 3: Factor.
a. 64x2 - 81
8x · 8x 9 · 9
Check to see if the first and last terms are perfect squares.
Is it a subtraction problem?
Answer:
(8x 9)(8x
Tuesday, March 3, 2009

101. Example 3: Factor.
a. 64x2 - 81
8x · 8x 9 · 9
Check to see if the first and last terms are perfect squares.
Is it a subtraction problem?
Answer:
(8x 9)(8x 9)
Tuesday, March 3, 2009

102. Example 3: Factor.
a. 64x2 - 81
8x · 8x 9 · 9
Check to see if the first and last terms are perfect squares.
Is it a subtraction problem?
Answer:
(8x + 9)(8x 9)
Tuesday, March 3, 2009

103. Example 3: Factor.
a. 64x2 - 81
8x · 8x 9 · 9
Check to see if the first and last terms are perfect squares.
Is it a subtraction problem?
Answer:
(8x + 9)(8x - 9)
Tuesday, March 3, 2009

104. Example 3: Factor.
b. r2 - 121 c. y2 + 100
e. x4 - 16
d. 25x4y6 - 36z8
Tuesday, March 3, 2009

105. Example 3: Factor.
b. r2 - 121 c. y2 + 100
( )( )
e. x4 - 16
d. 25x4y6 - 36z8
Tuesday, March 3, 2009

106. Example 3: Factor.
b. r2 - 121 c. y2 + 100
(r )( r )
e. x4 - 16
d. 25x4y6 - 36z8
Tuesday, March 3, 2009

107. Example 3: Factor.
b. r2 - 121 c. y2 + 100
(r 11)( r 11)
e. x4 - 16
d. 25x4y6 - 36z8
Tuesday, March 3, 2009

108. Example 3: Factor.
b. r2 - 121 c. y2 + 100
(r +11)( r - 11)
e. x4 - 16
d. 25x4y6 - 36z8
Tuesday, March 3, 2009

109. Example 3: Factor.
b. r2 - 121 c. y2 + 100
(r +11)( r - 11) Cannot be factored
e. x4 - 16
d. 25x4y6 - 36z8
Tuesday, March 3, 2009

110. Example 3: Factor.
b. r2 - 121 c. y2 + 100
(r +11)( r - 11) Cannot be factored
Not a difference
e. x4 - 16
d. 25x4y6 - 36z8
Tuesday, March 3, 2009

111. Example 3: Factor.
b. r2 - 121 c. y2 + 100
(r +11)( r - 11) Cannot be factored
Not a difference
e. x4 - 16
d. 25x4y6 - 36z8
( )( )
Tuesday, March 3, 2009

112. Example 3: Factor.
b. r2 - 121 c. y2 + 100
(r +11)( r - 11) Cannot be factored
Not a difference
e. x4 - 16
d. 25x4y6 -36z8
(5x2y3 )(5x2y3 )
Tuesday, March 3, 2009

113. Example 3: Factor.
b. r2 - 121 c. y2 + 100
(r +11)( r - 11) Cannot be factored
Not a difference
e. x4 - 16
d. 25x4y6
- 36z8
(5x2y3 6z4)(5x2y3 6z4 )
Tuesday, March 3, 2009

114. Example 3: Factor.
b. r2 - 121 c. y2 + 100
(r +11)( r - 11) Cannot be factored
Not a difference
e. x4 - 16
d. 25x4y6
- 36z8
(5x2y3+ 6z4)(5x2y3 - 6z4 )
Tuesday, March 3, 2009

115. Example 3: Factor.
b. r2 - 121 c. y2 + 100
(r +11)( r - 11) Cannot be factored
Not a difference
e. x4 - 16
d. 25x4y6
- 36z8
(5x2y3+ 6z4)(5x2y3 - 6z4 ) ( )( )
Tuesday, March 3, 2009

116. Example 3: Factor.
b. r2 - 121 c. y2 + 100
(r +11)( r - 11) Cannot be factored
Not a difference
e. x4 - 16
d. 25x4y6
- 36z8
(5x2y3+ 6z4)(5x2y3 - 6z4 ) (x2 )( x2 )
Tuesday, March 3, 2009

117. Example 3: Factor.
b. r2 - 121 c. y2 + 100
(r +11)( r - 11) Cannot be factored
Not a difference
e. x4 - 16
d. 25x4y6
- 36z8
(5x2y3+ 6z4)(5x2y3 - 6z4 ) (x2 4)( x2 4 )
Tuesday, March 3, 2009

118. Example 3: Factor.
b. r2 - 121 c. y2 + 100
(r +11)( r - 11) Cannot be factored
Not a difference
e. x4 - 16
d. 25x4y6
- 36z8
(5x2y3+ 6z4)(5x2y3 - 6z4 ) (x2+ 4)( x2 - 4 )
Tuesday, March 3, 2009

119. Example 3: Factor.
b. r2 - 121 c. y2 + 100
(r +11)( r - 11) Cannot be factored
Not a difference
e. x4 - 16
d. 25x4y6
- 36z8
(5x2y3+ 6z4)(5x2y3 - 6z4 ) (x2+ 4)( x2 - 4 )
(x2 + 4)(x + 2)(x - 2)
Tuesday, March 3, 2009

120. Homework
Tuesday, March 3, 2009

121. Homework
p. 690 #1-12, 21, 22, 25
“You must be the change you want to see in the world” -
Mahatma Ghandi
Tuesday, March 3, 2009