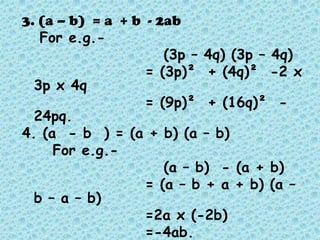The document provides an introduction to algebraic expressions, explaining fundamental concepts such as variables, terms, and the classification of expressions such as monomials, binomials, and trinomials. It details operations involving algebraic expressions, including multiplication and factorization, as well as rules for signs in division. Additionally, it offers historical context about the development of algebra and notable mathematicians who contributed to its evolution.

1. ALGEBRAIC
EXPRESSIONS

2. INTRODUCTION
• The rules in mathematics are called algebra.
Algebra is the grammar of math. The rules of
algebra tell how this equation can be formed and
changed.
Algebra is a way of thinking about arithmetic in a
general way. Instead of using specific numbers,
mathematicians have found that the easiest way
to write down the general rules of algebra is to
use what are called variables. Variables are
symbols (usually letters like a, b, x, y) that
represent either any number or an unknown
number. For example, one of the rules of algebra
says that a + b = b + a, where a and b are variables
that represent any numbers.

3. What is Algebraic
Expression?
• A number or a combination of numbers
connected by the symbols of operation
+,-,*,/ is called an algebraic
expression.
E.g.- 3x, 2x, -3/5x . The no’s 3, 2, -
3, -3/5 used above are constants and
the literal no’s x, y, z are variables.
The several parts are called terms.
The signs + and – connect the
different terms.
2x and -3y are terms of the

4. What are Monomial,
Binomial
and Trinomial?
An expression having only one term is
called monomial.
E.g.- 3x, -4y, 2/3yz are monomials.
An expression having two terns is called
binomial.
E.g.- 2x -3y, 4x + 5xz are
binomials.
An expression having three terms is
called trinomial.
E.g.- -3p + 5q -2/5pq, 7a - 2abc –

5. What are Like and Unlike
terms?
• Terms having same combinations of
literal numbers are called like terms.
• Terms do not having same combinations
of literal numbers are called unlike
terms.
For e.g.-
1. 4ab, -3ba = Like terms
2. 3xy, -5ya = Unlike terms
3. 6 abc, -5acd = Unlike terms
4. 8pq, -3qp = Like terms

6. What is Multiplication of
Algebraic Expressions?
• The product of two numbers of like signs is
positive and the product of two numbers of
unlike signs is negative.
For E.g., -
3 x 5 = 15; -4/5 x -5/3
= 4/3
-4 x 2 = -8; 3 x (-4/3) =
-4
We also know the following laws of
exponents
• a x a = a
• (a ) = a

7. What is Multiplication of a
Monomial by a Monomial?
• The product of two monomials is
obtained by the application of the
laws of exponents and the rules of
signs, e.g.,
• 2x y³ X 3x² y³ = (2x3) x X y
= 6x y
• Thus we have the following rules-
1. The numerical coefficient of the
product of two or more monomials is
equal to the product of their
numerical coefficients.
2. The variable part of the product

8. What is Multiplication of a
Binomial by a Monomial?
• To multiply a binomial by a monomial, we
use the following rule-
a x (b + c) = a x b + a x c
For E.g.-
Multiply: 4b + 6 by 3a
Product = 3a(4b + 6)
= 3a x 4b + 3a x 6
= 12ab + 18a

9. What is Multiplication of a
Trinomial by a Monomial?
To multiply a trinomial by a monomial,
we use the following rule:
a x (b + c + d) = a x b + a x c + a x d
For e.g. –
Multiply: 3x – 2x + 2 by 3x
Product = 3x(3x – 2x + 2)
= 3x x 3x – 3x x 2x
+ 3x x 2
= 9x² - 6x² + 6x

10. What is Multiplication of a
Polynomial by a
Polynomial?
• Let us multiply two binomials (4x – y) and
(3x – 2y). Here we will use the law of
multiplication of a binomial by a monomial
twice. Consider (4x – y) as one number.
Then (4x – y) (3x –
2y) = (4x –y) x 3 + (4x –y) x (-2y)
= 4x x 3x – y x 3x -4x x 2y
+ y x 2y
=12x² - 3xy – 8xy + 2y²
= 12x² - 11xy + 2y² .

11. Which are special Products
(Identities)?
The four special identities are:
1. (x + a) (x + b) = x + (a + b)x + ab
For e.g. –
(x + 3) (x + 2)
= x + (3 + 2)x + 3 x
2
= x + 5x + 6
2. (a + b) = a + b + 2ab
For e.g. –
(3p + 4q) (3p + 4q)
= (3p)² + (4q)² + 2
x 3p x 4q
= 9p² + (16q)² +

12. 3. (a – b) = a + b - 2ab
For e.g.-
(3p – 4q) (3p – 4q)
= (3p)² + (4q)² -2 x
3p x 4q
= (9p)² + (16q)² -
24pq.
4. (a - b ) = (a + b) (a – b)
For e.g.-
(a – b) - (a + b)
= (a – b + a + b) (a –
b – a – b)
=2a x (-2b)
=-4ab.

13. What are rules of signs in
Division?
1. When the dividend and the divisor have
the same signs, the quotient has the plus
sign.
2. When the dividend and the divisor have
opposite signs, the quotient has the
negative sign.
3. The process of division may be divided in
three cases:
• Division of a monomial by another
monomial.
• Division of a polynomial by monomial.
• Division of polynomial by another
polynomial.

14. What is Factorization of
Algebraic Expressions?
The factors of-
• a+ 2ab + b are (a+b) (a+b)
• A – 2ab + b are (a-b) (a-b)
• A -b are (a-b) (a +b)
• 4x are-
1. 4 X x²
2. 2 X 2 X x²
3. 2 X 2 X x X x
4. 4 X x X x
• 1 is a factor of every algebraic term, so 1 is
called a trivial factor.

15. How do we do Factorization by
Regrouping Terms?
• Sometimes it is not possible to find the
greatest common factor of the given set of
monomials. But by regrouping the given
terms, we can find the factors of the given
expression.
For e.g.,-
3xy + 2 + 6y + x = 3xy + 6y + x +
2
= 3y(x +
2) + 1(x + 2)
=(x + 2)

16. Some Other Information-
• The word algebra comes from the title of a
book on mathematics written in the early
800s by an Arab astronomer and
mathematician named al-Khwarizmi. The
rules of algebra are older than that,
however. The ancient Greeks wrote down
some of the rules that make up algebra, but
others came later. In the 500s Hindu
mathematicians in India added the idea of 0.
One of the final steps in the development of
modern algebra came in the 1600s, when
mathematicians developed the idea of
negative numbers. Although the ancient
Chinese and others had a way to indicate
negative numbers, it was not until the 1600s
that they were properly understood.

17. Made by : Samyak Jain- 04