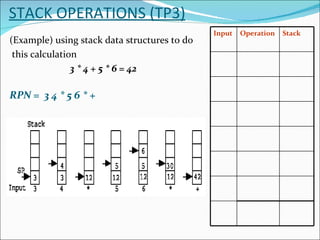
The document provides an overview of a computing lesson on Reverse Polish Notation (RPN) and use of the stack data structure. It includes the following key points: 1) Objectives are to review RPN concepts, apply RPN to the stack data structure, and review past paper questions. 2) Examples are provided to demonstrate converting infix expressions to postfix RPN and using a stack to evaluate RPN expressions step-by-step. 3) A worksheet exercise is assigned for students to complete, showing their working out. 4) The lesson aims to help students understand where RPN is applied, the differences between infix, prefix and postfix notation, and how RPN relates to the

1. Minster School Computing Reverse Polish Notation Part 2 Mr P Stevens [email_address]

2. Objectives Review key concepts from earlier RPN theory Apply RPN theory to the Stack Data Structure Review past paper RPN questions Review some aspects of the recent test

3. Convert to RPN Review (TP1) Convert the following expressions to RPN A * B + C * D  5 + ((1 + 2) * 4) − 3 

4. Convert to RPN Review Convert the following expressions to RPN A * B + C * D  AB*CD*+ 5 + ((1 + 2) * 4) − 3  12+4*5+3-

5. The Stack (A Reminder TP2) The Stack is LIFO To remove an item from the Stack we use the _________ command To place an item on the stack we use the __________ command

6. STACK OPERATIONS (TP3) (Example) using stack data structures to do this calculation 3 * 4 + 5 * 6 = 42 RPN = 3 4 * 5 6 * + Stack Operation Input

7. STACK OPERATIONS (Example) using stack data structures to do this calculation 3 * 4 + 5 * 6 = 42 RPN = 3 4 * 5 6 * + 12, 30 Pop 6,5 Multiply Push 30 12 Pop 4,3 Multiply Push 12 12, 5 Push 5 5 12, 5, 6 Push 6 6 42 Pop 30, 12 Add Push 42 3, 4 Push 4 4 3 Push 3 3 Stack Operation Input

8. Exercise Complete exercise 2 from the worksheet 2 Show your working out neatly

9. Plenary Objectives Understand where Polish form notation is applied Understand the terms Infix, Prefix and Postfix Convert expressions into RPN to produce postfix RPN expressions Appreciate how this theory is applied to the stack register Appreciate the role of Binary Tree Structures with RPN Review past paper RPN questions All resources available on the VLE! Test Paper Review