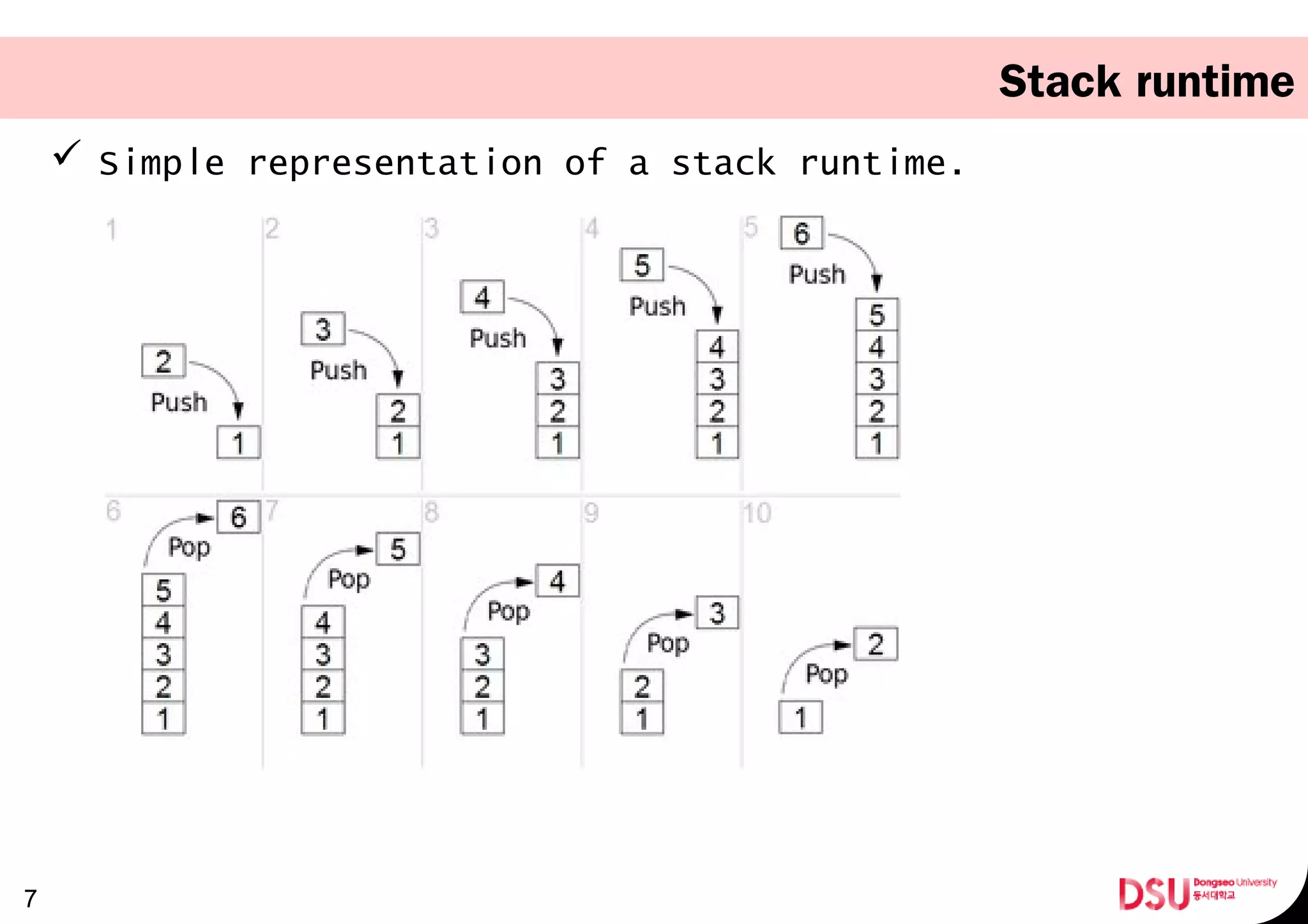
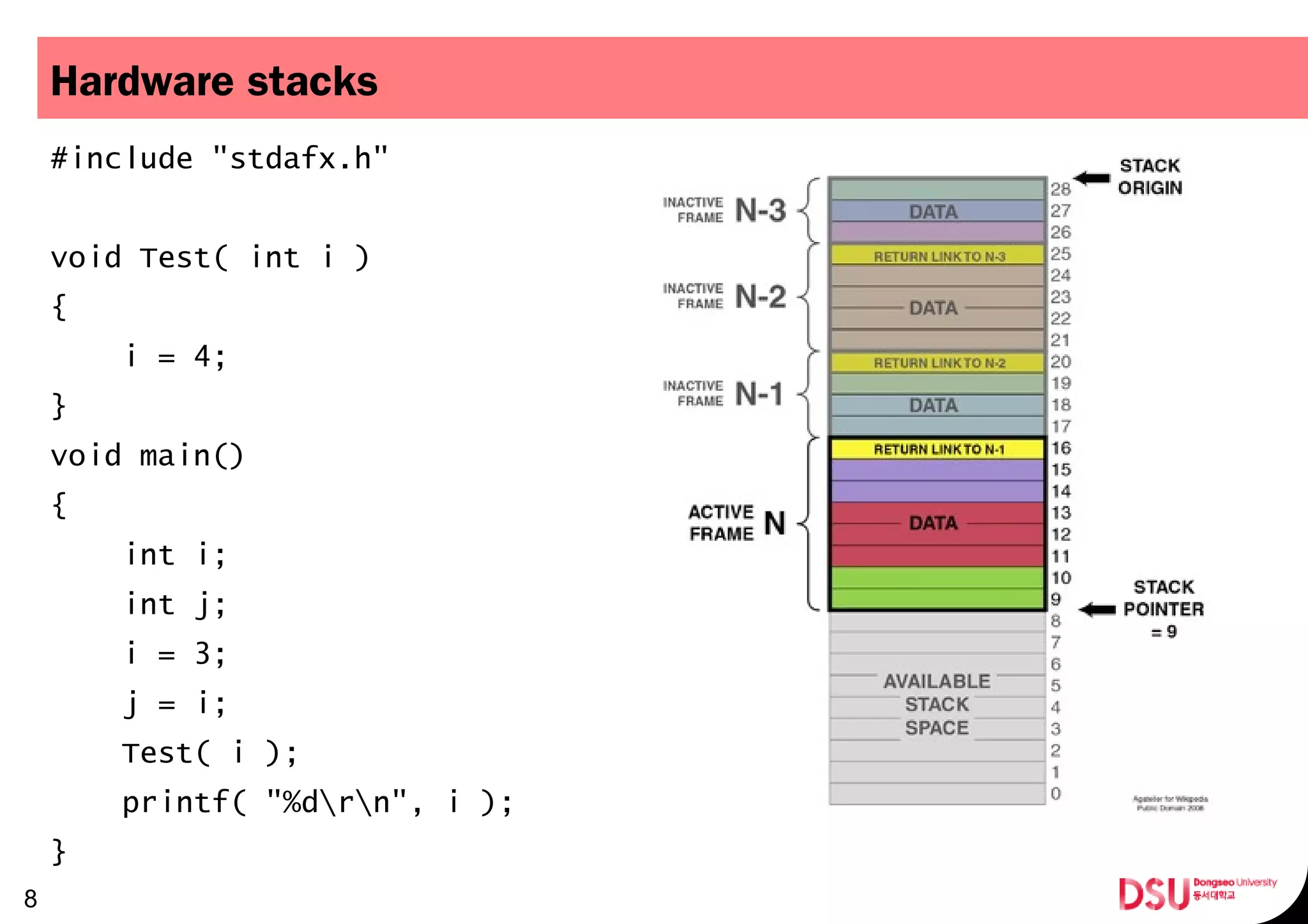
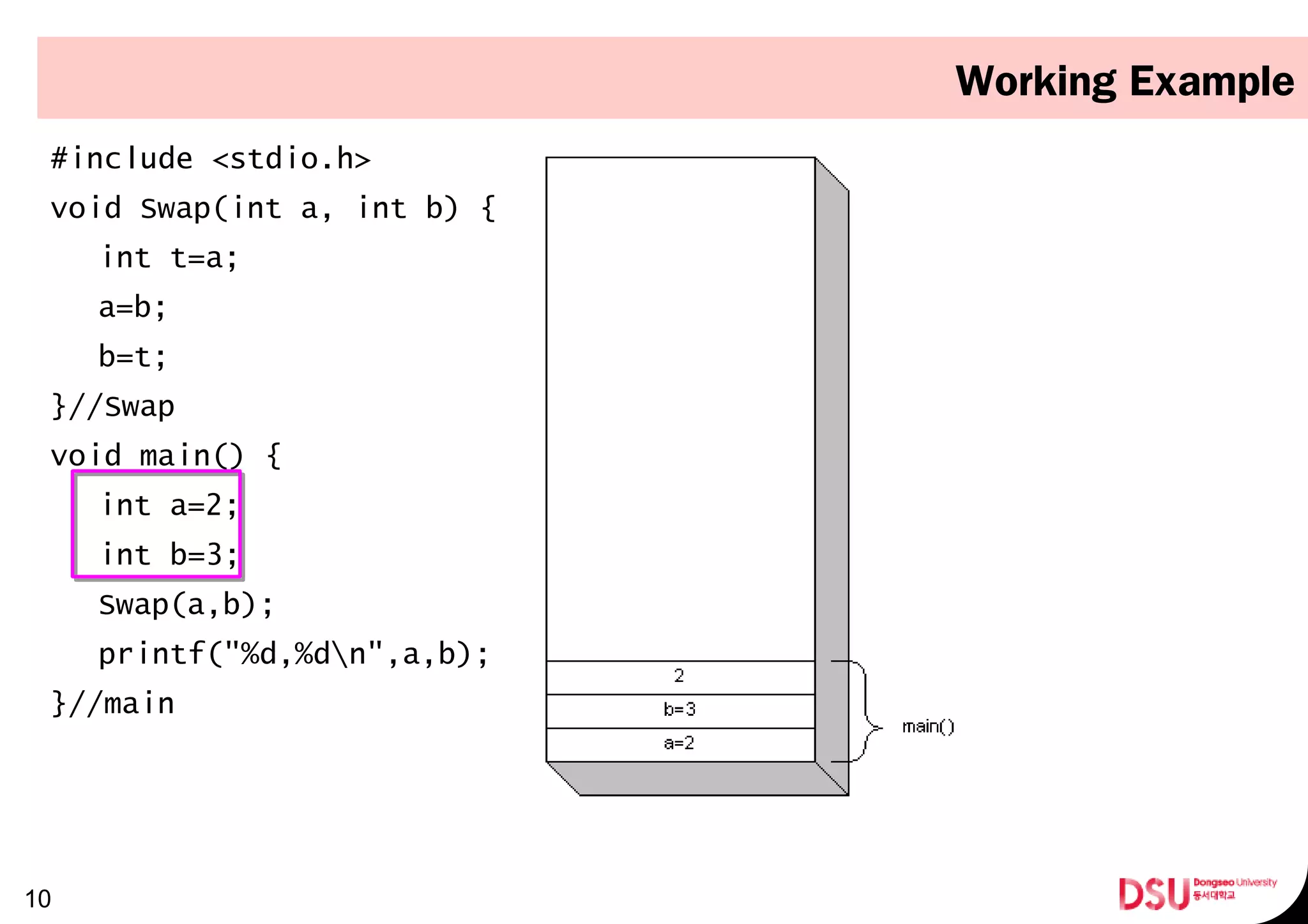
The document outlines a presentation on mobile game programming and stacks. It discusses abstract data types (ADTs), data structures, and specifically focuses on stacks. It provides examples of stack implementations in C++ using classes and templates. Finally, it discusses algorithms that use stacks, including converting number systems, evaluating postfix notation, and converting infix to postfix notation.

1. StackStack
Mobile Game ProgrammingMobile Game Programming
jintaeks@gmail.com
Division of Digital Contents, Dongseo Univ.
September 8, 2016

2. Presentation Outline
 ADT
 Data Structure
 Stack
 Implementation of a stack
– KStack
– template KStack
 Algorithms with stack
– Base conversion of numeral system
– Evaluation of postfix notation
– Conversion from infix to postfix notation
2

3. Abstract Data Type(ADT)
 an abstract data type ( ADT) is a mathematical model for
data types where a data type is defined by its behavior
(semantics) from the point of view of a user of the
data.
 possible values, possible operations on data of this
type, and the behavior of these operations.
 Example: integers
– Values …, -2, -1, 0, 1, 2, …
– Operations
• Addition
• Subtraction
• Multiplication
• Division
• Greater than, etc…
3

4. ADT examples
 Some common ADTs, which have proved useful in a great
variety of applications, are:
– Container, List, Set, Multiset
– Map, Multimap, Graph, Stack
– Queue, Priority queue
– Double-ended queue
– Double-ended priority queue
4

5. Data Structure(s)
 a data structure is a particular way of organizing data in
a computer so that it can be used efficiently.
 Data Structures implement one or more particular
abstract data types (ADT).
 Data Structure is a concrete implementation of the
contract provided by an ADT.
 Examples:
– Array, Stack, List
– Associative array, Record(struct)
– Union
– Set
– Graph, Tree
– Class
– …
5

6. Stack
 an abstract data type that serves as a collection of
elements.
 two principal operations:
– push, which adds an element to the collection.
– pop, which removes the most recently added element that was
not yet removed.
 LIFO (for last in, first out)
 the push and pop operations occur only at one end of
the structure, referred to as the top of the stack.
 may be implemented to have a bounded capacity.
 Overflow
– when the stack is full and does not contain enough space to
accept an entity to be pushed.
6

7. Stack runtime
 Simple representation of a stack runtime.
7

8. Hardware stacks
#include "stdafx.h"
void Test( int i )
{
i = 4;
}
void main()
{
int i;
int j;
i = 3;
j = i;
Test( i );
printf( "%drn", i );
}
8

9. Stack Settings in Visual Studio 2013
 Property pageLinkerSystemStack Reserve Size
9

10. Working Example
#include <stdio.h>
void Swap(int a, int b) {
int t=a;
a=b;
b=t;
}//Swap
void main() {
int a=2;
int b=3;
Swap(a,b);
printf("%d,%dn",a,b);
}//main
10

11. #include <stdio.h>
void Swap(int a, int b) {
int t=a;
a=b;
b=t;
}//Swap
void main() {
int a=2;
int b=3;
Swap(a,b);
printf("%d,%dn",a,b);
}//main
11

12. #include <stdio.h>
void Swap(int a, int b) {
int t=a;
a=b;
b=t;
}//Swap
void main() {
int a=2;
int b=3;
Swap(a,b);
printf("%d,%dn",a,b);
}//main
12

13. #include <stdio.h>
void Swap(int a, int b) {
int t=a;
a=b;
b=t;
}//Swap
void main() {
int a=2;
int b=3;
Swap(a,b);
printf("%d,%dn",a,b);
}//main
13

14. Revised working example
#include <stdio.h>
void Swap(int *a,int *b) {
int t=*a;//assigns the contents of a to t
*a=*b;//assigns the contents of b to the location of contents of
a.
*b=t;//assigns the t to the location of contents of b
}//Swap
void main() {
int a=2,b=3;
Swap(&a,&b);//pass addresses of a and b
printf("%d,%dn",a,b);
}//main
14

15. 15
#include <stdio.h>
void Swap(int *a,int *b) {
int t=*a;//assigns the contents of a to t
*a=*b;//assigns the contents of b to the location of contents of
a.
*b=t;//assigns the t to the location of contents of b
}//Swap
void main() {
int a=2,b=3;
Swap(&a,&b);//pass addresses of a and b
printf("%d,%dn",a,b);
}//main

16. 16
#include <stdio.h>
void Swap(int *a,int *b) {
int t=*a;//assigns the contents of a to t
*a=*b;//assigns the contents of b to the location of contents of
a.
*b=t;//assigns the t to the location of contents of b
}//Swap
void main() {
int a=2,b=3;
Swap(&a,&b);//pass addresses of a and b
printf("%d,%dn",a,b);
}//main

17. 17
#include <stdio.h>
void Swap(int *a,int *b) {
int t=*a;//assigns the contents of a to t
*a=*b;//assigns the contents of b to the location of contents of
a.
*b=t;//assigns the t to the location of contents of b
}//Swap
void main() {
int a=2,b=3;
Swap(&a,&b);//pass addresses of a and b
printf("%d,%dn",a,b);
}//main

18. 18
#include <stdio.h>
void Swap(int *a,int *b) {
int t=*a;//assigns the contents of a to t
*a=*b;//assigns the contents of b to the location of contents of
a.
*b=t;//assigns the t to the location of contents of b
}//Swap
void main() {
int a=2,b=3;
Swap(&a,&b);//pass addresses of a and b
printf("%d,%dn",a,b);
}//main

19. C++ implementations of a stack
class KStack
{
public:
KStack() : m_sp( 0 )
{
}
void Push( int data_ );
bool Pop( int& outData_ );
bool IsEmpty() const;
private:
int m_sp;
int m_data[ 100 ];
};//class KStack
19

20. void KStack::Push( int data_ )
{
m_data[ m_sp ] = data_;
m_sp += 1;
}
bool KStack::Pop( int& outData_ )
{
if( m_sp <= 0 ) return false;
m_sp -= 1;
outData_ = m_data[ m_sp ];
return true;
}
bool KStack::IsEmpty() const
{
return m_sp == 0;
}20

21. Template KStack
template<typename T, int STACK_SIZE>
class KStack
{
public:
KStack() : m_sp( 0 )
{
}
void Push( T data_ );
bool Pop( T& outData_ );
bool IsEmpty() const;
private:
int m_sp;
T m_data[ STACK_SIZE ];
};//class KStack
21

22. template<typename T, int STACK_SIZE>
void KStack<T,STACK_SIZE>::Push( T data_ )
{
m_data[ m_sp ] = data_;
m_sp += 1;
}
template<typename T, int STACK_SIZE>
bool KStack<T, STACK_SIZE>::Pop( T& outData_ )
{
if( m_sp <= 0 ) return false;
m_sp -= 1;
outData_ = m_data[ m_sp ];
return true;
}
22

23. void main()
{
KStack<int,100> s;
s.Push( 3 );
s.Push( 5 );
int data;
const bool bIsPop = s.Pop( data );
printf( "%drn", data );
}
23

24. Actual usage of stack in C++
 std::stack
template<
class T,
class Container = std::deque<T>
> class stack;
 a container adapter that gives the programmer the
functionality of a stack - specifically, a LIFO (last-
in, first-out) data structure.
24

25. #include <stack>
void main()
{
std::stack<int> s;
int n;
printf( "Enter decimal digit:" );
scanf( "%d", &n );
while( n >= 5 )
{
s.push( n % 5 );
n /= 5;
}//while
25
printf( "Equivalent Quintett
is %d", n );
while( s.empty() == false )
{
n = s.top();
printf( "%d", n );
s.pop();
}//while
}//main

26. Algorithms with Stack
 Convert Decimal Number to Pentamal Number
 Reverse Polish Notation: Evaluating Postfix Notation
 Conversion from Infix to Postfix Notation
26

27. Convert Decimal Number to Pentamal Number
 divide the number by 5.
 write quotient and remainder.
 now quotient is dividend, continue till dividend is
less than 5.
27

28. void main()
{
KStack<int, 100> s;
int n;
printf( "Enter decimal number:" );
scanf( "%d", &n );
while( n >= 5 )
{
s.Push( n % 5 );
n /= 5;
}//while
printf( "Equivalent pentamal is ", n );
while( s.Pop( n ) )
printf( "%d", n );
}//main28

29. Practice
 Write a class that convert decimal number to n-ary
number.
– binary
– trimal
– tetramal
– pentamal
– hexamal
– heptamal
– octal
– nonamal
 there must a getter that gets the converted number in
string.
29

30. Reverse Polish Notation: Postfix Notation
 the operators follow their operands;
 for instance, to add 3 and 4, one would write "3 4 +"
rather than "3 + 4".
 "3 4 + 5“−  "3 4 5 +"−
– if there are multiple operations, the operator is given
immediately after its second operand.
 it removes the need for parentheses that are required
by infix.
 "3 (4 × 5)“ is quite different from "(3 4) × 5".− −
 In postfix, it could be written "3 4 5 × ", which−
unambiguously means "3 (4 5 ×) " which reduces to "3−
20 “.−
30

31. Evaluation postfix expression
 While there are input tokens left
– Read the next token from input.
– If the token is a value
• Push it onto the stack.
– Otherwise, the token is an operator (operator here includes
both operators and functions).
• It is known a priori that the operator takes n arguments.
• If there are fewer than n values on the stack
– (Error) The user has not input sufficient values in the expression.
• Else, Pop the top n values from the stack.
• Evaluate the operator, with the values as arguments.
• Push the returned results, if any, back onto the stack.
 If there is only one value in the stack
– That value is the result of the calculation.
 Otherwise, there are more values in the stack
– (Error) The user input has too many values.
31

32. example: "5 + ((1 + 2) × 4) 3“−  5 1 2 + 4 × + 3 −
32
Input Operation Stack Comment
5 Push 5
1
Push 1
5
2
Push 2
1
5
+
Add 3
Pop two values (1, 2) and push result (3)
5
4
Push 4
3
5
×
Multiply 12
Pop two values (3, 4) and push result (12)
5
+ Add 17Pop two values (5, 12) and push result (17)
3
Push value 3
17
− Subtract 14Pop two values (17, 3) and push result (14)
Result 14

33. Practice
 Write a class that evaluates a postfix notation.
33

34. Conversion from Infix to Postfix Notation
While there are tokens to be read:
•Read a token.
•If the token is a number, then add it to the output
queue.
•If the token is an operator, o1, then:
• while there is an operator token o2, at the top of the
operator stack and either
• o1 is left-associative and its precedence is less than or
equal to that of o 2, or
• o1 is right associative, and has precedence less than that of
o2,
• pop o2 off the operator stack, onto the output queue;
• at the end of iteration push o1 onto the operator stack.
•If the token is a left parenthesis (i.e. "("), then push
it onto the stack.34

35. • If the token is a left parenthesis (i.e. "("), then
push it onto the stack.
• If the token is a right parenthesis (i.e. ")"):
• Until the token at the top of the stack is a left
parenthesis, pop operators off the stack onto the output
queue.
• Pop the left parenthesis from the stack, but not onto the
output queue.
• If the stack runs out without finding a left parenthesis,
then there are mismatched parentheses.
When there are no more tokens to read:
• While there are still operator tokens in the stack:
• If the operator token on the top of the stack is a
parenthesis, then there are mismatched parentheses.
• Pop the operator onto the output queue.
Exit.35

36. Detailed example: 3 + 4 * 2 / ( 1 - 5 ) ^ 2 ^ 3
 predefined operator properties table.
 How can we implement this properties table?
36

37. Detailed example: 3 + 4 * 2 / ( 1 - 5 ) ^ 2 ^ 3
37

38. Detailed example: 3 + 4 * 2 / ( 1 - 5 ) ^ 2 ^ 3
38

39. Practice
 Write a class that converts Infix notation to Postfix
notation.
 Expand the features of existing class(written in
previous learning).
39

40. int priority( char a ) {
int temp = 0;
if( a == '^' )
temp = 4;
else if( a == '*' || a == '/' )
temp = 3;
else if( a == '+' || a == '-' )
temp = 2;
return temp;
}
int main() {
std::string infix;
infix = "3+4*2/(1-5)^2^3";
std::stack<char> operator_stack;
std::string postfix;
40

41. for( unsigned i = 0; i < infix.length(); i++ ) {
if( infix[ i ] == '+' || infix[ i ] == '-' || infix[ i ] == '*' || infix[
i ] == '/' ) {
//
} else if( infix[ i ] == '^' ) {
//
} else if( infix[ i ] == '(' ) {
operator_stack.push( infix[ i ] );
} else if( infix[ i ] == ')' ) {
while( operator_stack.top() != '(' ) {
postfix += operator_stack.top();
operator_stack.pop();
}
operator_stack.pop();
} else {
postfix += infix[ i ];
}
}
41

42. if( infix[ i ] == '+' || infix[ i ] == '-' || infix[ i ] == '*' || infix[ i ] == '/'
) {
while( !operator_stack.empty() && priority( infix[ i ] ) <=
priority( operator_stack.top() ) ) {
postfix += operator_stack.top();
operator_stack.pop();
}
operator_stack.push( infix[ i ] );
} else if( infix[ i ] == '^' ) {
while( !operator_stack.empty() && priority( infix[ i ] ) <
priority( operator_stack.top() ) ) {
postfix += operator_stack.top();
operator_stack.pop();
}
operator_stack.push( infix[ i ] );
} else if( infix[ i ] == '(' ) {
42

43. while( !operator_stack.empty() ) {
postfix += operator_stack.top();
operator_stack.pop();
}//while
std::cout << postfix << std::endl;
return 0;
}
43

44. Actual usage of equation evaluation in C++
 boost::math
 boost::spirit
44

45. End
 https://en.wikipedia.org/wiki/Abstract_data_type
 https://en.wikipedia.org/wiki/Reverse_Polish_notation
 https://en.wikipedia.org/wiki/Shunting-yard_algorithm
 http://www.cplusplus.com/forum/beginner/16722/
45