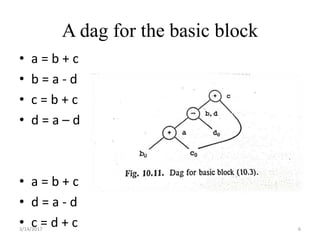
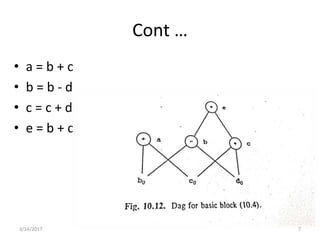
The document discusses various optimization techniques that can be applied to basic blocks in code including: - Common subexpression elimination and dead code elimination to remove redundant computations. - Algebraic transformations like applying arithmetic identities to simplify expressions and reduce strength of operations. - Representing the basic block as a directed acyclic graph (DAG) to help identify common subexpressions and apply transformations using properties like commutativity.

1. OPTIMIZATION OF BASIC
BLOCKS
ISHWARYA LAKSHMI.TK
BP150516
3/14/2017 1

2. OPTIMIZATION OF BASIC BLOCKS
• The code improving transformations for basic
blocks included structure - preserving
transformations, such as common sub
expression elimination and dead-code
elimination, and algebraic transformation such
as reduction in strength.
3/14/2017 2

3. Cont …
• Many of the structure-preventing
transformation can be implemented by
constructing a dag or a basic blocks
• Recall that there is a node in the dag for each
of the initial values of the variables appearing
in the basic block, and there is a node n
associated with each statement s within the
block.
3/14/2017 3

4. Cont …
• Node n is labeled by the operator applied at s,
and also attached to n is the list of variables for
which it is the last definition within the block.
• If any node’s values are live on exit from the
block, these are the output nodes.
3/14/2017 4

5. Cont …
• Common sub expressions can be detected by
noticing, as a new node m is about to a added,
whether there is an existing node n with the
same children, in the same order, and with the
same operator. If so, n computes the same
value as m and may be used in its place.
3/14/2017 5

6. A dag for the basic block
• a = b + c
• b = a - d
• c = b + c
• d = a – d
• a = b + c
• d = a - d
• c = d + c3/14/2017 6

7. Cont …
• a = b + c
• b = b - d
• c = c + d
• e = b + c
3/14/2017 7

8. The Use of Algebraic Identities
• Algebraic identities another important class of
optimization on basic blocks.
• The simple algebraic transformations that one
might try during optimization.
• For examples apply arithmetic identities, such
as
• x + 0 = 0 + x = x
• x – 0 = x
• x * 1 = 1 * x = x
• x / 1 =x
3/14/2017 8

9. Cont …
• Another class of algebraic optimization
includes reduction in strength, that is,
replacing a more expensive operator by a
cheaper one as in
• x * * 2 = x * x
• 2.0 * x = x + x
• x / 2 = x * 0.5
3/14/2017 9

10. Cont …
• Evaluate constant expressions at compile time
and replace the constant expressions by their
values.
– 2*3.14 => 6.28
• The dag-construction process can help us
apply these and other more general algebraic
transformations such as commutative and
associative
3/14/2017 10

11. Cont …
• For example, suppose * is commutative ; that
is, x * y = y * x.
• Before create a new node labeled * with left
child m and right child n, check whether such
a node already exists, then check for a node
having operator *, let child n and right child m.
3/14/2017 11

12. Cont …
• The relational operators <=, >=, <, >, =, and !=
sometimes generate unexpected common sub
expressions.
• For example
• X – y and x > y
3/14/2017 12

13. Cont …
• Associative laws may also be applied to
expose common sub expressions.
• For example
• a = b + c
• e = c + d +b
Intermediate node generated
• a = b + c
• t = c + d -> a = b + c
• e = t + b -> e = a + d
3/14/2017 13

14. Cont …
• Computer arithmetic does not always the
algebraic identities o mathematics.
• For example, the standard for Fortran77 states
that a integrity of parentheses is not violated.
• Thus, a compiler may evaluate x * y – x * z as
x*(y-z) but it may not evaluate a + ( b – c ) as
( a + b ) - c.
3/14/2017 14