Overlapping correlation clustering

overlapping correlation clustering
francesco bonchi
aris gionis
antti ukkonen

yahoo! research barcelona

Monday, September 26, 2011

overlapping clusters are very natural

- social networks

- proteins

- documents

2

most clustering algorithms produce
disjoint partitions

3

overlapping is conceptually challenging to
formulate

- why assign a point to a further center?

- why/how to generate less good clusters?

4

correlation clustering

Ccc () = |s(u, v) − I((u) = (v))|

5

1

7

0

8

0.33
???

9

0.33

10

0.33

multiple labels = multi-cluster assignment

10

0.5

11

0.67

12

54167/108301
???

13

overlapping correlation clustering

Cocc () = |s(u, v) − H((u), (v))|

14

comparing sets of labels H((u), (v))

- Jaccard coefﬁcient

- set intersection indicator

15

overlapping
correlation clustering correlation clustering

16

overlapping

set of labels L, |L| = k

16

overlapping


(u) ∈ L (u) ⊆ L

16

overlapping


(u) ∈ L (u) ⊆ L

C() = |s(u, v) − H((u), (v))|

16

overlapping


(u) ∈ L (u) ⊆ L

C() = |s(u, v) − H((u), (v))|

|(u)| ≤ p

16

dimensionality reduction

- mapping to sets instead of vectors

17

v

u
y
x

19

v

u
y
x (u,v)

(x,y)

19

u∈V {v}

expresses the error incurred by vertex v when it has the labels Now, giv
(v), and the remaining nodes are labeled according to . The J(X, Sj
subscript p in Cv,p serves to remind us that the set (v) should
have at most p labels. Our general local-search strategy is
summarized in Algorithm 1.

Algorithm 1 LocalSearch which is
1: initialize to a valid labeling;
2: while Cocc (V, ) decreases do
3: for each v ∈ V do
and we
4: find the label set L that minimizes Cv,p (L | );
We obse
5: update so that (v) = L;
to the un
6: return
xi and t
Equation
Line 4 is the step in which LocalSearch seeks to find an
propose
optimal set of labels for an object v by solving Equation (3).
constrain
This is also the place that our framework differentiates be-
squares
tween the measures of Jaccard coefficient and set-intersection.
optimiza
B. Local step for Jaccard coefficient variables
Problem 3 (JACCARD - TRIANGULATION): Consider the set20 The s
{S , z }
, where S are subsets of a ground set U = drawbac

Jaccard triangulation

given {Sj , zj }j=1...n

ﬁnd X ⊆ U

to minimize
n

d(X, {Sj , zj }j=1...n ) = |J(X, Sj ) − zj |
j=1

21

set-intersection indicator

hit-n-miss sets
√
O( n log n) approximation

greedy approach

22

experimental evaluation

23

EMOTION: 593 objects, 6 labels

YEAST: 2417 objects, 14 labels

24

EMOTION YEAST
0.2 1 0.2 1

Precision Recall

Precision Recall
Cost/edge

Cost/edge
cost cost
0.1 prec 0.8 0.1 prec 0.9
rec rec

0 0.6 0 0.8
2 4 6 8 10 5 10 15 20
k k
EMOTION YEAST F
0.1 1 1
r

Precision Recall

Precision Recall
I
Cost/edge

Cost/edge
cost 0.1 cost
prec 0.5 prec 0.9
rec rec c
p
d
0 0 0 0.8
2
p
4 6 2 4 6
p
8 10 12 14 s
t
Fig. 1. Cost per edge, precision and recall of OCC-JACC as a function of
25

EMOTION YEAST
0.05 0.6 0.04 1

Precision Recall

Precision Recall
0.4
Cost/edge

Cost/edge
cost cost
prec 0.03 prec
rec 1 rec

0.8
0 0.02 0.8
0.01 0.02 0.03 0.04 0.01 0.02 0.03 0.04
q q

Fig. 3. Pruning experiment using OCC-JACC. Cost/edge and precision and
recall as a function of the pruning threshold q.

In fact, the results for YEAST shown in ﬁgures 1 and 2 were
26
computed with q = 0.05. In terms of computational speedup

protein clustering

- pairwise similarities based on matching of
amino-acid sequences

- compare using a hand-made taxonomy

27

TABLE II
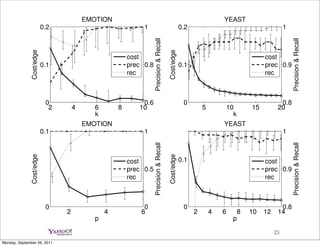
Precision, recall, and their harmonic mean F-score, for non-overlapping C
non-overlapping
clusterings of protein sequence datasets computed using SCPS [14] and the
OCC algorithms. BL is the precision of a baseline that assigns all
sequences to the same cluster.

BL SCPS OCC-ISECT OCC-JACC
dataset prec prec/recall/F-score prec/recall/F-score prec/recall/F-score
D1 0.21 0.56 / 0.82 / 0.664 0.70 / 0.67 / 0.683 0.57 / 0.55 / 0.561
D2 0.17 0.59 / 0.89 / 0.708 0.86 / 0.83 / 0.844 0.64 / 0.63 / 0.637
D3 0.38 0.93 / 0.88 / 0.904 0.81 / 0.43 / 0.558 0.73 / 0.39 / 0.505
D4 0.14 0.30 / 0.64 / 0.408 0.64 / 0.56 / 0.598 0.44 / 0.39 / 0.412

Summarizing: C3 and C4 contain elks and deer that stay
away from cattle (C3 moving in higher X than C4 ); C1 also
contains only elks and deer, but those moves in the higher Y ex
area where also the cattles move; C2 is the cattle cluster and co
it contains also few elks and deer; ﬁnally C5 is another mixed be
cluster which overlaps with C2 only for the cattle and28with

overlapping
TABLE III
erlapping Comparing clusterings cost based on distance on the SCOP taxonomy, for
4] and the different values of p, the maximum number of labels per protein.
gns all
SCPS OCC-ISECT-p1 OCC-ISECT-p2 OCC-ISECT-p3
D1 0.231 0.196 0.194 0.193
OCC-JACC D2 0.188 0.112 0.107 0.106
call/F-score D3 0.215 0.214 0.214 0.231
.55 / 0.561 D4 0.289 0.139 0.133 0.139
.63 / 0.637 SCPS OCC-JACC-p1 OCC-JACC-p2 OCC-JACC-p3
.39 / 0.505
.39 / 0.412 D1 0.231 0.208 0.202 0.205
D2 0.188 0.137 0.130 0.127
D3 0.215 0.243 0.242 0.221
that stay D4 0.289 0.158 0.141 0.152
C1 also
higher Y extremely close in the taxonomy, the error should have a small
uster and cost. Following this intuition we deﬁne the SCOP similarity
er mixed between two proteins as follows:
and with d(lca(u, v))
sim(u, v) = , (8)
max(d(u), d(v)) − 1 29

future work

- scaling up

- approximation algorithm

- jaccard triangulation

- more experimentation and applications

30

thank you!


Overlapping correlation clustering

More Related Content

Recently uploaded

Featured

Overlapping correlation clustering