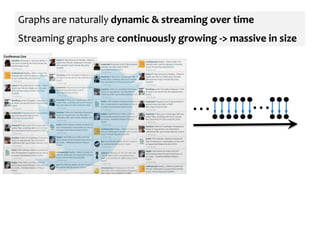
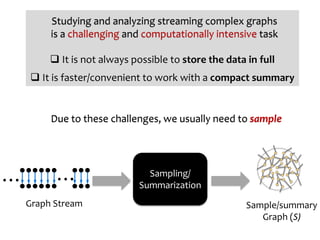
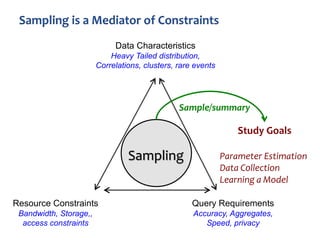
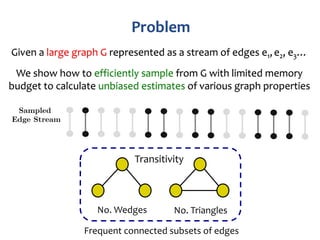
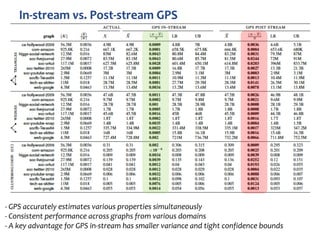
The document discusses advanced techniques for streaming graph analysis, focusing on sampling and unbiased estimation methods to handle massive dynamic graphs. It introduces a priority sampling framework that efficiently estimates various graph properties while addressing challenges such as computational feasibility and memory constraints. The work demonstrates the effectiveness of the proposed methods through real-world applications and empirical results.

1. Joint Work with:
Ryan RossiNick Duffield Ted willke

2. • Streaming Graph Algorithms
• Unbiased estimation, sketching, summarization, bipartite graph projection
• Relational Learning
• Sampling, inference, representation learning, graph embeddings, role discovery,
higher-order models, graph kernels, graph convolutions
• Parallel Graph Algorithms
• Subgraph counting, graphlet decomposition, approximations, coloring, kcore/ktruss
• Applications
• Real-time graph mining, interactive visual graph analytics, higher-order network
analysis, brain connectivity
Nesreen Ahmed – Intel Labs
Large-Scale Relational Learning & Graph Mining
Theory, Algorithms, and Applications
……

3. (1) Challenges for streaming graph analysis
(2) A framework for sampling/summarization of massive
streaming graphs

4. ⋯ ⋯
Graphs are naturally dynamic & streaming over time
Streaming graphs are continuously growing -> massive in size

5. ⋯ ⋯
t-p t-1 t
⋯
⋯
⋯
⋯
Graphs are naturally dynamic & streaming over time
Streaming graphs are continuously growing -> massive in size

6. t=1 t=2
[1, 5] [6, 10]
Discrete-time models: represent dynamic network as a sequence
of static snapshot graphs where
User-defined aggregation time-interval
Very coarse representation with
noise/error problems
Difficult to manage at a large scale
Streaming Model

7. Due to these challenges, we usually need to sample
Sampling/
Summarization
Studying and analyzing streaming complex graphs
is a challenging and computationally intensive task
q It is not always possible to store the data in full
q It is faster/convenient to work with a compact summary
⋯ ⋯
Sample/summary
Graph (S)
Graph Stream

8. Data/ML
Algorithms
Sample/summary
Graph (S)
Model Learning
Study Network
Structure
Network Parameter
Estimation
Feature Representation
.
.
.
Turn large data streams into smaller manageable data
- Speedup queries, analysis, and savings in storage
Approximate
Query Processing

9. § Other Alternatives
• Sketching
• dimensionality reduction
• dictionary-based summarization
All worthy of studying – but not the focus of this talk

10. § Sampling has an intuitive semantics
§ Statistical estimation on a sample is often straightforward
• Run the analysis on the sample that you would on the full data
• Some rescaling/reweighting may be necessary
§ Sampling is general/agnostic to the analysis to be done
• can be tuned to optimize some criteria
§ Sampling is (usually) easy to understand

11. Data Characteristics
Heavy Tailed distribution,
Correlations, clusters, rare events
Query Requirements
Accuracy, Aggregates,
Speed, privacy
Resource Constraints
Bandwidth, Storage,,
access constraints
Sampling
Study Goals
Parameter Estimation
Data Collection
Learning a Model
Sample/summary

12. Given a large graph G represented as a stream of edges e1,e2, e3…
We show how to efficiently sample from G with limited memory
budget to calculate unbiased estimates of various graph properties

13. Frequent connected subsets of edges
Transitivity
No. TrianglesNo. Wedges
Given a large graph G represented as a stream of edges e1,e2, e3…
We show how to efficiently sample from G with limited memory
budget to calculate unbiased estimates of various graph properties

14. § Take a single linear scan of the edge stream to draw a sample
• Streaming model of computation: see each element once
• Flip a coin with probability p for each edge
• If head, edge is added to the sample
• Variable sample size
• Problems with handling heavy-tailed distributions

15. “Reservoir sampling” described by [Knuth 69, 81]; enhancements
[Vitter 85]
§ Fixed size k uniform sample from arbitrary size N stream in one
pass
§ No need to know stream size in advance
§ Include first k items w.p. 1
§ Include item n > k with probability p(n) = k/n, n > k
— Pick j uniformly from {1,2,…,n}
— If j ≤ k, swap item n into location j in reservoir, discard
replaced item
Easy to prove the uniformity of the sampling method

16. § Single-pass algorithms for arbitrary-ordered graph streams
• Streaming-Triangles – [Jha et al. KDD’13]
— Sample edges using reservoir sampling, then sample pairs of incident
edges (wedges), and finally scan for closed wedges (triangles)
• Neighborhood Sampling – [Pavan et al. VLDB’13]
— Sampling vectors of wedge estimators, scan the stream for closed wedges
(triangles)
• TRIEST– [De Stefani et al. KDD’16]
— Uses standard reservoir sampling to maintain the edge sample
• MASCOT– [Lim et al. KDD’15]
— Bernoulli edge sampling with probability p
• Graph Sample & Hold– [Ahmed et al. KDD’14]
— Weighted conditionally independent edge sampling

17. Focus of previous work
Sampling designs for specific graph properties (triangles)
Not generally applicable to other properties
Uniform-based Sampling
Obtain variable-size sample

18. Focus of previous work
Sampling designs for specific graph properties (triangles)
Not generally applicable to other properties
Uniform-based Sampling
Obtain variable-size sample
Our focus - Graph Priority Sampling
• Weight-sensitive
• Fixed-size sample
• Single-pass
• Applicable for general graph properties
• Can incorporate auxiliary variables

19. (1) Challenges for streaming graph analysis
(2) A framework for sampling/summarization of massive
streaming graphs
✓
[Ahmed et al., VLDB 2017], [Ahmed et al., IJCAI 2018]

20. § Order sampling a.k.a. bottom-k sample, min-hashing
§ Uniform sampling of stream into reservoir of size k
§ Each arrival n: generate one-time random value rn Î U[0,1]
• rn also known as hash, rank, tag…
§ Store k items with the smallest random tags
§ Each item has same chance of least tag, so still uniform
0.391 0.908 0.291 0.555 0.619 0.273

21. Input
Graph Priority Sampling Framework
GPS(m)
Output
Edge stream
k1, k2, ..., k, ...
Sampled Edge stream ˆK
Stored State m = O(| ˆK|)

22. Input
Graph Priority Sampling Framework
GPS(m)
Output
For each edge k
Generate a random number
u(k) ⇠ Uni(0, 1]
Edge stream
k1, k2, ..., k, ...
Sampled Edge stream ˆK
Stored State m = O(| ˆK|)
Compute edge weight
w(k) = W(k, ˆK)
Compute edge priority
r(k) = w(k)/u(k)
ˆK = ˆK [ {k}

23. Input
Graph Priority Sampling Framework
GPS(m)
Output
For each edge k
Edge stream
k1, k2, ..., k, ...
Sampled Edge stream ˆK
Stored State m = O(| ˆK|)
Find edge with lowest priority
k⇤
= arg mink02 ˆK r(k0
)
Update sample threshold
z⇤
= max{z⇤
, r(k⇤
)}
Remove lowest priority edge
ˆK = ˆK{k⇤
}
Use a priority queue with O(log m) updates

24. § We use edge weights to express the role of the arriving
edge in the sample/summary graph
• e.g., subgraphs completed by the arriving edge
• other auxiliary variables
§ Computational feasibility
• Efficient implementation by using a priority queue
• Implemented as a Min-heap with O(log m) insertion/deletion
• O(1) access to the edge with minimum priority
w(k) = W(k, ˆK)
Compute edge priority
r(k) = w(k)/u(k)

25. For each edge i,
we construct a sequence of edge estimators ˆSi,t
We achieve unbiasedness by
establishing that the sequence is a Martingale (Theorem 1)
E[ ˆSi,t] = Si,t
ˆSi,t = I(i 2 ˆKt)/min{1, wi/z⇤
}
where ˆSi,t are unbiased estimators of the corresponding edge
ˆKt is the sample at time t
Edge Estimation
[Ahmed et al, VLDB 2017]

26. For each subgraph J ⇢ [t],
we define the sequence of subgraph estimators as
ˆSJ,t =
Q
i2J
ˆSi,t
E[ ˆSJ,t] = SJ,t
We prove the sequence is a Martingale (Theorem 2)
Subgraph Estimation
[Ahmed et al, VLDB 2017]

27. Subgraph Counting
For any set J of subgraphs of G,
ˆNt(J ) =
P
J2J :J⇢Kt
ˆSJ,t
is an unbiased estimator of Nt(J ) = |Jt|
(Theorem 2)
[Ahmed et al, VLDB 2017]

28. § We provide a cost minimization approach
• inspired by IPPS sampling in i.i.d data [Cohen et al. 2005]
§ By minimizing the conditional variance of the increment
incurred by the arriving edge in
How the ranks ri,t should be distributed in order to minimize
the variance of the unbiased estimator of Nt(J )?
Nt(J )

29. § Post-stream Estimation
• Constructs a reference sample for retrospective queries
• after any number t of edge arrivals have taken place, we can
compute an unbiased estimate for the count of arbitrary subgraphs
§ In-stream Estimation
• we can take “snapshots” of estimates of specific sampled subgraphs
at arbitrary times during the stream
• Still Unbiased!
• Lightweight online/incremental update of unbiased estimates of
subgraph counts
• Same sampling procedure

30. Input
Graph Priority Sampling Framework
GPS(m)
Output
For each edge k
Edge stream
k1, k2, ..., k, ...
Sampled Edge stream ˆK
Stored State m = O(| ˆK|)
Compute edge priority
r(k) = w(k)/u(k)
Update the sample
Update unbiased estimates
of subgraph counts

31. In-stream Estimation
We define a snapshot as an edge subset J, with a family of
stopping times T such that T = {Tj : j 2 J}
We prove the sequence is a stopped Martingale (Theorem 4)
ˆST
J,t =
Q
j2J
ˆS
Tj
j,t =
Q
j2J
ˆSj,min{Tj ,t}
E[ ˆST
J,t] = SJ,t
[Ahmed et al, VLDB 2017]

32. Sample (S)
Overlapping
Triangles
Non-
Overlapping
Triangles
Multiple stopping
times for the
common edge

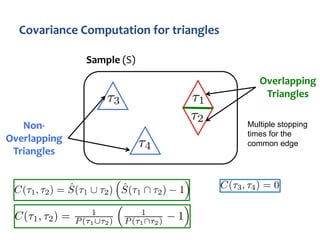
33. q Different weighting schemes lead to
different algorithms
- Uniform weights -> uniform sampling
q Ability to incorporate auxiliary variables
- Using the weight function
q Post-stream estimation
- construction of reference samples
for retrospective queries
q In-stream Estimation
- Maintains the desired query answer
(/variance) and update it accordingly
-> in a sketching fashion
For each edge k
Generate a random number
u(k) ⇠ Uni(0, 1]
Compute edge weight
w(k) = W(k, ˆK)
Compute edge priority
r(k) = w(k)/u(k)

34. § We use GPS for the estimation of
• Triangle counts
• Wedge counts
• Global clustering coefficient
• And their unbiased variance (Theorem 3 in the paper)
• Weight function
• Used a large set of graphs from a variety of domains (social, we,
tech, etc) - data is available on http://networkrepository.com/
— Up to 49B edges
W(k, ˆK) = 9 ⇤ ˆ4(k) + 1
where ˆ4(k) is the number of triangles
completed by edge k and whose edges in ˆK

35. - GPS accurately estimates various properties simultaneously
- Consistent performance across graphs from various domains
- A key advantage for GPS in-stream has smaller variance and tight confidence bounds

36. Results for triangle counts
Using massive real-world and synthetic graphs of up to 49B edges
GPS is shown to be accurate with <0.01 error
Sample size = 1M edges, in-stream estimation
95% confidence intervals

37. 10
4
10
5
0.6
0.7
0.8
0.9
1
1.1
1.2
1.3
1.4
soc−twitter−2010
Sample Size |K|
x/x
10
4
10
5
0.6
0.7
0.8
0.9
1
1.1
1.2
1.3
1.4
soc−twitter−2010
Sample Size |K|
x/x
Global Clustering Coeff
10
4
10
5
0.6
0.7
0.8
0.9
1
1.1
1.2
1.3
1.4
soc−twitter−2010
Sample Size |K|
x/x
10
4
10
5
0.6
0.7
0.8
0.9
1
1.1
1.2
1.3
1.4
soc−twitter−2010
Sample Size |K|
x/x
Triangle Count
10
4
10
5
0.9
0.92
0.94
0.96
0.98
1
1.02
1.04
1.06
1.08
1.1
soc−twitter−2010
Sample Size |K|
x/x
10
4
10
5
0.9
0.92
0.94
0.96
0.98
1
1.02
1.04
1.06
1.08
1.1
soc−twitter−2010
Sample Size |K|
x/x
Wedge Count
Actual
Estimated/Actual
Confidence Upper & Lower Bounds
Sample Size = 40K edges
Accurate estimates for large Twitter graph ~ 265M edges, and 17.2B triangles
95% confidence intervals

38. Global Clustering CoeffTriangle Count Wedge Count
Actual
Estimated/Actual
Confidence Upper & Lower Bounds
Sample Size = 40K edges
Accurate estimates for large social network Orkut ~ 120M edges, and 630M triangles
95% confidence intervals
10
4
10
5
10
6
0.9
0.92
0.94
0.96
0.98
1
1.02
1.04
1.06
1.08
1.1
soc−orkut
Sample Size |K|
x/x
10
4
10
5
10
6
0.9
0.92
0.94
0.96
0.98
1
1.02
1.04
1.06
1.08
1.1
soc−orkut
Sample Size |K|
x/x
10
4
10
5
10
6
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
soc−orkut
Sample Size |K|
x/x
10
4
10
5
10
6
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
soc−orkut
Sample Size |K|
x/x
10
4
10
5
10
6
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
soc−orkut
Sample Size |K|
x/x
10
4
10
5
10
6
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
soc−orkut
Sample Size |K|
x/x

39. 0 2 4 6 8 10 12
x 10
7
0.5
1
1.5
2
2.5
3
3.5
4
4.5
5
5.5
x 10
8
Stream Size at time t (|Kt|)
Trianglesattimet(xt)
soc−orkut
Actual
Estimate
Upper Bound
Lower Bound
0 2 4 6 8 10 12
x 10
7
0.5
1
1.5
2
2.5
3
3.5
4
4.5
5
5.5
x 10
8
Stream Size at time t (|Kt|)
Trianglesattimet(xt)
soc−orkut
0 2 4 6 8 10 12
x 10
7
0.005
0.01
0.015
0.02
0.025
0.03
0.035
0.04
Stream Size at time t (|Kt|)
ClusteringCoeff.attimet(xt)
soc−orkut
Actual
Estimate
Upper Bound
Lower Bound
0 2 4 6 8 10 12
x 10
7
0.005
0.01
0.015
0.02
0.025
0.03
0.035
0.04
Stream Size at time t (|Kt|)
ClusteringCoeff.attimet(xt)
soc−orkut
GPS in-stream estimates over time
Sample size = 80K edges
95% confidence intervals

40. 0.994 0.996 0.998 1 1.002 1.004 1.006
0.994
0.996
0.998
1
1.002
1.004
1.006
ca-hollywood-2009
com-amazon
higgs-social-network
soc-flickr
soc-youtube-snap
socfb-Indiana69
socfb-Penn94
socfb-Texas84
socfb-UF21
tech-as-skitter
web-BerkStan
web-google
GPS In-stream Estimation, sample size 100K edges
GPS accurately estimates both triangle and wedge counts
simultaneously with a single sample

42. We observe accurate results with no significant difference in error between
the ordering schemes

43. § We used three schemes for weighting edges during sampling
§ Goal: estimate triangle counts for Friendster social network
with sample size=1M (0.1% of the graph)
1. triangle-based weights (3% relative error)
2. wedge-based weights (25% relative error)
3. uniform weights for all incoming edges (43% relative error)
- this is equivalent to simple random sampling
The estimator variance was 3.8x higher using wedge-based weights, and
6.2x higher using uniform weights compared to triangle-based weights.

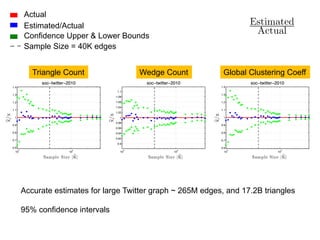
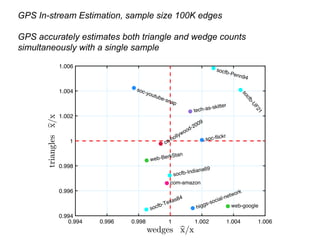
44. (1) Challenges for streaming graph analysis
(2) A framework for sampling/summarization of massive
streaming graphs
✓
✓
[Ahmed et al., VLDB 2017], [Ahmed et al., IJCAI 2018]

45. § Queries Beyond triangles
• Higher-order subgraphs
§ Streaming bipartite network projection
§ Approximate one-mode bipartite graph projection
§ To estimate similarity among one set of the nodes
§ Adaptive sampling
• Adaptive weights vs fixed weight
• Insertion/deletion streams – other dynamics
§ Batch computations, libraries …
To appear [Ahmed et al., IJCAI 2018]
To appear [Ahmed et al., IJCAI 2018]

46. § A sample is representative if graph properties of interest can be
estimated with a known degree of accuracy
§ Graph Priority Sampling (GPS) – unifying framework
- GPS is an efficient single-pass streaming framework
§ GPS is general and agnostic to the desired query
• Allows the dependence of the sampling process as a function of the stored
state and/or auxiliary variables
§ GPS is variance minimizing sampling approach
§ GPS has a relative estimation error < 1%

47. § On sampling from massive graph streams. VLDB 2017, [Ahmed et al.]
§ Sampling for Bipartite Network Projection. IJCAI 2018, [Ahmed et al.]
§ A space efficient streaming algorithm for triangle counting using the birthday paradox. KDD 2013, [Jha et. al]
§ Counting and Sampling Triangles from a Graph Stream. VLDB 2013. {Pavan et. al]
§ Efficient Graphlet Counting for Large Networks. ICDM 2015, [Ahmed et al.]
§ Graphlet Decomposition: Framework, Algorithms, and Applications. J. Know. & Info. 2016 [Ahmed et al.]
§ Estimation of Graphlet Counts in Massive Networks. IEEE TNNLS 2018 [Rossi-Zhou-Ahmed]
§ MASCOT: Memory-efficient and Accurate Sampling for Counting Local Triangles in Graph Streams. KDD 2015. [Lim et. al]
§ Network Motifs: Simple Building Blocks of Complex Networks. Science 2002, [Milo et al.]
§ Graph Sample and Hold: A Framework for Big Graph Analytics. KDD 2014 [Ahmed-Duffield-Neville-Kompella]
§ Role Discovery in Networks. IEEE TKDE 2015 [Rossi-Ahmed]
§ Efficient semi-streaming algorithms for local triangle counting in massive graphs. KDD 2008 [Becchetti et al.]
§ Random sampling with a reservoir. ACM Transactions on Mathematical Software (TOMS) 1985. [Vitter]

48. Thank you!
Questions?
nesreen.k.ahmed@intel.com
http://nesreenahmed.com