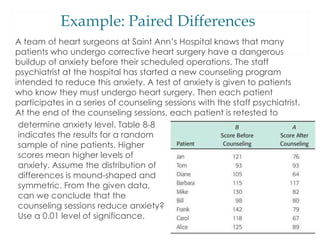
Many statistical tests use paired data samples to compare two population means. Paired data occurs naturally in "before and after" situations where the same item is measured before and after a treatment. When testing paired data, the proper procedure is to run a one-sample test on the differences between each pair of measurements. This allows researchers to determine if a treatment had a statistically significant effect based on the average difference between paired measurements.

1. 8.4 TESTS INVOLVING
PAIRED DIFFERENCES
(DEPENDENT SAMPLES)

2. Paired Data
• Many statistical applications use paired data
samples to draw conclusions about the difference
between two population means.
• Data pairs occur very naturally in “before and
after” situations, where the same object or item is
measured both before and after a treatment.
• Other situations: identical twins, a person’s left and right foot

3. Paired Data
• When a test involves comparing two populations for
which the data occur in pairs, the proper
procedure is to run a one-sample test on a single
variable consisting of the differences from the
paired data.
• Note: we did one-sample testing in 8.1 – 8.3

4. Components of the Paired Test
•

5. Components of the Paired Test
•

6. Components of the Paired Test
•

7. Components of the Paired Test
•

8. Calculating the P-Value
•

9. •

10. Example: Paired Differences
A team of heart surgeons at Saint Ann’s Hospital knows that many
patients who undergo corrective heart surgery have a dangerous
buildup of anxiety before their scheduled operations. The staff
psychiatrist at the hospital has started a new counseling program
intended to reduce this anxiety. A test of anxiety is given to patients
who know they must undergo heart surgery. Then each patient
participates in a series of counseling sessions with the staff psychiatrist.
At the end of the counseling sessions, each patient is retested to
determine anxiety level. Table 8-8
indicates the results for a random
sample of nine patients. Higher
scores mean higher levels of
anxiety. Assume the distribution of
differences is mound-shaped and
symmetric. From the given data,
can we conclude that the
counseling sessions reduce anxiety?
Use a 0.01 level of significance.

11. Example: Paired Differences
SOLUTION
•

12. Example: Paired Differences
SOLUTION
•
L2 L1
L3

13. Example: Paired Differences
SOLUTION
•

14. Example: Paired Differences
SOLUTION
•