1. สถิติเชิงพรรณนาและสถิติเชิงอนุมาน สัปดาห์ที่ 7-8 427-305 Statistics for Social Research อาจารย์มานพ จิตต์ภูษา อาจารย์อัลญาณ์ สมุห์เสนีโต

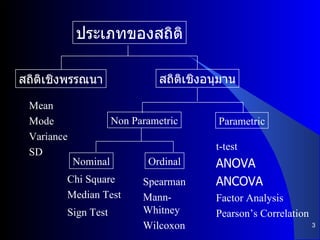
2. ความหมายของสถิติ ข้อมูลตัวเลข ( Numerical Data) เช่น สถิติปริมาณนิสิต สถิตจำนวนนิสิตที่มีผลการเรียนต่ำ สถิติปริมาณนิสิตที่ไม่จบการศึกษา วิชาสถิติ ( Statistics) สถิติพรรณนา ( Descriptive Statistics) สถิติอนุมาน ( Inference Statistics)

3. ประเภทของสถิติ สถิติเชิงพรรณนา สถิติเชิงอนุมาน Non Parametric Parametric Mean Mode Variance SD Chi Square Median Test Sign Test Spearman Mann-Whitney Wilcoxon t-test ANOVA ANCOVA Factor Analysis Pearson’s Correlation Nominal Ordinal

4. ประเภทของสถิติ สถิติพรรณนา ( Descriptive Statistics) คือ สถิติที่ใช้ในการอธิบาย หรือบรรยายลักษณะของข้อมูล เป็นการบรรยายลักษณะเฉพาะกลุ่มที่เก็บรวบรวมข้อมูลมา ไม่สามารถนำผลไปอ้างอิง หรือพยากรณ์ค่าของกลุ่มอื่น ๆ ได้ ตัวอย่าง จากการศึกษารายจ่ายรายเดือนของนิสิตมหาวิทยาลัยบูรพา พบว่า จากนิสิตที่สุ่มมาทั้งหมด 100 คน มีรายจ่ายรายเดือนเฉลี่ยคนละ 3,500 บาท สถิติอนุมาน ( Inference Statistics) คือ สถิติที่ได้มาจากข้อมูลของกลุ่มตัวอย่าง ( sample) แล้วนำไปอธิบายหรือสรุปผลลักษณะของประชากร ( population) ตัวอย่าง จากรายจ่ายโดยเฉลี่ยรายเดือนของนิสิต 3,500 บาท ดังกล่าวมาแล้ว และโดยอาศัยทฤษฎีความน่าจะเป็น ทำการประมาณรายจ่ายโดยเฉลี่ยรายเดือนของนิสิตทั้งหมดในมหาวิทยาลัยบูรพาได้เป็นระหว่าง 3,300 และ 3,700 บาท

5. สถิติเชิงพรรณนา , สถิติเชิงอนุมาน สถิติเชิงพรรณา (Descriptive Statistics) ใช้กับกลุ่มประชากร ได้แก่ Mean, Mode, Median, Variance, Standard Deviation เป็นต้น สถิติเชิงอนุมาน (Inference Statistics) เป็นสถิติเชิงทดสอบสมมุติฐาน ว่าสมมติฐานที่ตั้งไว้เป็นจริงหรือไม่ ได้แก่การประเมินค่าพารามิเตอร์ในประชากร (Estimation) และการทดสอบสมมุติฐาน (Hypothesis Testing) แบ่งออกเป็น Parametric และ Non parametric statistics

6. สถิติพรรณนา การนำเสนอข้อมูล ( Presentation) เช่น บทความ ตารางร้อยละ กราฟ หรือรูปภาพ การแจกแจงความถี่ ( Frequency) เช่น หาค่าร้อยละแบบทางเดียว และแบบหลายทาง การวัดแนวโน้มเข้าสู่ส่วนกลาง ( Central of Tendency) เช่น หาค่าตัวกลาง ( Mean) ค่าฐานนิยม ( Mode) หาตำแหน่งของข้อมูล เช่น มัธยฐาน ( Median) ควอไทล์ ( Quartiles) เดไซล์ ( Decile) เปอร์เซ็นไทล์ ( Percentiles) N- ไทล์ ( N-tiles) การวัดการกระจาย ( Dispersion) เช่น พิสัย ( Range) ส่วนเบี่ยงเบนควอไทล์ ( Quartile Deviation) ส่วนเบี่ยงเบนเฉลี่ย ( Mean or Average Deviation) ส่วนเบี่ยงเบนมาตรฐาน ( Standard Deviation) ค่าแปรปรวน ( Variance) สัมประสิทธิ์ของการกระจาย ( Coefficient of Variation) ความโค้งปกติ เช่น ความเบ้ ( Skewness) และความโด่ง ( Kurtosis)

7. สถิติเชิงพรรณนา : การวัดตำแหน่งหรือตำแหน่งกลาง เป็นการอธิบายลักษณะของข้อมูลว่า หน่วยศึกษา (subject หรือ observation) เกาะกลุ่มกันอยู่ตรงไหน การเปรียบเทียบค่าจากการวัดตำแหน่งหรือตำแหน่งกลางของข้อมูลสองชุดทำให้ทราบการเปลี่ยนแปลงเชิงตำแหน่งของข้อมูล การวัดตำแหน่งหรือตำแหน่งกลาง โดยทั่วไปมีหลายวิธี ได้แก่ การหาค่าเฉลี่ย (Mean) ค่ามัธยฐาน (Median) ฐานนิยม (Mode) ในร้อยส่วน (Percentile) และในสี่ส่วน (Quartile)

8. ค่าเฉลี่ย (Mean) คำนวณจากค่าของหน่วยศึกษาทุกหน่วยรวมกันหารด้วยจำนวนหน่วยที่ศึกษาทั้งหมด ค่าเฉลี่ยจะบอกว่าในภาพรวมหน่วยที่ศึกษามีค่ากลางของข้อมูลอยู่ที่ประมาณเท่าไหร่ ค่าเฉลี่ยของตัวอย่างและค่าเฉลี่ยของประชากร

9. ค่ามัธยฐาน ค่าที่อยู่ตรงกลางของชุดข้อมูลที่มีการเรียงลำดับแล้วหรือกล่าวได้ว่าค่ามัธยฐานคือ ค่าของหน่วยที่ศึกษาที่อยู่ในลำดับที่ (n+1)/2 เมื่อ n คือ จำนวนหน่วยที่ศึกษาทั้งหมดในข้อมูลชุดนั้น ค่าฐานนิยม - ค่าของหน่วยที่ศึกษาที่มีความถี่มากที่สุด

10. การวัดการกระจาย พิสัย หมายถึง ช่วงห่างระหว่างค่าสูงสุดกับค่าต่ำสุดของข้อมูลชุดนั้น ค่าเบี่ยงเบนมาตรฐาน (standard deviation, S.D.) หมายถึงการกระจายของข้อมูลที่มองในรูปผลรวมของระยะห่างของ ค่าสังเกตแต่ละค่า จากค่าเฉลี่ย คำนวณจากค่าผลรวมค่าเบี่ยงเบนขอ ค่าสังเกตแต่ละค่าจากค่าเฉลี่ยยกกำลังสองหารด้วยจำนวนค่าสังเกต ทั้งหมด

11. การบ้านสัปดาห์ที่ 7 1. จงหาค่าเฉลี่ย มัธยฐาน และฐานนิยมจากข้อมูลต่อไปนี้ 1 1 2 4 5 7 8 9 12 12 13 130 2. ในการขายแพะ 500 ตัว ซึ่งมีน้ำหนักโดยเฉลี่ย 6.3 กิโลกรัมต่อตัว ก . หาน้ำหนักรวมแพะทั้ง 500 ตัวนี้ ข . ถ้าราคาของแพะเท่ากับกิโลกรัมละ 100 บาท และมีค่าการจัดการอีกตัวละ 20 บาท จงหาราคารวมของแพะทั้งหมด ( รวมค่าจัดการ ) และหาราคาเฉลี่ยต่อตัวของแพะ ( รวมค่าจัดการ )

12. สัปดาห์ที่ 8: สถิติเชิงอนุมาน

13. สถิติอนุมาน แบบมีพารามิเตอร์ เป็นการนำค่าที่ได้จากตัวอย่าง ซึ่งจะเรียกว่า ค่าสถิติ ( statistics) ไปอธิบายคุณลักษณะประชากร ซึ่งจะเรียกว่า ค่าพารามิเตอร์ ( parameter) แบบไม่มีพารามิเตอร์ เป็นการอนุมานข้อมูลจากตัวอย่างไปอธิบายลักษณะของประชากรในกรณีที่ไม่ทราบค่าของข้อมูลจากประชากรที่สนใจ ไม่ทราบการแจกแจงแบบใด ค่าของข้อมูลที่ได้มาจากตัวอย่างอยู่ในระดับนามมาตรา (Nominal Scale) หรืออันดับมาตรา (Ordinal Scale) และกลุ่มตัวอย่างที่เลือกมามีขนาดเล็ก หรือจำนวนน้อย

14. การประมวลผลข้อมูลด้วยสถิติเบื้องต้น การพรรณนาและวิเคราะห์ข้อมูลเป็นจำนวนและร้อยละ Frequencies, Crosstabs การพรรณนาและวิเคราะห์ข้อมูลเป็นค่าเฉลี่ย Descriptive, Mean, T-Test การวิเคราะห์ข้อมูลเพื่อแสดงความสัมพันธ์ Crosstabs, Correlation, Regression

15. การวิเคราะห์ข้อมูล ในการวิเคราะห์ข้อมูลปัจจุบันนิยมใช้สถิติที่เป็นโปรแกรมคอมพิวเตอร์สำเร็จรูปเพื่อการวิจัย สถิติอาจแบ่งเป็น 2 ประเภท 1. สถิติพรรณนา (Descriptive statistics) 2. สถิติวิเคราะห์ (Analytical statistics) คือสถิติที่นำมาใช้เพื่อพิสูจน์หรือทดสอบสมมุติฐาน และยืนยันข้อค้นพบ ( เกี่ยวกับความแตกต่างหรือความสัมพันธ์ ระหว่างตัวแปรอิสระกับตัวแปรตาม )

16. การวิเคราะห์ข้อมูลและการแปลความหมายข้อมูล เมื่อเก็บรวบรวมข้อมูลมาแล้วนำมาทำการวิเคราะห็ การวิเคราะห์ข้อมูลสามารถทำได้หลายระดับ เช่น การวิเคราะห์ข้อมูลเบื้องต้น ได้แก่ จำนวน การแจกแจง ความถี่ การหาร้อยละ การหาค่ากลางหรือค่าเฉลี่ย การหาสัดส่วน ซึ่งนิยมใช้ในวิจัยเชิงคุณภาพ การวิเคราะห์ข้อมูลชั้นสูง ได้แก่ การทดสอบสมมุติฐานทางสถิติ หาความแตกต่าง หาความสัมพันธ์ เป็นต้น เช่น t-test, ANOVA, Chi-Square, Correlation, Regression เป็นสถิติที่ใช้ในการวิจัยเชิงปริมาณ

17. ขั้นตอนการเลือกใช้สถิติ ต้อง เลือก ตัวแปรอิสระ และตัวแปรตามให้ได้และถูกต้องก่อน การจะใช้ตัวสถิติอะไรนั้น ต้องดูว่าสถิติแต่ละตัวนั้นมีข้อกำหนดในการใช้ว่า ตัวแปรอิสระต้องวัดด้วยสเกลอะไร ตัวแปรต้องวัดด้วยสเกลอะไร ( และมีข้อกำหนดอื่นหรือไม่ ) ต้องรู้ว่าตัวสถิตินั้นใช้ทดสอบอะไร เช่น ทดสอบความสัมพันธ์ระหว่าง 2 ตัวแปร หาขนาดความสัมพันธ์ระหว่าง 2 ตัวแปร ทดสอบความแตกต่างค่าเฉลี่ย หารูปแบบความสัมพันธ์หลายตัวแปร เป็นต้น

18. ประเภทของสถิติ Parametric Non-Parametric RATIO INTERVAL ORDINAL NOMINAL Geometric Mean Coefficient of Variation Median, Percentile Spearman Kendall, Kendall W Mode, Frequency Contingency Coefficient

19. Parametric Statistics กลุ่มประชากรที่มีการแจกแจงแบบโค้งปกติ ข้อมูลทั้งหมดเรียกว่า Population ค่าที่คำนวณได้เรียก Parameter แต่ถ้าเก็บมาเพียงบางส่วนจากประชากรจะเรียก Sample ค่าที่ได้เรียกว่าค่าสถิติ (Statistics) มี ระดับการวัด แบบ Ratio หรือ Interval scale เช่น t-test, ANOVA, Correlation, Multiple Regression เป็นต้น

20. Non Parametric Statistics คือสถิติที่ใช้กับกลุ่มประชากรที่ไม่เข้าเงื่อนไขของ Parametric มี ระดับ การวัดแบบ Ordinal และ Nominal วิเคราะห์โดยการ ใช้วิธี Chi Square, Log Rank Test, Mann Whitney, Wilcoxon เป็นต้น

21. Alpha and Beta errors THE TRUTH CONCLUSION drawn from analysis A = B A = B Correct  Error  Error Correct Accept H 0 H 0 : A = B Accept H 1 H 1 : A = B