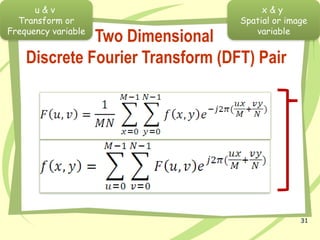
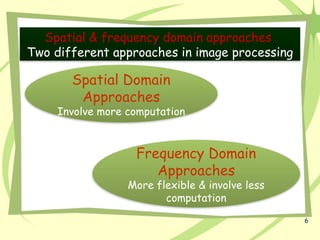
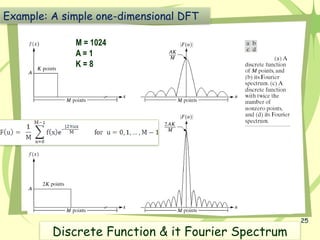
The document discusses image enhancement techniques, categorizing them into spatial and frequency domain methods. Filtering is emphasized as a crucial technique for improving image quality by manipulating pixel operations, and the significance of Fourier transforms in analyzing and processing both images and sound is explained. It details the mathematical foundations of Fourier series and transforms, showing how periodic functions can be decomposed into sinusoidal components, which can then be manipulated for various applications in image processing.

1. 1
IMAGE ENHANCEMENT
IN
FREQUENCY DOMAIN

2. 2
Image Enhancement
Purposes: To make an image better appealing
and easier to deal with than the original image
Three categories:
1. Spatial domain methods:
operate on the images itself,
Point processing, e.g., image averaging; logic operation;
contrast stretching ...
Mask processing, e.g., filtering or mask operation, (blurring,
median

3. 3
2. Frequency domain methods:
work on the Fourier transformed output
of the image, examples: from the
convolution theory
g(x,y) = f(x,y) ⊗ h(x,y)
=> G(u,v) = F(u,v) • H(u,v)
=> certain properties of F(u,v) can be
emphasized into G(u,v)
=> spatial domain g(x,y) = F-1
{G(u,v)}
3. Combination of the above two categories

4. 4
Recap
Filtering
Filtering is a technique for modifying or enhancing
an image. For example, you can filter an image to
emphasize certain features or remove other
features.
In principle, filtering is the term used for any
operation that is applied to pixels in an image. This
also includes smoothing, edge enhancement and
resolution recovery. Generally, the aim of filtering
is to allow improved extraction of relevant
information .

5. 5
So far we processed the image ‘directly’, i.e. the
transformation was a function of the image
itself.
We called this the SPATIAL domain.
So what’s the FREQUENCY domain ?

6. 6
Spatial & frequency domain approaches
Two different approaches in image processing
Spatial Domain
Approaches
Involve more computation
Frequency Domain
Approaches
More flexible & involve less
computation

7. 7
Let’s first forget about images, and look at SOUND.
SOUND: 1 dimensional function of changing (air-
pressure in time)
Pressure
Time t
If the function is periodic, we perceive it as sound
with a certain frequency (else it’s noise). The
frequency defines the pitch. The amplitude of the
curve defines the volume.

8. 8
The SHAPE of the curve defines the
sound character
Flute String
Brass

9. 9
Listening to an orchestra, you can distinguish
between different instruments, although the
sound is a SINGLE FUNCTION !
Flute
String
Brass

10. 10
If the sound produced by an
orchestra is the sum of different
instruments, could it be possible that
there are BASIC SOUNDS, that can
be combined to produce every single
sound ?

11. 11
The answer
(Charles Fourier, 1822):
Any function that periodically
repeats itself can be expressed as
the sum of sines/cosines of
different frequencies, each
multiplied by a different coefficient

12. Jean Baptiste Joseph Fourier (1768-1830)
• Had crazy idea (1807):
• Any periodic
function can be rewritten
as a weighted sum of Sines
and Cosines of different
frequencies.
• Don’t believe it?
– Neither did Lagrange,
Laplace, Poisson and
other big wigs
– Not translated into
English until 1878!
• But it’s true!
– called Fourier Series
– Possibly the greatest
tool
used in Engineering
12

13. 13
Periodic Signals
A continuous-time signal x(t) is periodic if:
x(t + T) = x(t)
Fundamental period
T0, of x(t) is smallest T satisfying above equation.
Fundamental frequency: f0 = 1/T0
Fundamental angular frequency:
ω0 = 2π/T0 = 2πf0

14. 14
y(x) = A sin(fx + p)
Any mathematical function that periodically repeats itself
can be expressed as a sum of sines &/or cosines with
different amplitudes A, frequencies f, and phases p.
Fourier Series
It does not matter how complicated the
function is – as long as it is periodic (&
meets certain mathematical conditions), it
can be represented by such a sum.

15. 15
Fourier Transform
Even functions that are not periodic
(but whose area under the curve is
finite) can be expressed as the integral
of sines &/or cosines multiplied by a
weighting function.

16. 16
Images are functions of
finite duration
Hence we
will be
dealing with
Fourier
Transform
tool

17. 17
Fourier Transform
&
The frequency Domain

18. 18
The One-Dimensional
Discrete Fourier Transform (DFT)
& its Inverse
The Fourier transform of a discrete
function of one variable, f(x), x = 0, 1, …,
M-1, is given by the following equation
where

19. 19
Conversely, given F(u), f(x) can be
obtained by means of the inverse Fourier
transform, i.e. we can obtain the original
function back using the inverse DFT

20. 20
To compute F(u):
1.Substitute u = 0 in the exponential term &
then sum for all values of x.
2.Next substitute u = 1 in the exponential &
repeat the summation over all values of x.
3.Repeat this process for all M values of u
in order to obtain the complete Fourier
transform.

21. 21
Each term of the Fourier transform is
composed of the sum of all values of the
function f(x)
The domain (values of u) over which
the values of F(u) range is called the
Frequency domain
because u determines the frequency
components of the transform

22. 22
Each of the M terms of F(u) are known
as
Frequency Component
of the transform

23. 23
Fourier Transform –
A “mathematical prism”

24. A prism which splits the
white light into different
colours (components with a
different wavelength /
frequency).
The prism acts like a
Fourier transform operator.
The Fourier transform is a mathematical procedure which
decomposes a signal into its sinusoid components with different
frequencies. Inverse procedure - the Inverse Fourier transform - can
be used to recombine the components into the composed signal. One
can manipulate the frequency components in the frequency space as
needed for different purposes.
Jean Baptiste Joseph Fourier (1768-1830) - the concept of the
transform first suggested in 1810 in the paper on heat conduction
24

25. 25
Example: A simple one-dimensional DFT
Discrete Function & it Fourier Spectrum
M = 1024
A = 1
K = 8

26. 26
The function f(x) for x = 0, 1, …, M-1
represents M samples
These samples are not necessarily always
taken at integer values of x. They are taken at
equally spaced, but otherwise arbitrary points.
x0 represents the I point in the sequence. The
I value of the sampled function is then f(x0).
The next sample has been taken a fixed
interval ∆x units away to give f(x0 + ∆x)

27. 27
The kth
sample gives us f(x0 + k x)
∆
The final sample is ?
f(x0 + [M-1] x)
∆

28. 28
Variable u has similar interpretation
But …
The sequence always starts at true zero
frequency. Thus, the sequence for the values
of u is 0, ∆u, 2∆u, …, [M-1]∆u
Inverse relationship exits between a
function & its transform. Hence

29. 29
The Two-Dimensional
Discrete Fourier Transform (DFT)
& its Inverse
The discrete Fourier transform of a
function (image) f(x, y) of size M x N is
given by following equation

30. 30
Similarly, given F(u, v), we can obtain
f(x, y) via inverse Fourier transform

31. 31
Two Dimensional
Discrete Fourier Transform (DFT) Pair
u & v
Transform or
Frequency variable
x & y
Spatial or image
variable

32. 32
A common
practice …
Multiply the i/p image function by (-1)x + y
prior to computing the Fourier transform
This shifts the origin of F(u, v) to frequency
coordinates (M/2, N/2),which is the centre of the
M x N area occupied by the 2-DFT

33. 33
The value of transform at (u, v) = (0, 0)
Which is the average of f(x, y)
f(x, y) is an image
The value of the Fourier transform at origin is
equal to the average gray-level of the image