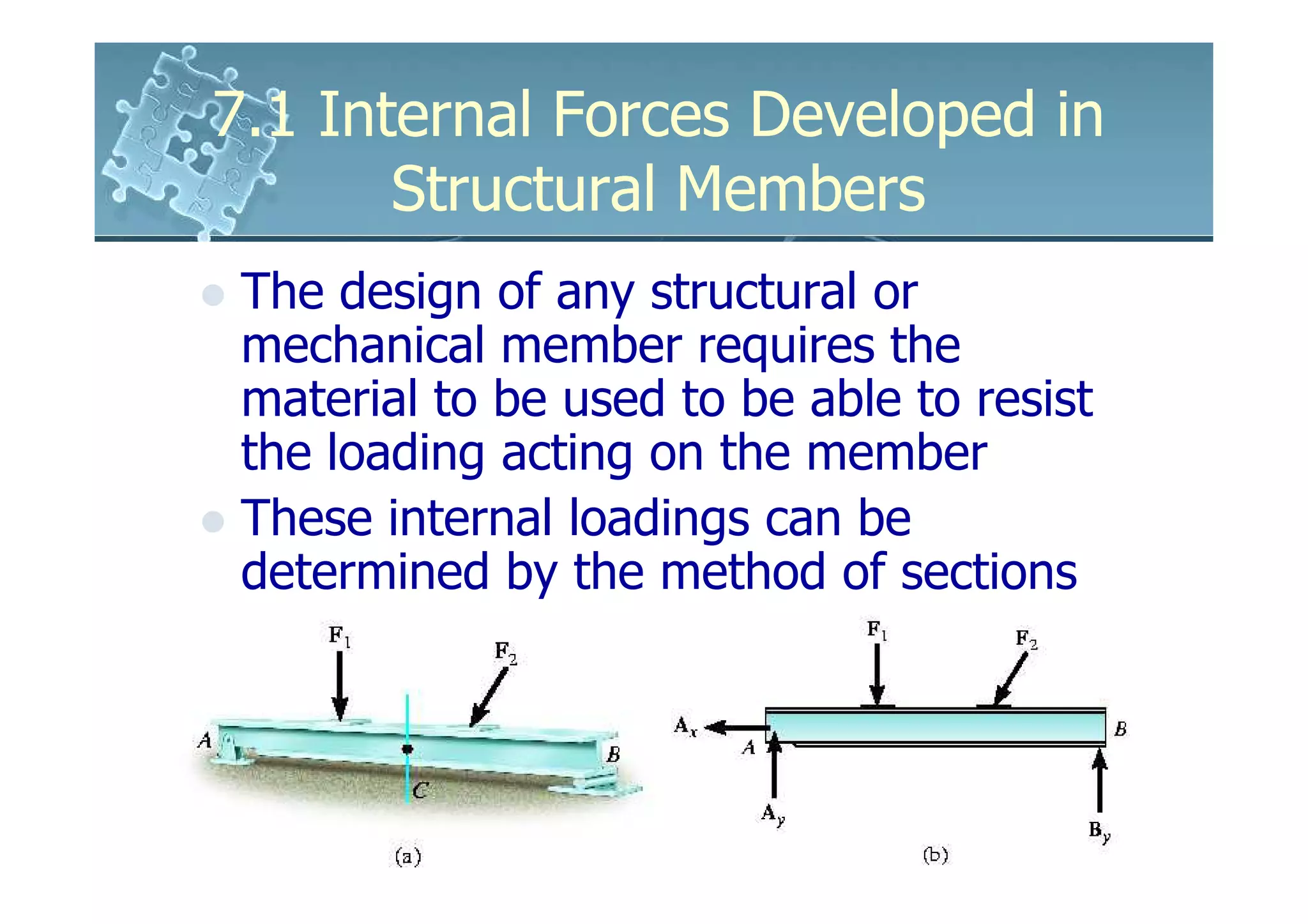
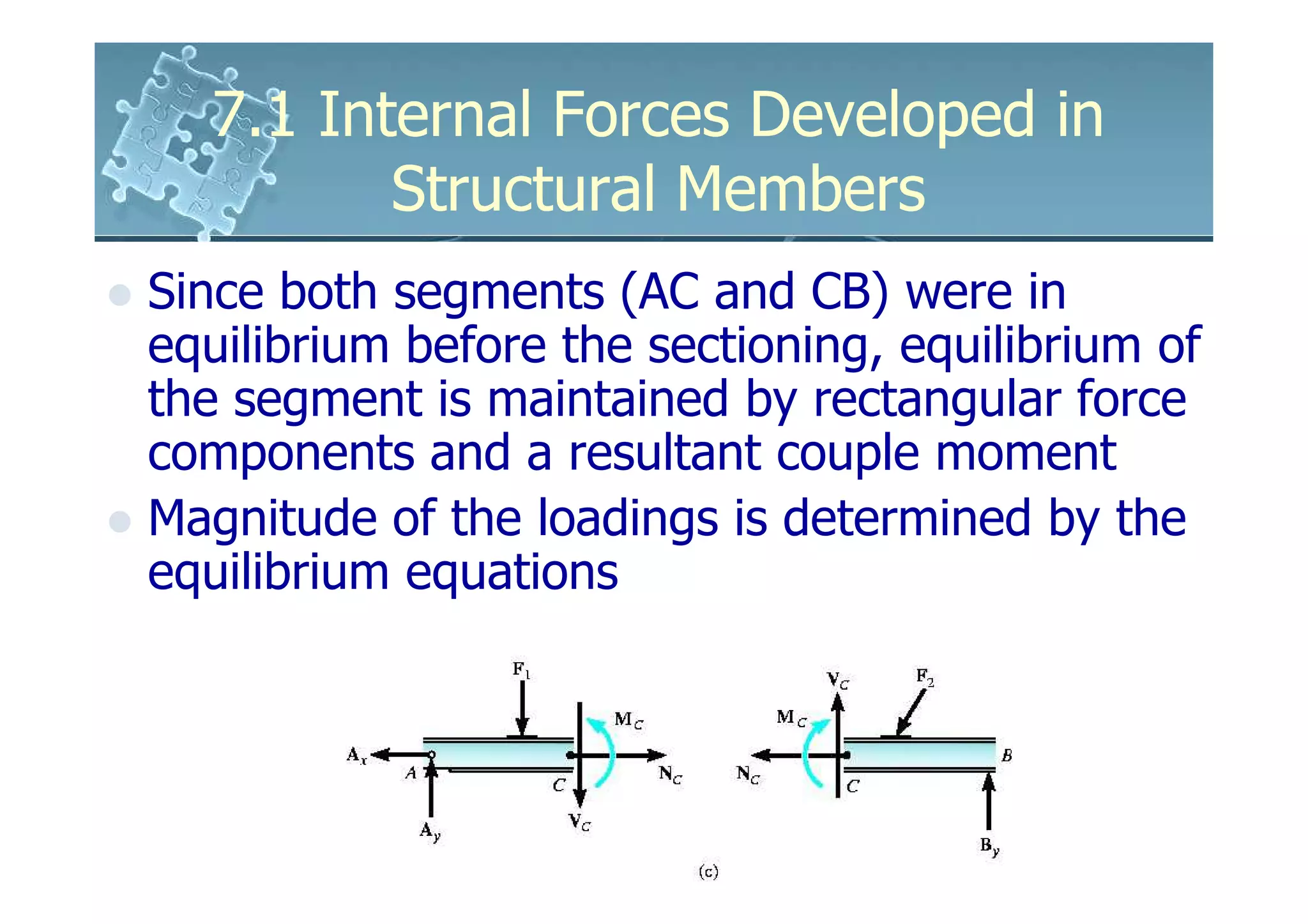
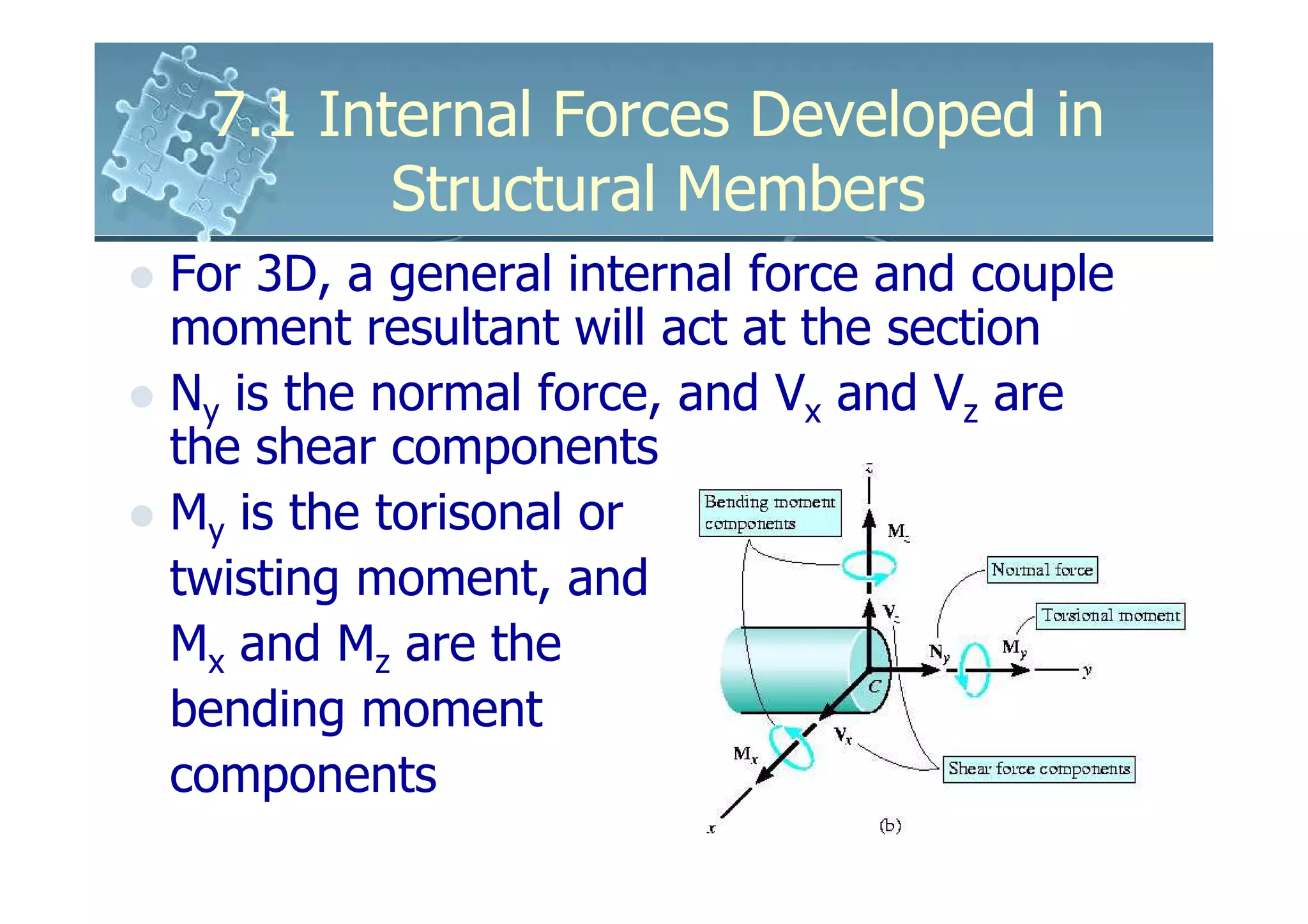
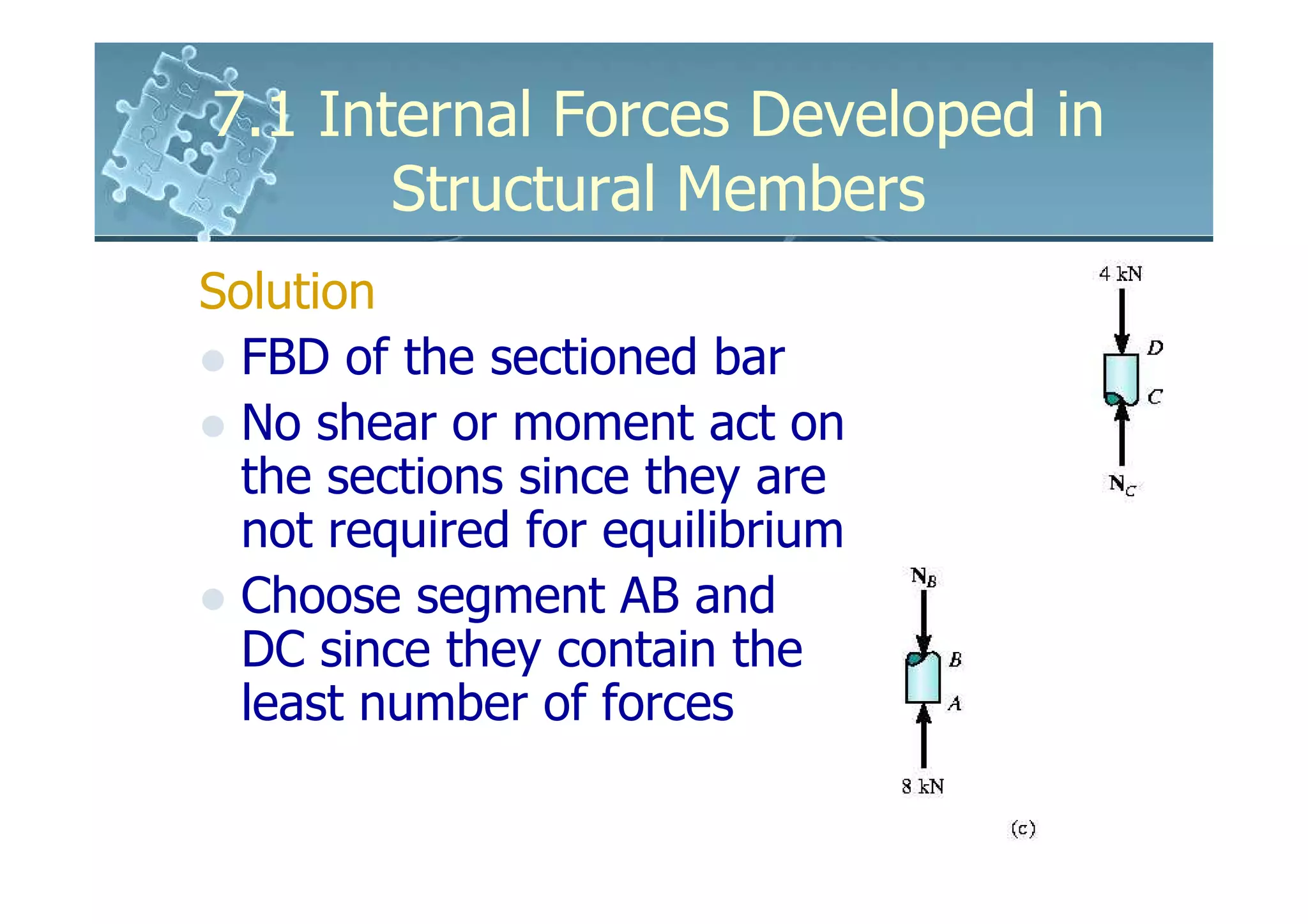
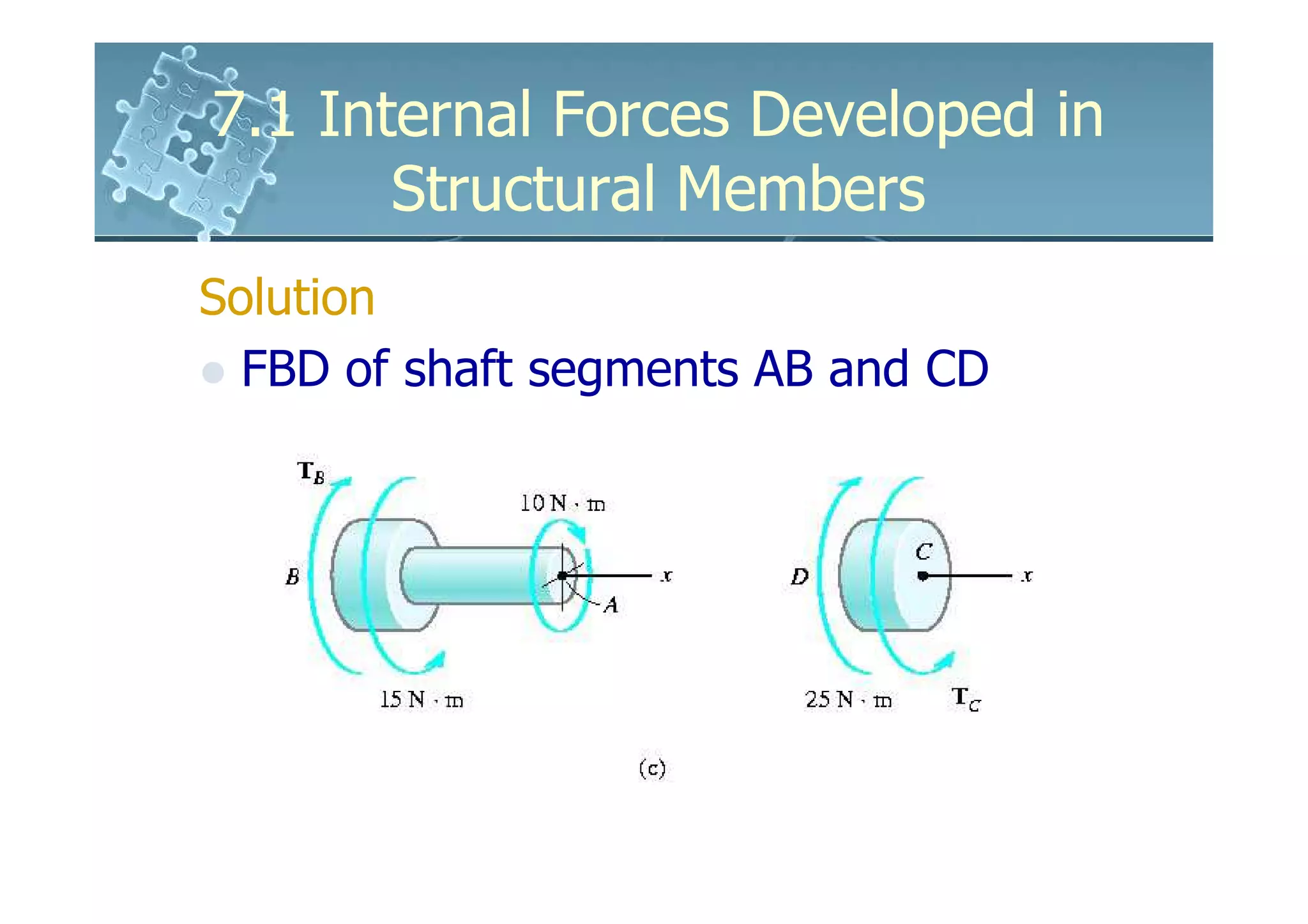
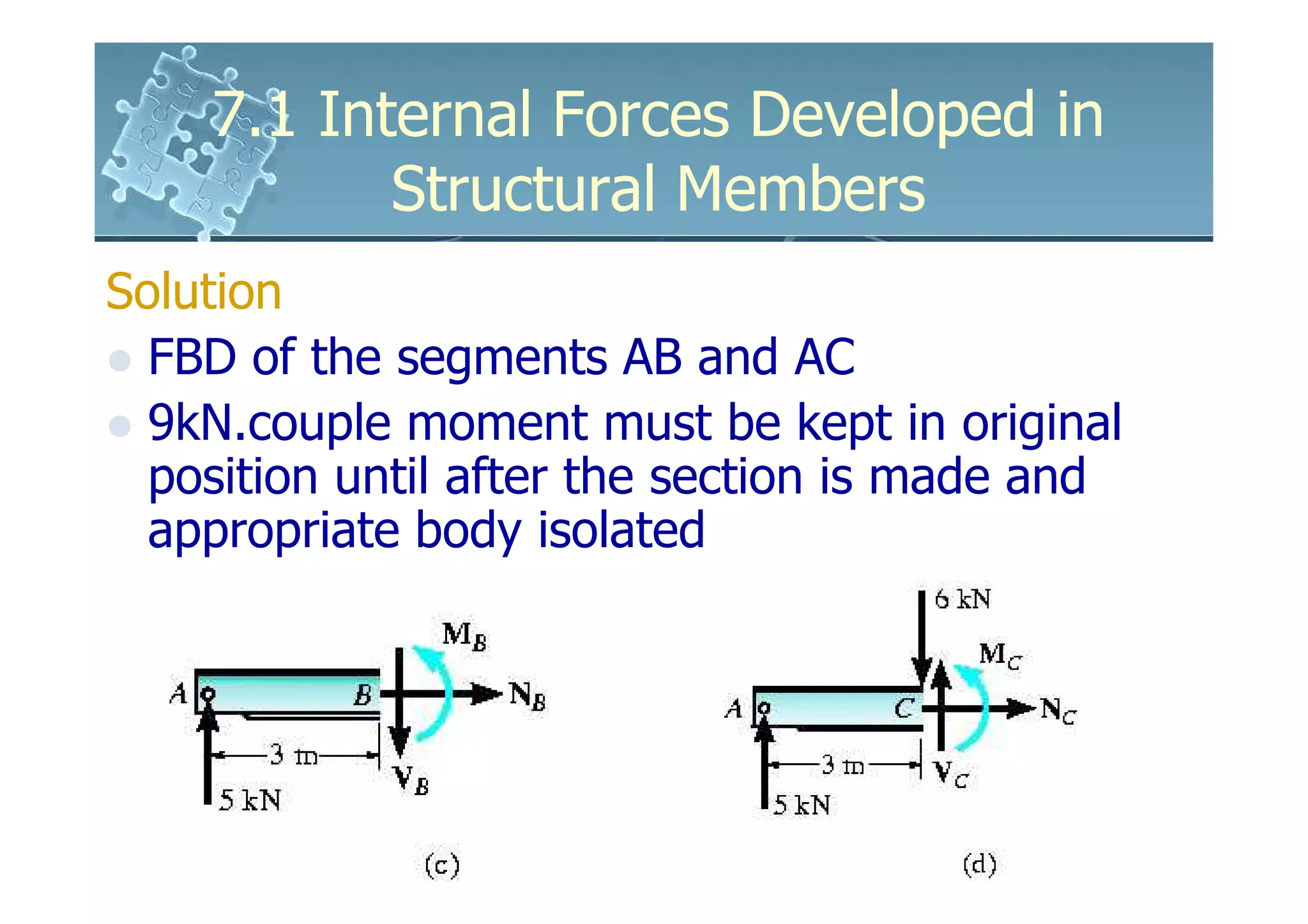
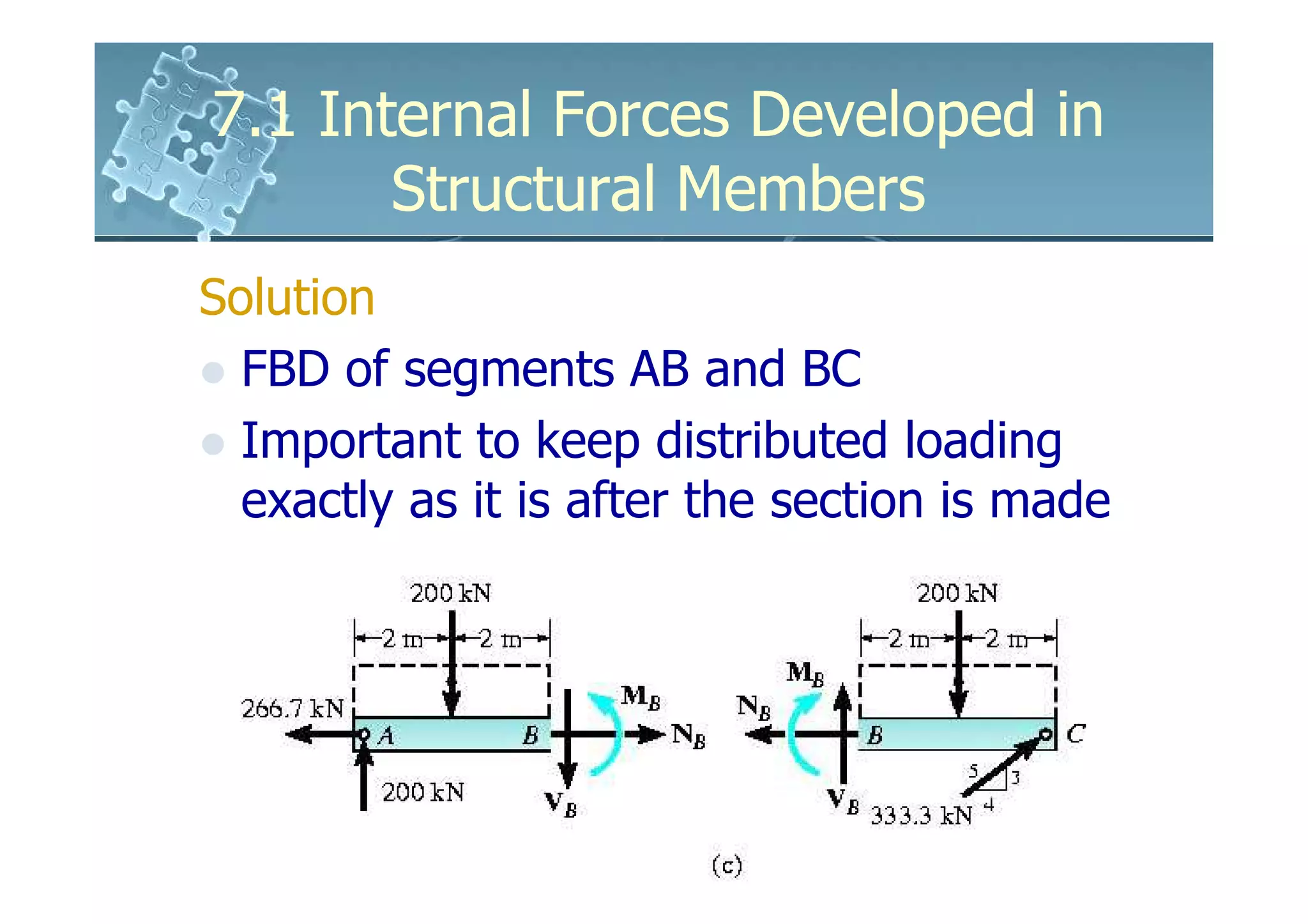
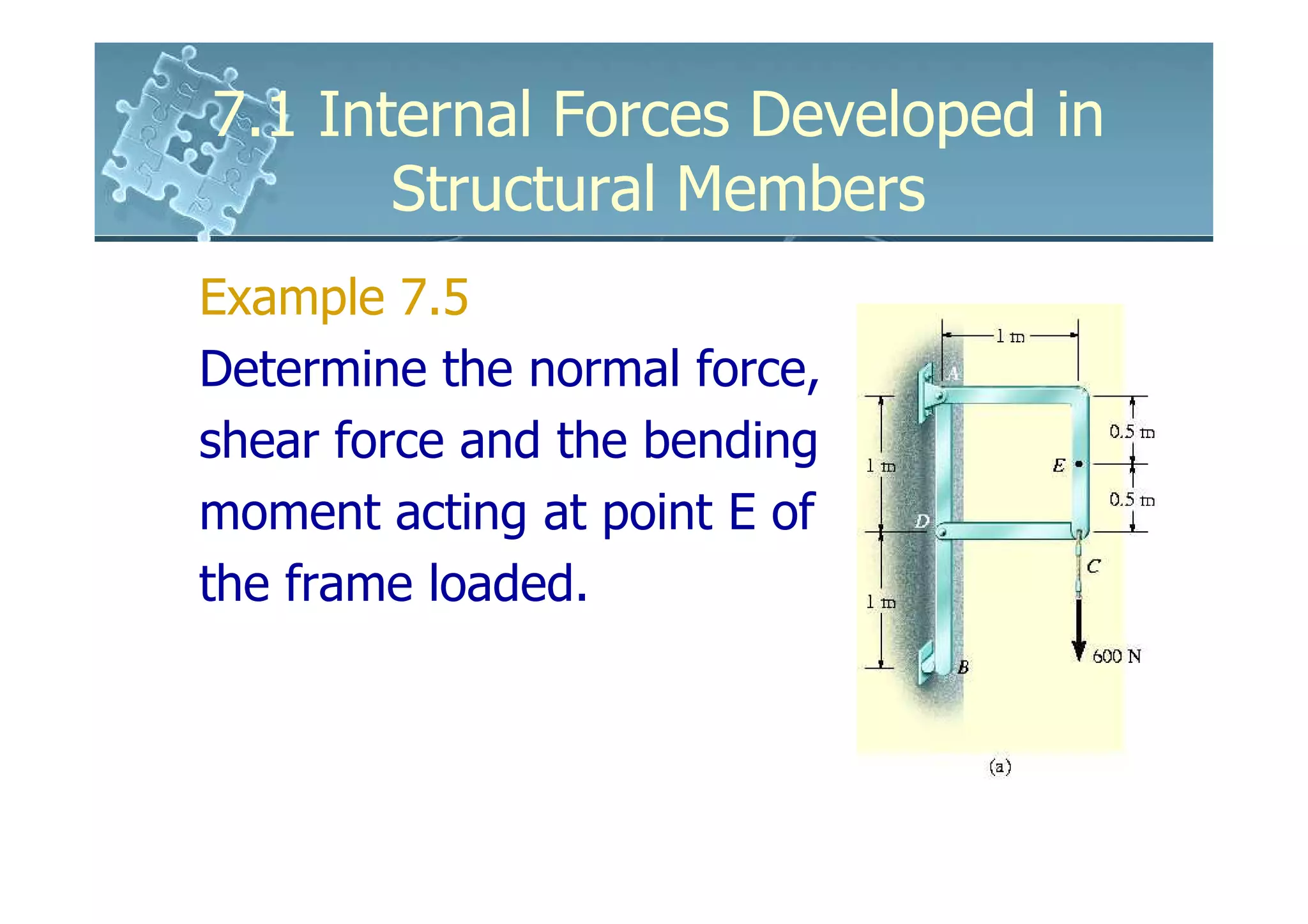
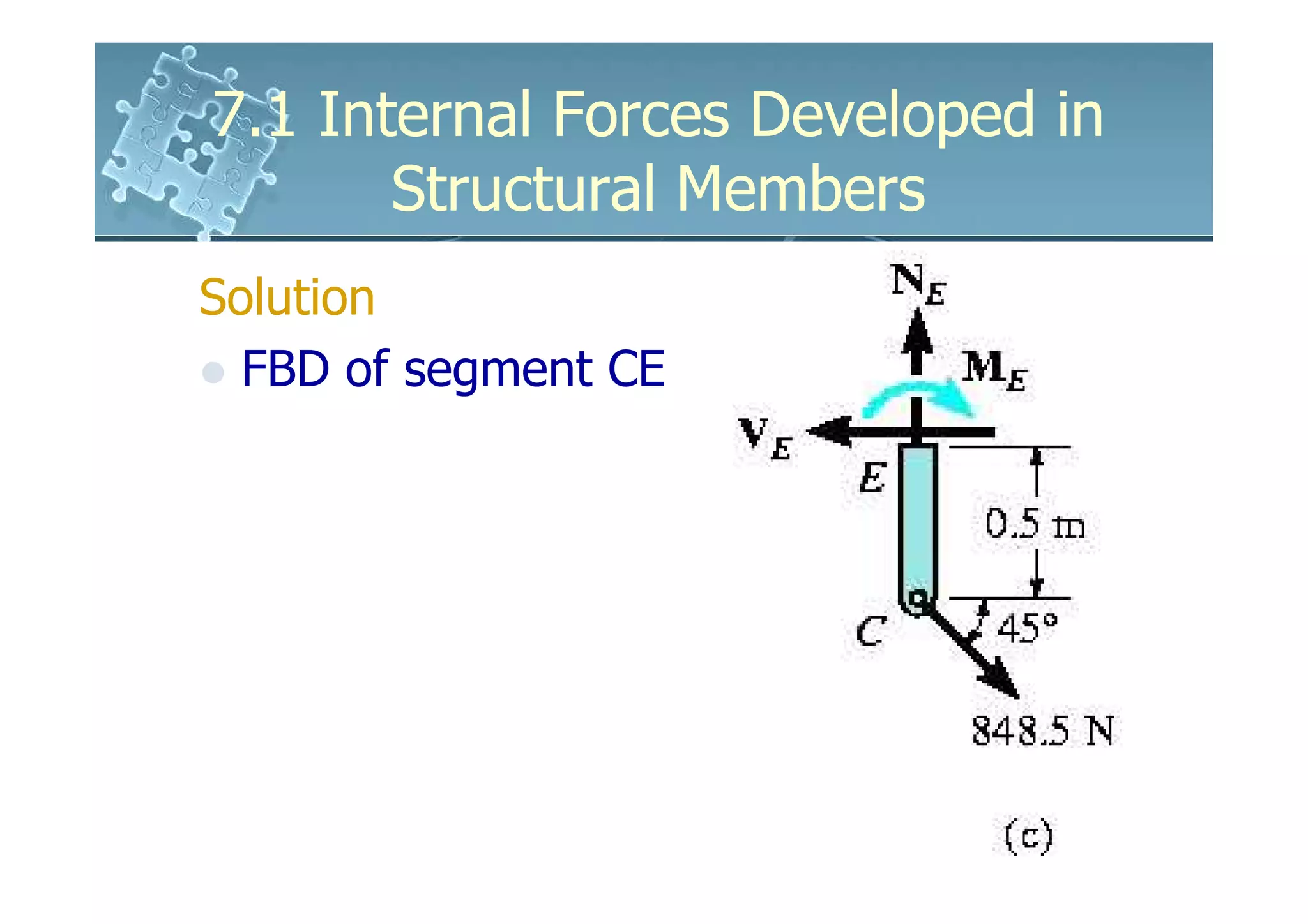
This document discusses how to determine the internal forces in structural members using the method of sections. It explains that an imaginary cut is made through the member to separate it into segments. The internal forces acting on the cut section become external forces on the free body diagrams of each segment. Equilibrium equations are then used to calculate the normal force, shear force, bending moment, and torsion at the cut section. Several examples are provided to demonstrate how to set up and solve for the internal forces using this method.

1. 7.1 Internal Forces Developed in
Structural Members
The design of any structural or
mechanical member requires the
material to be used to be able to resist
the loading acting on the member
These internal loadings can be
determined by the method of sections

2. 7.1 Internal Forces Developed in
Structural Members
Consider the “simply supported” beam
To determine the internal loadings acting on the cross
section at C, an imaginary section is passed through
the beam, cutting it into two
By doing so, the internal loadings become external on
the FBD

3. 7.1 Internal Forces Developed in
Structural Members
Since both segments (AC and CB) were in
equilibrium before the sectioning, equilibrium of
the segment is maintained by rectangular force
components and a resultant couple moment
Magnitude of the loadings is determined by the
equilibrium equations

4. 7.1 Internal Forces Developed in
Structural Members
Force component N, acting normal to the
beam at the cut session and V, acting t
angent to the session are known as normal
or axial force
and the shear force
Couple moment M is
referred as the bending
moment

5. 7.1 Internal Forces Developed in
Structural Members
For 3D, a general internal force and couple
moment resultant will act at the section
Ny is the normal force, and Vx and Vz are
the shear components
My is the torisonal or
twisting moment, and
Mx and Mz are the
bending moment
components

6. 7.1 Internal Forces Developed in
Structural Members
For most applications, these resultant
loadings will act at the geometric
center or centroid (C) of the section’s
cross sectional area
Although the magnitude of each
loading differs at different points along
the axis of the member, the method of
section can be used to determine the
values

7. 7.1 Internal Forces Developed in
Structural Members
Free Body Diagrams
Since frames and machines are composed of
multi-force members, each of these members will
generally be subjected to internal shear, normal
and bending loadings
Consider the frame with the blue
section passed through to
determine the internal loadings
at points H, G and F

8. 7.1 Internal Forces Developed in
Structural Members
Free Body Diagrams
FBD of the sectioned frame
At each sectioned member, there is an unknown
normal force, shear force and bending moment
3 equilibrium equations cannot be used
to find 9 unknowns, thus dismember
the frame and determine
reactions at each connection

9. 7.1 Internal Forces Developed in
Structural Members
Free Body Diagrams
Once done, each member may be sectioned at its
appropriate point and apply the 3 equilibrium
equations to determine the unknowns
Example
FBD of segment DG can be used to determine
the internal loadings at G
provided the reactions of
the pins are known

10. 7.1 Internal Forces Developed in
Structural Members
Procedure for Analysis
Support Reactions
Before the member is cut or sectioned,
determine the member’s support reactions
Equilibrium equations are used to solve for
internal loadings during sectioning of the
members
If the member is part of a frame or machine, the
reactions at its connections are determined by
the methods used in 6.6

11. 7.1 Internal Forces Developed in
Structural Members
Procedure for Analysis
Free-Body Diagrams
Keep all distributed loadings, couple
moments and forces acting on the member
in their exact locations, then pass an
imaginary section through the member,
perpendicular to its axis at the point the
internal loading is to be determined
After the session is made, draw the FBD of
the segment having the least loads

12. 7.1 Internal Forces Developed in
Structural Members
Procedure for Analysis
Free-Body Diagrams
Indicate the z, y, z components of the force and
couple moments and the resultant couple
moments on the FBD
If the member is subjected to a coplanar system
of forces, only N, V and M act at the section
Determine the sense by inspection; if not,
assume the sense of the unknown loadings

13. 7.1 Internal Forces Developed in
Structural Members
Procedure for Analysis
Equations of Equilibrium
Moments should be summed at the section about
the axes passing through the centroid or
geometric center of the member’s cross-sectional
area in order to eliminate the unknown normal
and shear forces and thereby, obtain direct
solutions for the moment components
If the solution yields a negative result, the sense
is opposite that assume of the unknown loadings

14. 7.1 Internal Forces Developed in
Structural Members
The link on the backhoe is a
two force member
It is subjected to both
bending and axial load at its
center
By making the member
straight, only an axial force
acts within the member

15. 7.1 Internal Forces Developed in
Structural Members
Example 7.1
The bar is fixed at its end and is
loaded. Determine the internal normal
force at points B and C.

16. 7.1 Internal Forces Developed in
Structural Members
Solution
Support Reactions
FBD of the entire bar
By inspection, only normal force Ay
acts at the fixed support
Ax = 0 and Az = 0
+↑∑ Fy = 0; 8kN – NB = 0
NB = 8kN

17. 7.1 Internal Forces Developed in
Structural Members
Solution
FBD of the sectioned bar
No shear or moment act on
the sections since they are
not required for equilibrium
Choose segment AB and
DC since they contain the
least number of forces

18. 7.1 Internal Forces Developed in
Structural Members
Solution
Segment AB
+↑∑ Fy = 0; 8kN – NB = 0
NB = 8kN
Segment DC
+↑∑ Fy = 0; NC – 4kN= 0
NC = 4kN

19. 7.1 Internal Forces Developed in
Structural Members
Example 7.2
The circular shaft is subjected to three
concentrated torques. Determine the internal
torques at points B and C.

20. 7.1 Internal Forces Developed in
Structural Members
Solution
Support Reactions
Shaft subjected to only collinear torques
∑ Mx = 0;
-10N.m + 15N.m + 20N.m –TD = 0
TD = 25N.m

21. 7.1 Internal Forces Developed in
Structural Members
Solution
FBD of shaft segments AB and CD

22. 7.1 Internal Forces Developed in
Structural Members
Solution
Segment AB
∑ Mx = 0; -10N.m + 15N.m – TB =
0
TB = 5N.m
Segment CD
∑ Mx = 0; TC – 25N.m= 0
TC = 25N.m

23. 7.1 Internal Forces Developed in
Structural Members
Example 7.3
The beam supports the loading. Determine
the internal normal force, shear force and bending
moment acting to the left, point B and just to the
right, point C of the 6kN force.

24. 7.1 Internal Forces Developed in
Structural Members
Solution
Support Reactions
9kN.m is a free vector and can be place
anywhere in the FBD
+↑∑ Fy = 0; 9kN.m + (6kN)(6m) - Ay(9m) = 0
Ay = 5kN

25. 7.1 Internal Forces Developed in
Structural Members
Solution
FBD of the segments AB and AC
9kN.couple moment must be kept in original
position until after the section is made and
appropriate body isolated

26. 7.1 Internal Forces Developed in
Structural Members
Solution
Segment AB
+→∑ Fx = 0; NB = 0
+↑∑ Fy = 0; 5kN – VB = 0
VB = 5kN
∑ MB = 0; -(5kN)(3m) + MB = 0
MB = 15kN.m
Segment AC
+→∑ Fx = 0; NC = 0
+↑∑ Fy = 0; 5kN - 6kN + VC = 0
VC = 1kN
∑ MC = 0; -(5kN)(3m) + MC = 0
MC = 15kN.m

27. 7.1 Internal Forces Developed in
Structural Members
Example 7.4
Determine the internal force, shear force and
the bending moment acting at point B of the
two-member frame.

28. 7.1 Internal Forces Developed in
Structural Members
Solution
Support Reactions
FBD of each member

29. 7.1 Internal Forces Developed in
Structural Members
Solution
Member AC
∑ MA = 0; -400kN(4m) + (3/5)FDC(8m)= 0
FDC = 333.3kN
+→∑ Fx = 0; -Ax + (4/5)(333.3kN) = 0
Ax = 266.7kN
+↑∑ Fy = 0; Ay – 400kN + 3/5(333.3kN) = 0
Ay = 200kN

30. 7.1 Internal Forces Developed in
Structural Members
Solution
FBD of segments AB and BC
Important to keep distributed loading
exactly as it is after the section is made

31. 7.1 Internal Forces Developed in
Structural Members
Solution
Member AB
+→∑ Fx = 0; NB – 266.7kN = 0
NB = 266.7kN
+↑∑ Fy = 0; 200kN – 200kN - VB = 0
VB = 0
∑ MB = 0; MB – 200kN(4m) – 200kN(2m) = 0
MB = 400kN.m

32. 7.1 Internal Forces Developed in
Structural Members
Example 7.5
Determine the normal force,
shear force and the bending
moment acting at point E of
the frame loaded.

33. 7.1 Internal Forces Developed in
Structural Members
Solution
Support Reactions
Members AC and CD are two force members
+↑∑ Fy = 0;
Rsin45° – 600N = 0
R = 848.5N

34. 7.1 Internal Forces Developed in
Structural Members
Solution
FBD of segment CE

35. 7.1 Internal Forces Developed in
Structural Members
Solution
+→∑ Fx = 0; 848.5cos45°N - VE = 0
VE = 600 N
+↑∑ Fy = 0; -848.5sin45°N + NE = 0
NE = 600 N
∑ ME = 0; 848.5cos45°N(0.5m) - ME = 0
ME = 300 N.m
Results indicate a poor design
Member AC should be straight to eliminate
bending within the member

36. 7.1 Internal Forces Developed in
Structural Members
Example 7.6
The uniform sign has a mass of
650kg and is supported on the fixed
column. Design codes indicate that
the expected maximum uniform
wind loading that will occur in the
area where it is located is 900Pa.
Determine the internal loadings at A

37. 7.1 Internal Forces Developed in
Structural Members
Solution
Idealized model for the sign
Consider FBD of a section above
A since it dies not involve the
support reactions
Sign has weight of
W = 650(9.81) = 6.376kN
Wind creates resultant force
Fw = 900N/m2(6m)(2.5m)
= 13.5kN

38. 7.1 Internal Forces Developed in
Structural Members
Solution
FBD of the loadings

39. 7.1 Internal Forces Developed in
Structural Members
Solution
r
∑ F = 0;
r r r
FA − 13.5i − 6.3475k = 0
r r r
FA = {13.5i + 6.38k }kN
r
∑ M A = 0;
r r r r
M A + r X ( Fw + W ) = 0
r r r
i j k
r
MA + 0 3 5.25 = 0
− 13.5 0 6.376
r r r r
M A = {−19.1i + 70.9 j + 40.5k }kN .m

40. 7.1 Internal Forces Developed in
Structural Members
Solution
FAz = {6.38k}kN represents the normal force N
FAx= {13.5i}kN represents the shear force
MAz = {40.5k}kN represents the torisonal moment
Bending moment is determined from
r r2 r2
M = Mx + My
where MAx = {-19.1i}kNm and MAy = {-70.9j}kN.m