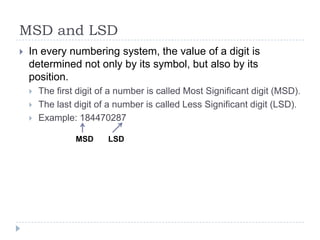
This document discusses numbering systems and conversions between systems. It defines base as the number of symbols used in a system and provides examples. The most and least significant digits in a number are defined based on their position. Binary addition and subtraction rules are covered. Methods for converting between decimal, binary, octal and hexadecimal systems are outlined, which involve repeatedly dividing by the base value and tracking the remainders or place values.

1. Module 5: Digital Techniques and
Electronic Instrument Systems
5.2 Numbering Systems

2. Number and Base
 Base: How many symbols (digits) are used in the
current numbering system?
 e.g. if the base of a number is 10, we use (maximum) 10
symbols to display this number.
 if the base of a number is 8, we use 8 symbols to display
this number. (0, 1, 2, 3, 4, 5, 6, 7).
 Examples: 1578, 1808210, 1001012.

3. MSD and LSD
 In every numbering system, the value of a digit is
determined not only by its symbol, but also by its
position.
 The first digit of a number is called Most Significant digit (MSD).
 The last digit of a number is called Less Significant digit (LSD).
 Example: 184470287
MSD LSD

4. Binary System Rules
 0 + 0 = 0
 1 + 0 = 1
 0 + 1 = 1
 1 + 1 = 0 and 1 carry.
 0 – 0 = 0
 1 – 0 = 1
 0 – 1 = 1 with 1 carry
 1 – 1 = 0
 Complementary
subtraction:
 Get the complementary
of the subtrahend.
 Add 1
 Make addition
 Discard any carries that
exceed the size of the
minuend.

5. Numbering System Conversions
 Decimal to digital:
 I divide the decimal number by 2
 I repeatedly divide the result by 2, until the dividend
becomes zero.
 The residue of each division in reverse order is the binary
number.
 Digital to decimal:
 In the first digit d0 of the binary number I assign d0 *20.
 In the nth digit of the binary number I assign dn *2n.
 The sum: d0*20+ d1*21 + … + dn*2n is the decimal number.
 Octal, Hex number conversion:
 The same methodology, but “2” is replaced with “8” and
“16” respectively.