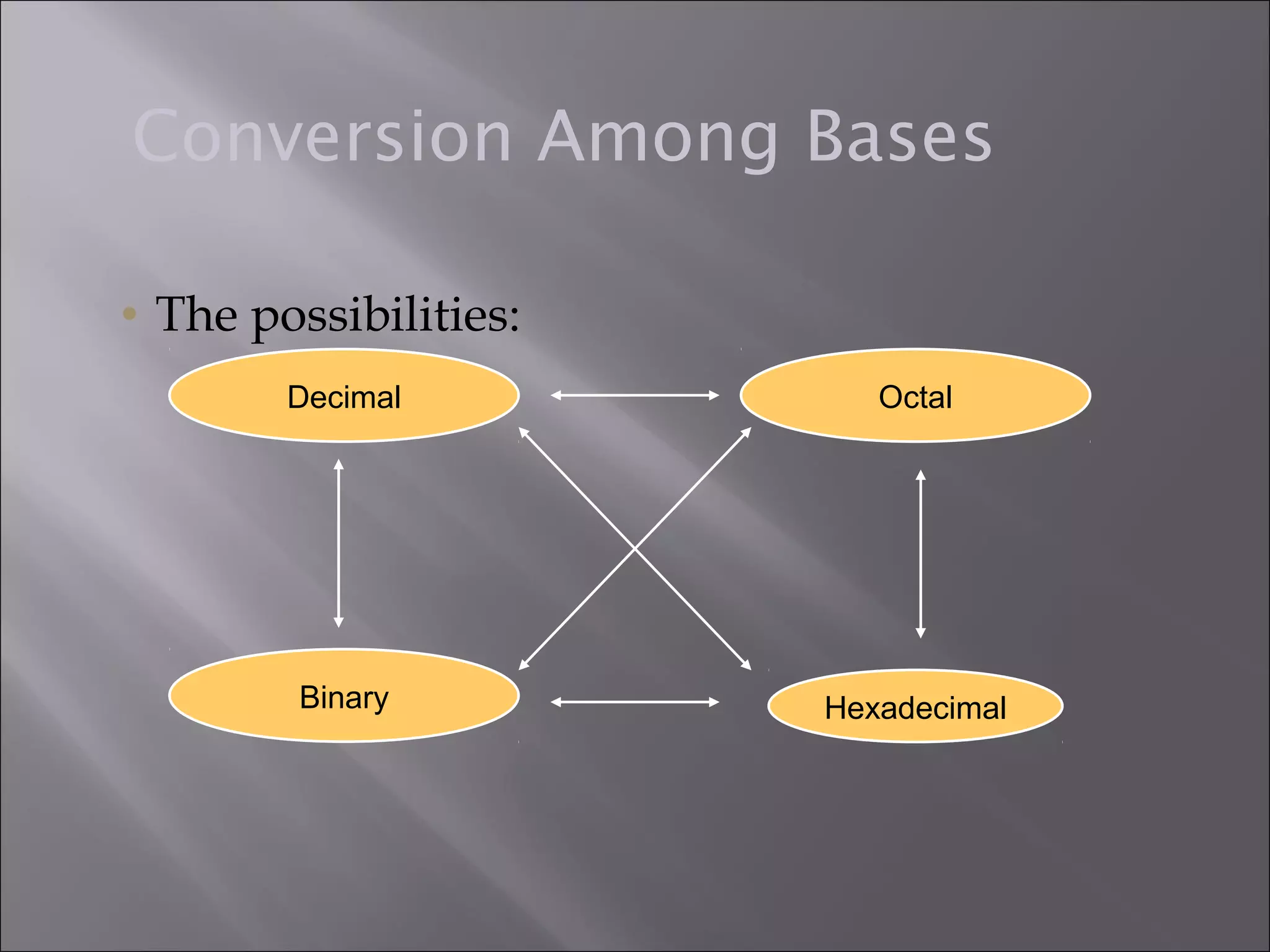
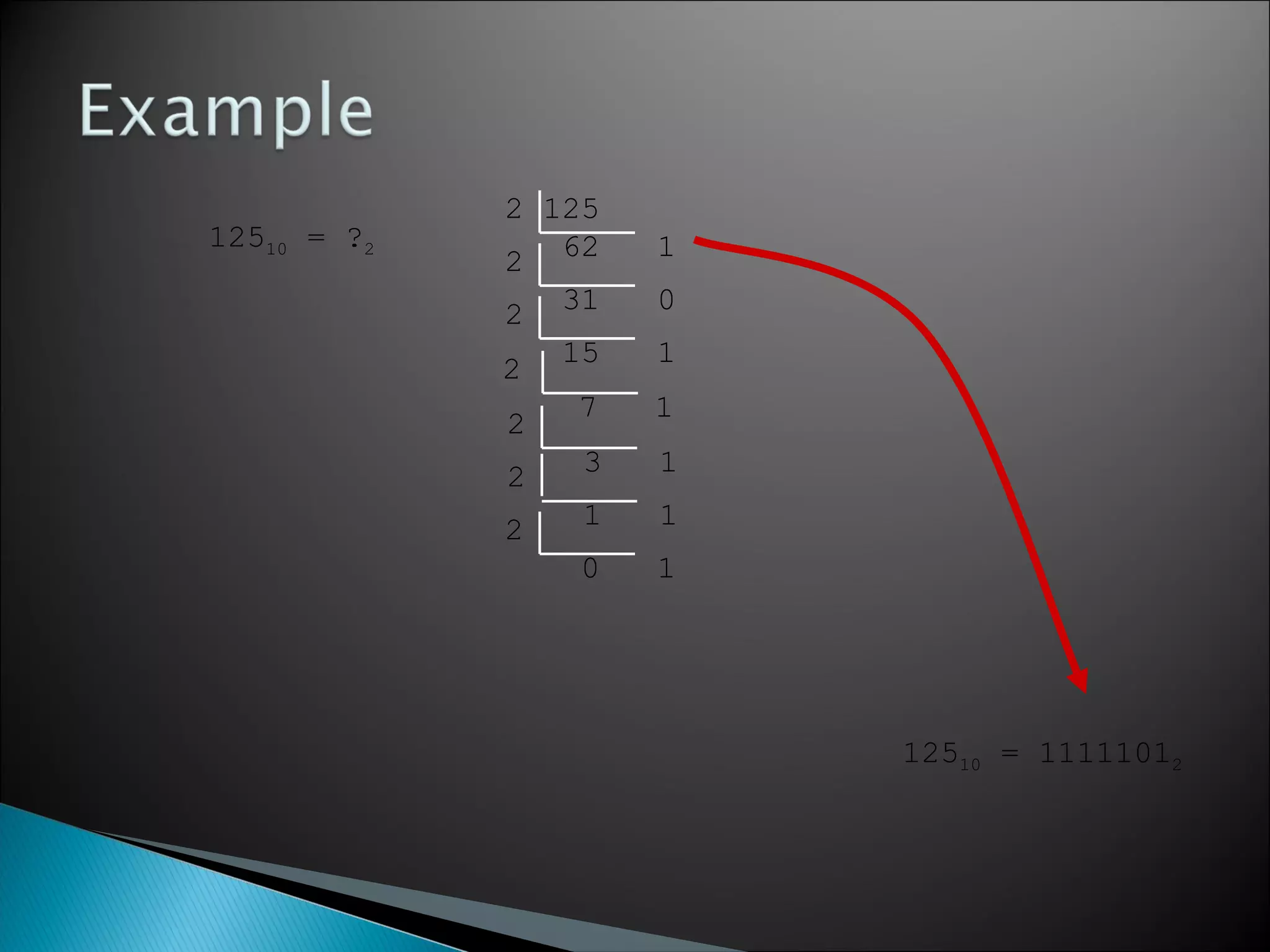
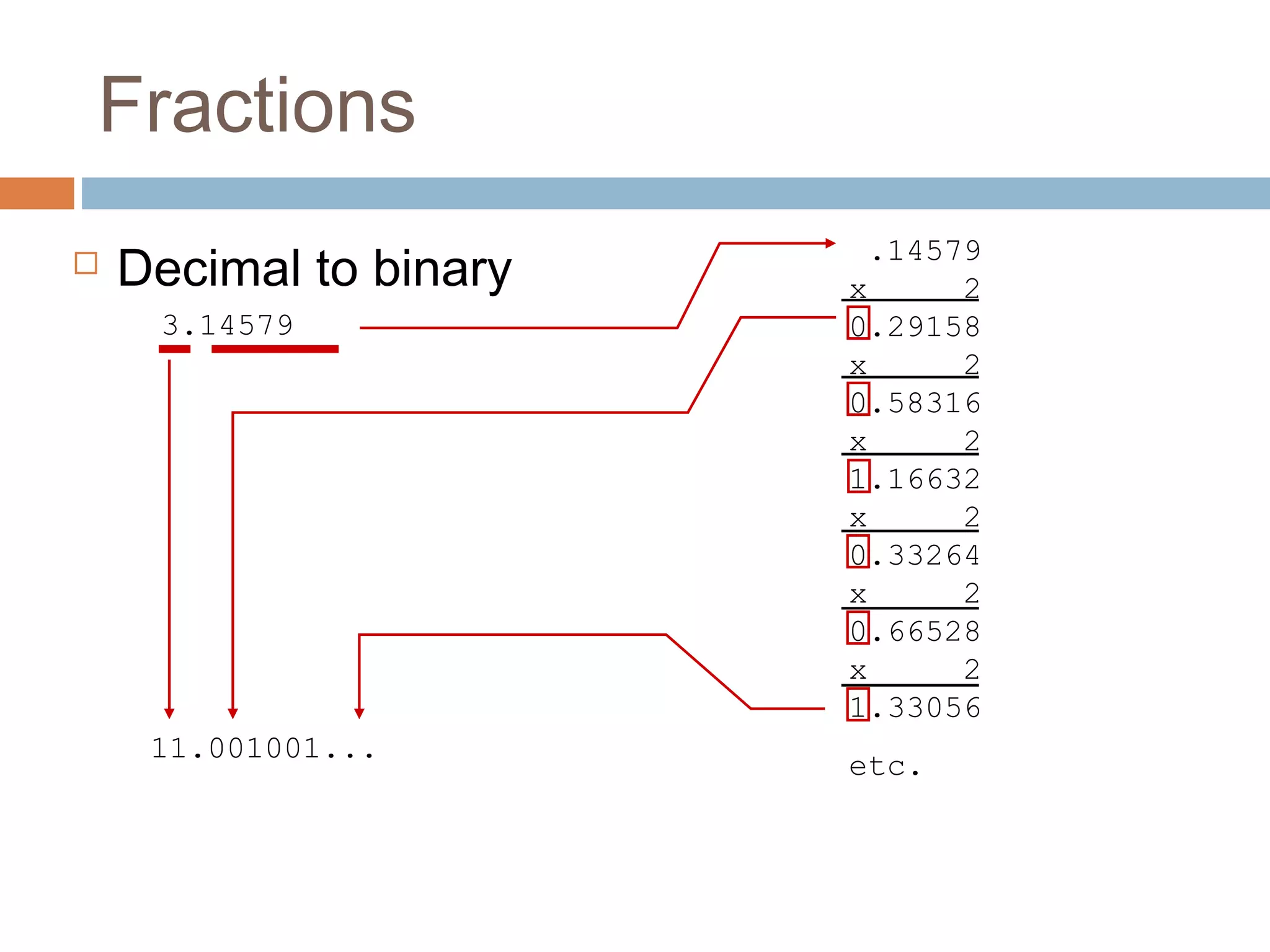
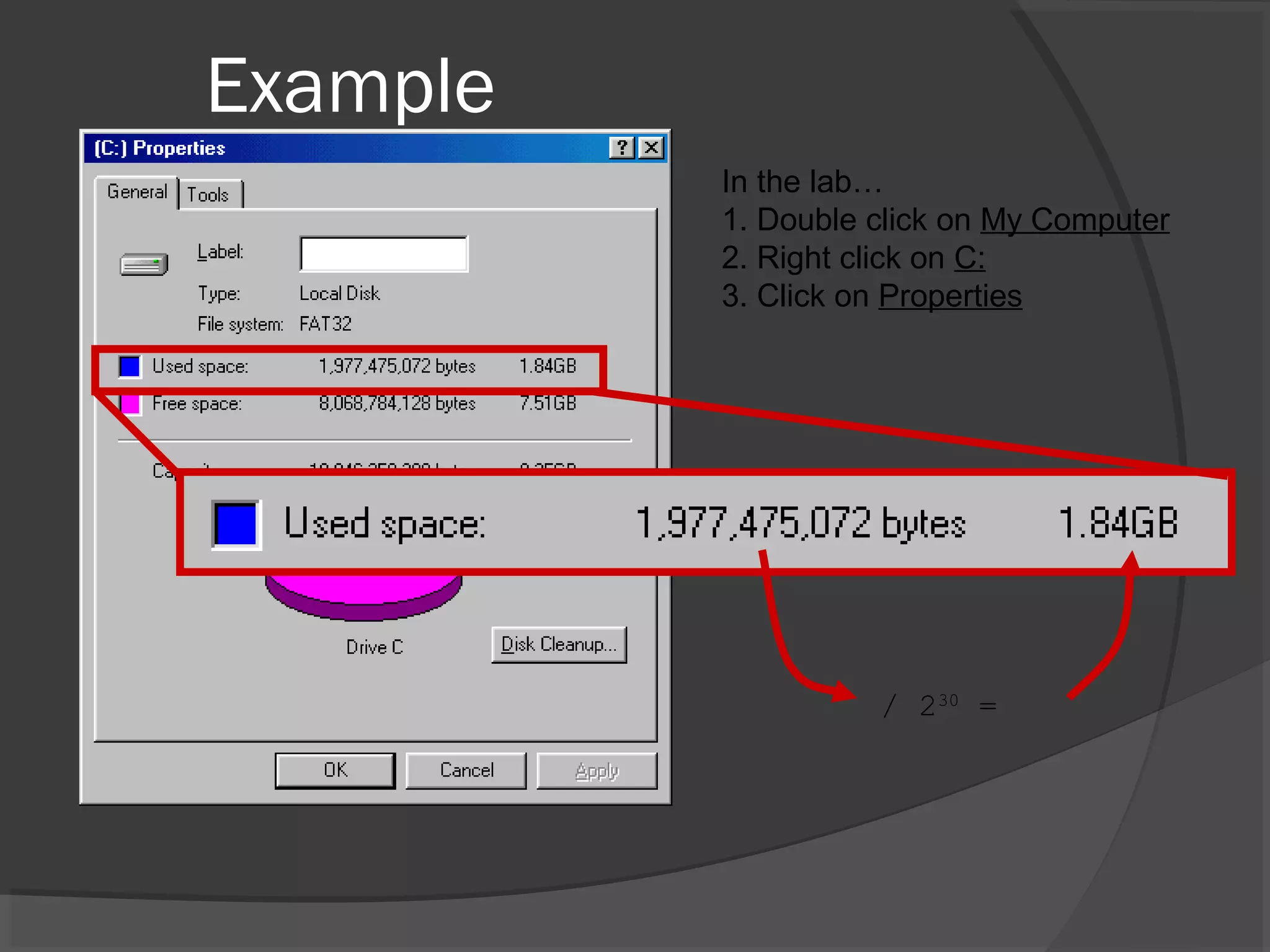
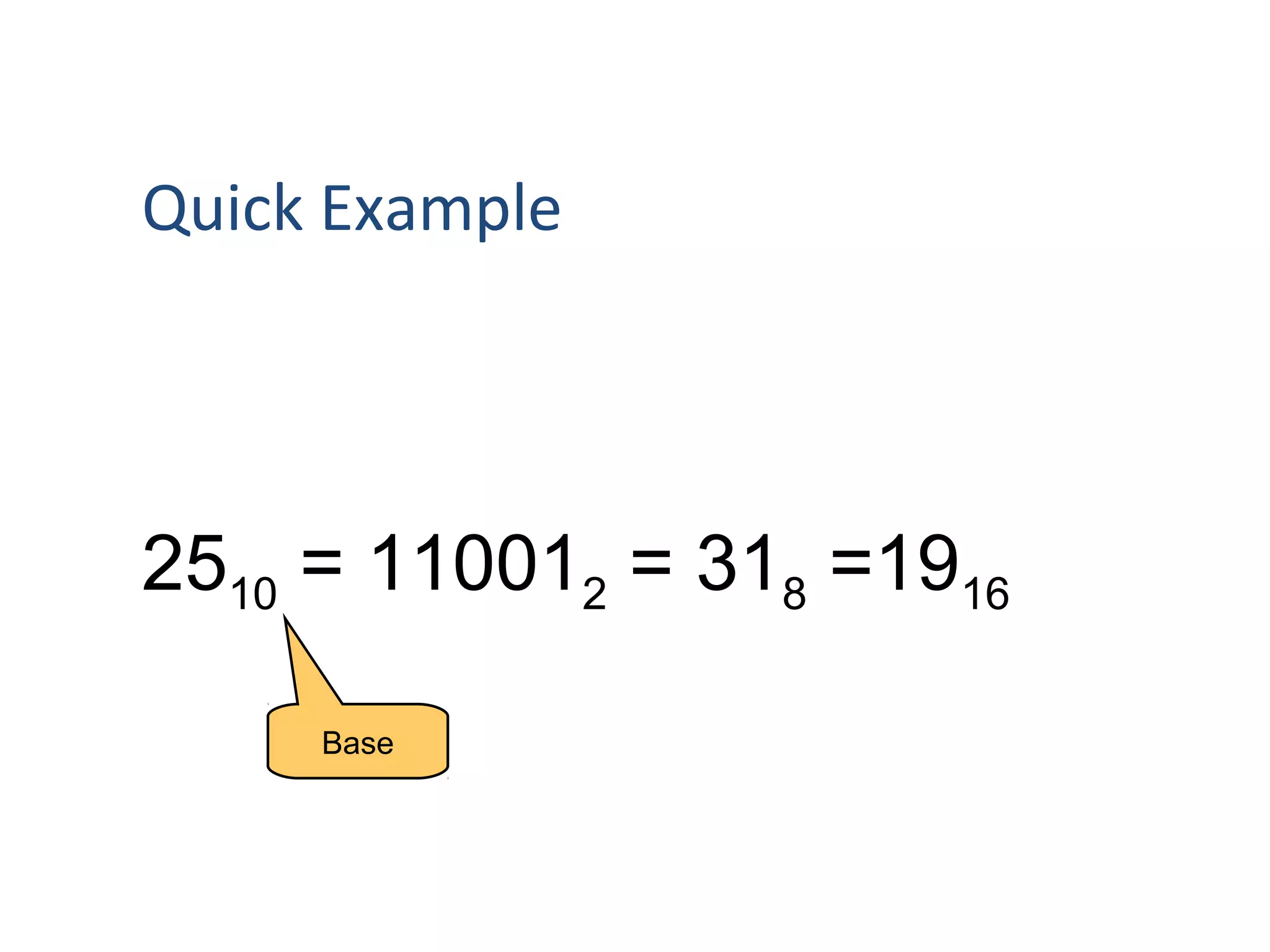The document explores various number systems, particularly the decimal and binary systems, and their uses in mathematics and computing. It acknowledges contributors to the project and discusses base conversions and techniques for different numeral systems, including examples. It emphasizes the significance of understanding numbers and encourages exploration of their complexities.

1. NNUUMMBBEERR
SSYYSSTTEEMM
22
The mysterious world of numbers…

2. Acknowledgement
We would like to thank AKP sir for giving us an
opportunity to express ourselves on this enthusiastic
project. Any accomplishment requires the effort of
many people and this work is no different. Every group
member has been an important part of this project. We
also thank our friends for their ideas and co-operation
they provided to us. We are grateful to all of them.
Thank you..

3.  A number is a mathematical object used in
counting and measuring. Numerals are often used for
labels, for ordering serial numbers, and for codes like
ISBNs.
 In mathematics, the definition of number has been
extended over the years to include such numbers as zero,
negative numbers, rational numbers, irrational numbers,
and complex numbers.

4. The number system we use on day-to-day basis
in the decimal system , which is based on ten
digits: zero through nine. As the decimal system
is based on ten digits, it is said to be base -10 or
radix-10. Outside of specialized requirement
such as computing , base-10 numbering system
have been adopted almost universally. The
decimal system with which we are fated is a
place-value system, which means that the
value of a particular digit depends both on the
itself and on its position within the number.

5.  The binar y numeral system, or base-2 number
system, represents numeric values using two symbols, 0 and
1. More specifically, the usual base-2 system is a positional
notation with a radix of 2. Owing to its straight forward
implementation in digital electronic circuitry using logic
gates, the binary system is used internally by all modern
computers.
 Counting in binary is similar to counting in any other
number system. Beginning with a single digit, counting
proceeds through each symbol, in increasing order. Decimal
counting uses the symbols 0 through 9, while binary only
uses the symbols 0 and 1.

6. Archimedes :
He was a Greek mathematician. He was the first to
compute the digits in the decimal expansion of π (pi). He
showed that -
3.140845 < π < 3.142857
Archimedes

7. Conversion Among Bases
• The possibilities:
Decimal Octal
Hexadecimal
Binary

8. Quick Example
2510 = 110012 = 318 =1916
Base

9. > Binary to decimal
> Octal to decimal
> Hexadecimal to decimal
> Decimal to binary
> Octal to binary
> Hexadecimal to binary
> Decimal to octal, etc..
DDiiffffeerreenntt ccoonnvveerrssiioonnss ppoossssiibbllee::

10.  Technique
◦ Multiply each bit by 2n, where n is the “weight” of the bit
◦ The weight is the position of the bit, starting from 0 on
the right
◦ Add the results

11. 1010112 => 1 x 20 = 1
1 x 21 = 2
0 x 22 = 0
1 x 23 = 8
0 x 24 = 0
1 x 25 = 32
4310
Bit “0”

12. OOccttaall ttoo DDeecciimmaall
Technique
◦ Multiply each bit by 8n, where n is the “weight”
of the bit
◦ The weight is the position of the bit, starting
from 0 on the right
◦ Add the results

13. 7248 => 4 x 80 = 4
2 x 81 = 16
7 x 82 = 448
46810

14. Technique
Multiply each bit by 16n, where n is the “weight” of the
bit
The weight is the position of the bit, starting from 0 on
the right
Add the results

15. ABC16 => C x 160 = 12 x 1 = 12
B x 161 = 11 x 16 = 176
A x 162 = 10 x 256 = 2560
274810

16. Technique
Divide by two, keep track of the remainder
First remainder is bit 0 (LSB, least-significant bit)
Second remainder is bit 1
Etc.

17. 12510 = ?2
2 125
2 6 2 1
2 3 1 0
2 1 5 1
2 7 1
2 3 1
2 1 1
0 1
12510 = 11111012

18. Fractions
 Decimal to binary
3.14579
.14579
x 2
0.29158
x 2
0.58316
x 2
1.16632
x 2
0.33264
x 2
0.66528
x 2
1.33056
11.001001... etc.

19. OOccttaall ttoo BBiinnaarryy
Technique
◦ Convert each octal digit to a 3-bit equivalent
binary representation
EExxaammppllee
7058 = ?2
7 0 5
111 000 101
7058 = 1110001012

20. Technique
Convert each hexadecimal digit to a 4-bit equivalent
binary representation

21. 10AF16 = ?2
1 0 A F
0001 0000 1010 1111
10AF16 =
00010000101011112

22. Common Powers (2 of 2)
Base 2
Power Preface Symbol
210 kilo k
220 mega M
230 Giga G
Value
1024
1048576
1073741824
What is the value of “k”, “M”, and “G”?
I n comput ing, par t icular ly w.r .t . memor t he base-2 int er pr et at ion gener ally applies

23. Example
In the lab…
1. Double click on My Computer
2. Right click on C:
3. Click on Properties
/ 230 =

24. Numbers are never ending. You look into it, you find a
world of quantities, helping you in your daily chores.
It’s a simple yet hard to understand, you work on it,
you are going to love it more and more.
Exploring it is the best option, so just enjoy it.

26. Project made and Compiled by
~
Sanjana Poddar
Sana Jahan
Ronodeep Mazumdar
Riya Debnath