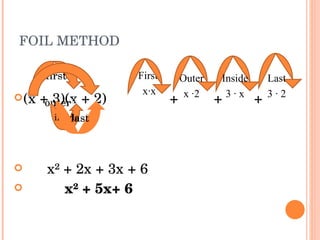
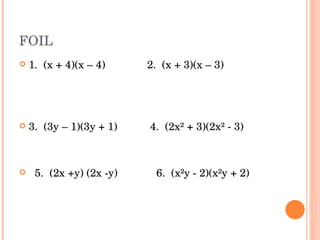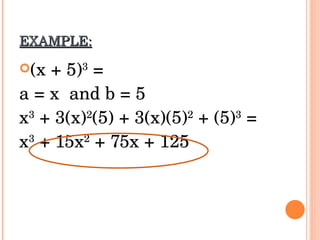The document provides examples and explanations of adding, subtracting, multiplying, and expanding polynomials. It demonstrates multiplying polynomials using the FOIL (First, Outer, Inner, Last) method and provides examples of sum and difference of squares, square of a binomial, cube of a binomial, and multiplying three binomials. Common patterns that arise when multiplying polynomials are identified.

1. ADDING, SUBTRACTING, & MULTIPLYING POLYNOMIALS

2. ERROR ANALYSIS A student simplified 6a³ -a³ and got a 6 as a result. Write an explanation of the student’s error using the words coefficient and like terms.

3. CHALLANGE A 35-centimeter stick is cut into three pieces so that the two end pieces are each equal in length to one-third of the middle piece. How long is each piece?

4. MULTIPLYING POLYNOMIALS 3a(6b + 7) (3a)(6b) + (3a)(7) 18ab + 21a 2x(3x² + x – 4) (2x)(3x²) + (2x)(x) + (2x)(-4) 6x³ + 2x² + -8x

5. YOUR TURN -4a²(-2a² + 3ab – 2b + 5)

6. MULTIPLYING BINOMIALS (x + 2)(x + 3) x(x+ 3) + 2(x + 3) (x)( x)+ (x)(3) + 2(x) + 2(3) x² + 3x + 2x + 6 x² + 5x + 6

7. FOIL METHOD (x + 3)(x + 2) + + + x² + 2x + 3x + 6 x² + 5x+ 6 first 2) outer (x inside last First x·x Outer x ·2 Inside 3 · x Last 3 · 2

8. YOUR TURN – USE FOIL METHOD 1. (x + 4)(x - 3) 2. (2x + 2)(x + 6) 3. (3ab² + b)(-2ab² - b) 4. (4xy + 3)(2x²y + 1)

9. FOIL 1. (x + 4)(x – 4) 2. (x + 3)(x – 3) 3. (3y – 1)(3y + 1) 4. (2x² + 3)(2x² - 3) 5. (2x +y) (2x -y) 6. (x²y - 2)(x²y + 2)

10. FOIL 1.(y + 1)(y + 1) 2. (x + 2)² 3. (2x - 3)² 4. .(y² + 1)² 5.(2x – y)² 6. .(2y² - 2x)²

11. SOME BINOMIAL PRODUCTS APPEAR SO MUCH WE NEED TO RECOGNIZE THE PATTERNS! Sum & Difference (S&D): (a + b)(a – b) = a 2 – b 2 Example: (x + 3)(x – 3) = x 2 – 9 Square of Binomial: (a + b) 2 = a 2 + 2ab + b 2 (a - b) 2 = a 2 – 2ab + b 2

12. MULTIPLYING POLYNOMIALS : HORIZONTALLY (3x 2 – 2x – 4)(x – 3) = (3x 2 )(x – 3) + (-2x)(x – 3) + (-4)(x – 3) = (3x 3 – 9x 2 ) + (-2x 2 + 6x) + (-4x + 12) = 3x 3 – 9x 2 – 2x 2 + 6x – 4x +12 = 3x 3 – 11x 2 + 2x + 12

13. MULTIPLYING POLYNOMIALS: VERTICALLY (-x 2 + 2x + 4)(x – 3)= -x 2 + 2x + 4 * x – 3 3x 2 – 6x – 12 -x 3 + 2x 2 + 4x_____ -x 3 + 5x 2 – 2x – 12

14. MULTIPLYING 3 BINOMIALS : (x – 1)(x + 4)(x + 3) = FOIL the first two: (x 2 – x +4x – 4)(x + 3) = (x 2 + 3x – 4)(x + 3) = Then multiply the trinomial by the binomial (x 2 + 3x – 4)(x) + (x 2 + 3x – 4)(3) = (x 3 + 3x 2 – 4x) + (3x 2 + 9x – 12) = x 3 + 6x 2 + 5x - 12

15. LAST PATTERN Cube of a Binomial (a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3 (a – b) 3 = a 3 - 3a 2 b + 3ab 2 – b 3

16. EXAMPLE: (x + 5) 3 = a = x and b = 5 x 3 + 3(x) 2 (5) + 3(x)(5) 2 + (5) 3 = x 3 + 15x 2 + 75x + 125