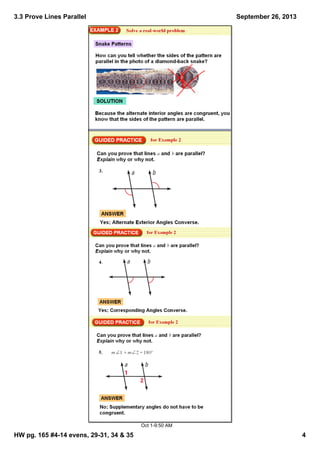
This document contains notes from a geometry class on proving that lines are parallel. It includes definitions of key postulates and theorems used to prove parallel lines, such as corresponding angles being congruent, alternate interior angles being congruent, and consecutive interior angles being supplementary. Examples are worked through to demonstrate these concepts. Homework problems from the textbook are assigned.

1. 3.3 Prove Lines Parallel
HW pg. 165 #4­14 evens, 29­31, 34 & 35 1
September 26, 2013
Sep 24­2:59 PM
Bellwork
With your partner, stand in the center of
the room according to the angle pair card
you receive.
Determine whether your angles are
congruent or supplementary.
One partner is to hold the angle pair card,
and the other partner will hold the = card,
(located on the front desk).

2. 3.3 Prove Lines Parallel
HW pg. 165 #4­14 evens, 29­31, 34 & 35 2
September 26, 2013
Oct 1­8:35 AM
3.3 Prove Lines are Parallel
Postulate 16: Corresponding Angles Converse
If 2 lines are cut by a transversal so the corresponding
angles are congruent, then the lines are parallel.
Example 1
Find the value of x that makes m // n.
Guided Practice #1 with partners
m
n65
(3x + 5)
6 k
2 j
j // k

3. 3.3 Prove Lines Parallel
HW pg. 165 #4­14 evens, 29­31, 34 & 35 3
September 26, 2013
Oct 1­9:17 AM
Theorem 3.4: Alternate Interior Angles Converse
If 2 lines are cut by a transversal so the alternate interior
angles are congruent, then the lines are parallel.
Theorem 3.5: Alternate Exterior Angles Converse
If 2 lines are cut by a transversal so the alternate exterior
angles are congruent, then the lines are parallel.
Theorem 3.6: Consecutive Interior Angles Converse
If 2 lines are cut by a transversal so the consecutive
interior angles are supplementary, then the lines are parallel.
k
45
jj // k
j // k
j // k
j
k
1
8
3
5
j
k
<3+<5=180

4. 3.3 Prove Lines Parallel
HW pg. 165 #4­14 evens, 29­31, 34 & 35 4
September 26, 2013
Oct 1­9:50 AM

5. 3.3 Prove Lines Parallel
HW pg. 165 #4­14 evens, 29­31, 34 & 35 5
September 26, 2013
Oct 1­9:51 AM

6. 3.3 Prove Lines Parallel
HW pg. 165 #4­14 evens, 29­31, 34 & 35 6
September 26, 2013
Oct 1­10:03 AM
Paragraph Proof: written in paragraph form and in sentences
explaining the logical flow of argument

7. 3.3 Prove Lines Parallel
HW pg. 165 #4­14 evens, 29­31, 34 & 35 7
September 26, 2013
Oct 1­10:11 AM
Theorem 3.7: Transitive Property of Parallel Lines
If 2 lines are parallel to the same line,
then they are parallel to each other.

8. 3.3 Prove Lines Parallel
HW pg. 165 #4­14 evens, 29­31, 34 & 35 8
September 26, 2013
Oct 1­10:02 AM
HW pg. 165
#4­14 evens
29­31,
34 & 35