Recommended
PPTX
2.Бүлэглэлт, Тархалтын цуваа байгуулах
PPTX
Хугацааны цуваан шинжилгээ
PDF
PPT
PPTX
Д.БА206 СТАТИСТИК ХЭМЖИГДЭХҮҮН
PDF
Lekts5 tarhaltiin tsuvaanii dundaj, helbelzliin uzuuleltuud
PDF
Lekts13. dinamik egnee jisheetei buten
PDF
DOC
PDF
ТООН МЭДЭЭЛЭЛД ДҮН ШИНЖИЛГЭЭ ХИЙХ ГАРЫН АВЛАГА
PDF
PDF
PPTX
инфляцийн хурдыг багасгах оновчтой арга замууд
PPTX
PDF
National calculation systems
PDF
PPTX
PDF
PDF
PPTX
PDF
Эрэлт, нийлүүлэлтийн мэдрэмж /орлогын мэдрэмж, солбисон мэдрэмж/
PPTX
PPTX
санхүүгийн зах зээл, ббсб
PDF
микро эдийн засаг : судлах зүйл, судалгааны арга
PPTX
PPTX
PPTX
PPT
Business statistics processing
PDF
To rs middle income group in mic_mon_final
PPT
More Related Content
PPTX
2.Бүлэглэлт, Тархалтын цуваа байгуулах
PPTX
Хугацааны цуваан шинжилгээ
PDF
PPT
PPTX
Д.БА206 СТАТИСТИК ХЭМЖИГДЭХҮҮН
PDF
Lekts5 tarhaltiin tsuvaanii dundaj, helbelzliin uzuuleltuud
PDF
Lekts13. dinamik egnee jisheetei buten
PDF
What's hot
DOC
PDF
ТООН МЭДЭЭЛЭЛД ДҮН ШИНЖИЛГЭЭ ХИЙХ ГАРЫН АВЛАГА
PDF
PDF
PPTX
инфляцийн хурдыг багасгах оновчтой арга замууд
PPTX
PDF
National calculation systems
PDF
PPTX
PDF
PDF
PPTX
PDF
Эрэлт, нийлүүлэлтийн мэдрэмж /орлогын мэдрэмж, солбисон мэдрэмж/
PPTX
PPTX
санхүүгийн зах зээл, ббсб
PDF
микро эдийн засаг : судлах зүйл, судалгааны арга
PPTX
PPTX
PPTX
PPT
Business statistics processing
Viewers also liked
PDF
To rs middle income group in mic_mon_final
PPT
PDF
Regression and time series
PDF
PPTX
Oyutnii setgel hanamjiin sudalgaa
PDF
PDF
PDF
PDF
Ulirliin nuluulultei hugatsaanii tsuvaag tegshitgeh
PPT
PDF
PDF
PPT
PPT
PPT
PPTX
PPTX
PPT
Session 1 introduction to valuation
PDF
PDF
Similar to 3 numerical descriptive measures
PDF
Lecture_4_Numerical_Descriptive_Measures.pdf
PDF
PPTX
DOCX
machine learningsahfahsfahsfashfsahfsahfsahjf
PPT
PPTX
PDF
эрүүл мэндийн статистик лекц 1
PDF
эрүүл мэндийн статистик лекц 1
PPT
DOCX
DOCX
DOCX
PDF
PDF
эрүүл мэндийн статистик лекц 1
PDF
PDF
PDF
PPT
2 presenting data in tables and charts
PDF
эрүүл мэндийн статистик лекц
PDF
Lekts4. statistik hemjigdehuun
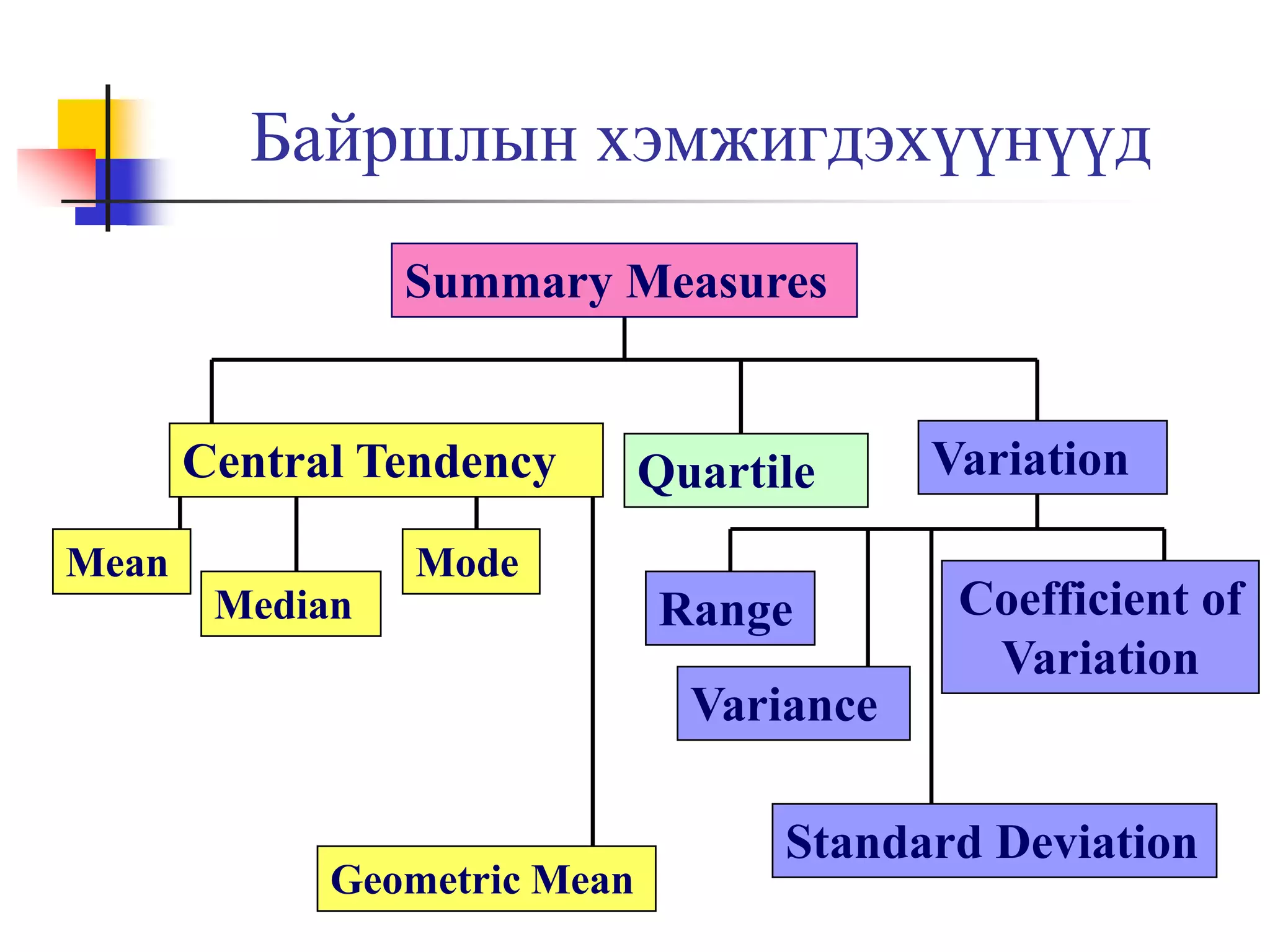
3 numerical descriptive measures 1. 2. Сэдвийн гарчиг
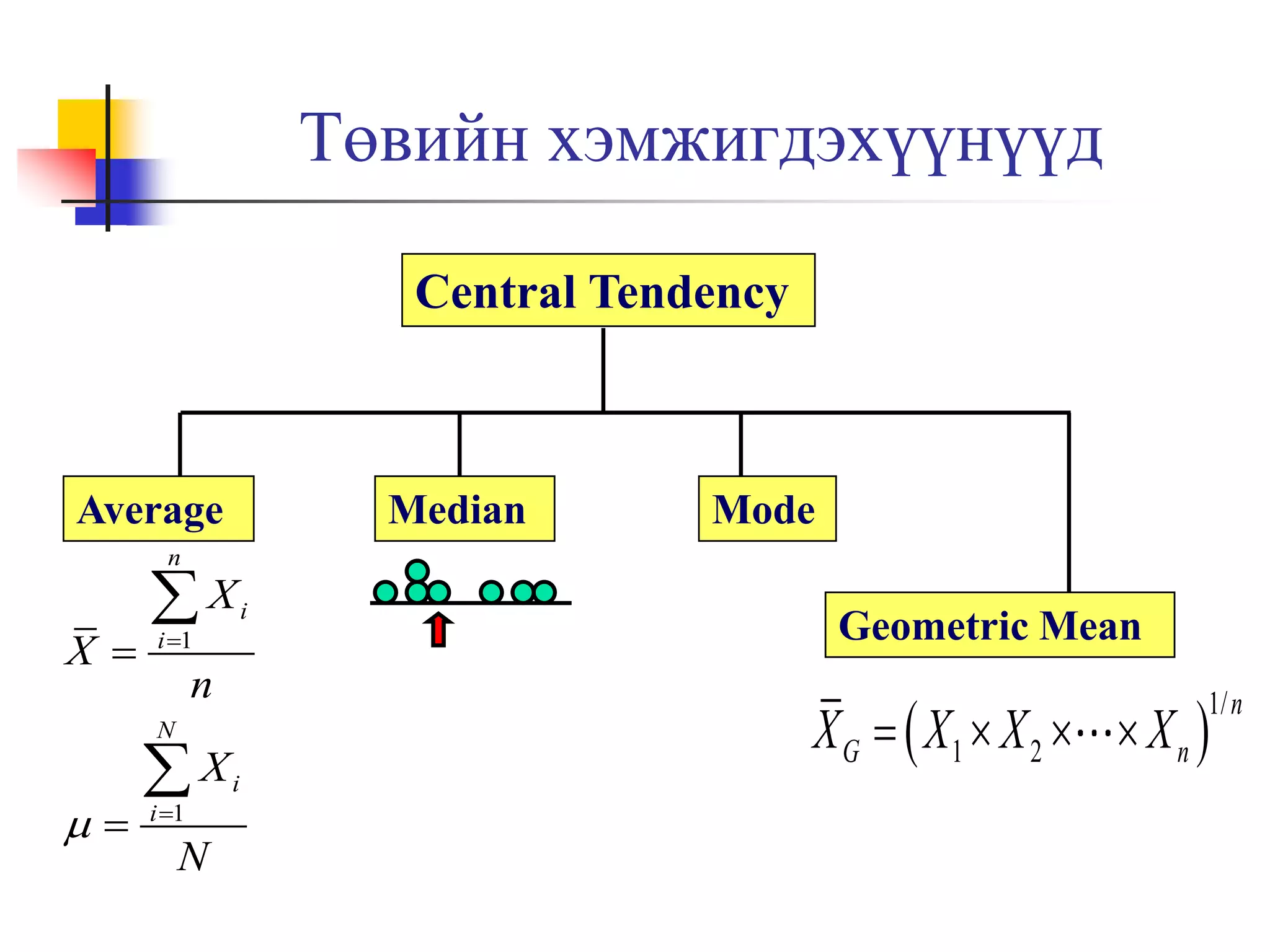
Төвийн хэмжигдэхүүн
Арифметик дундаж, медиан, мода, геометр дундаж,
midrange
Квартил
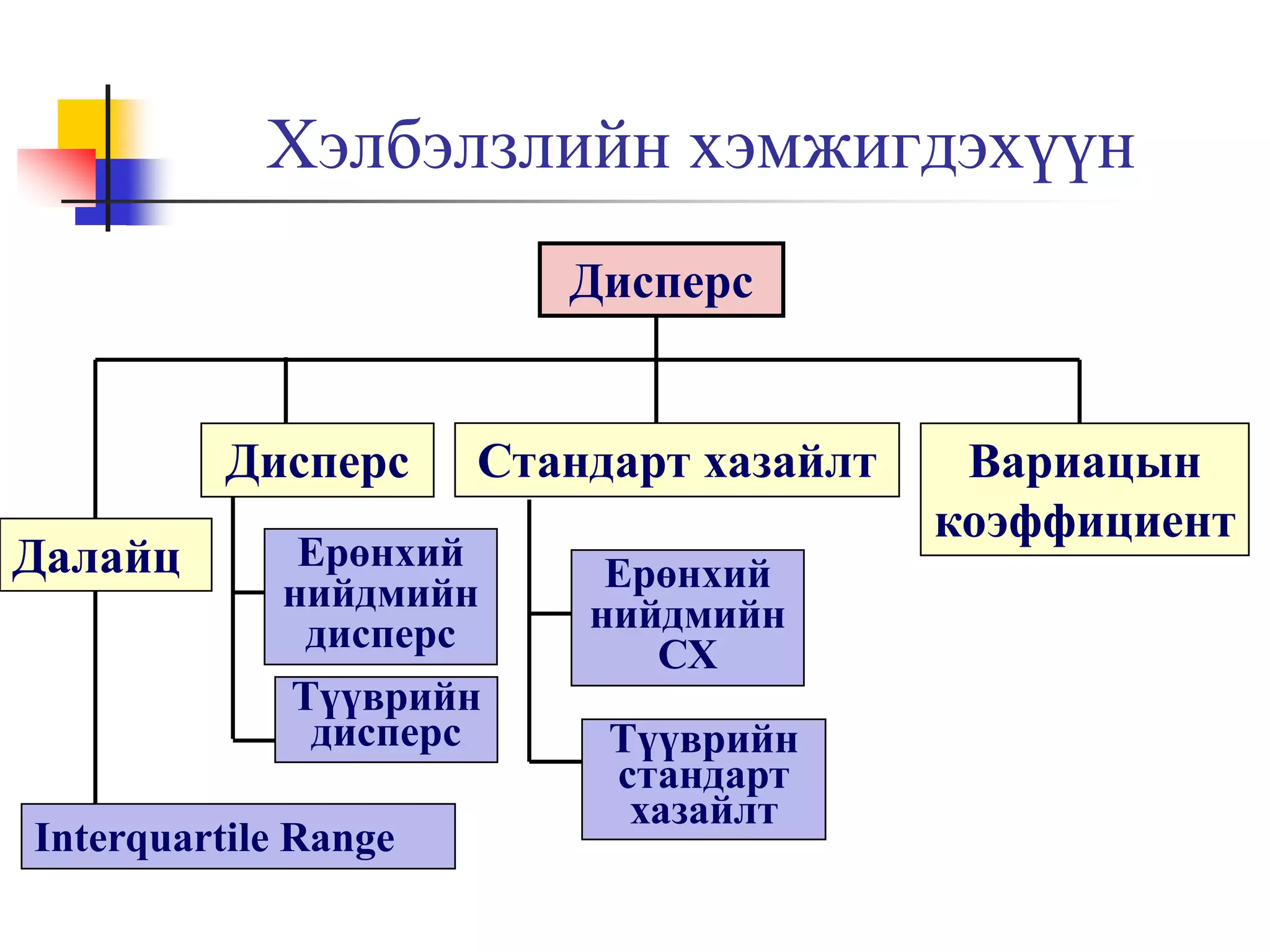
Хэлбэлзлийн хэмжигдэхүүн
Далайц, Interquartile range, дисперс ба стандарт
хазайлт, вариацийн коэффициент
Хэлбэр
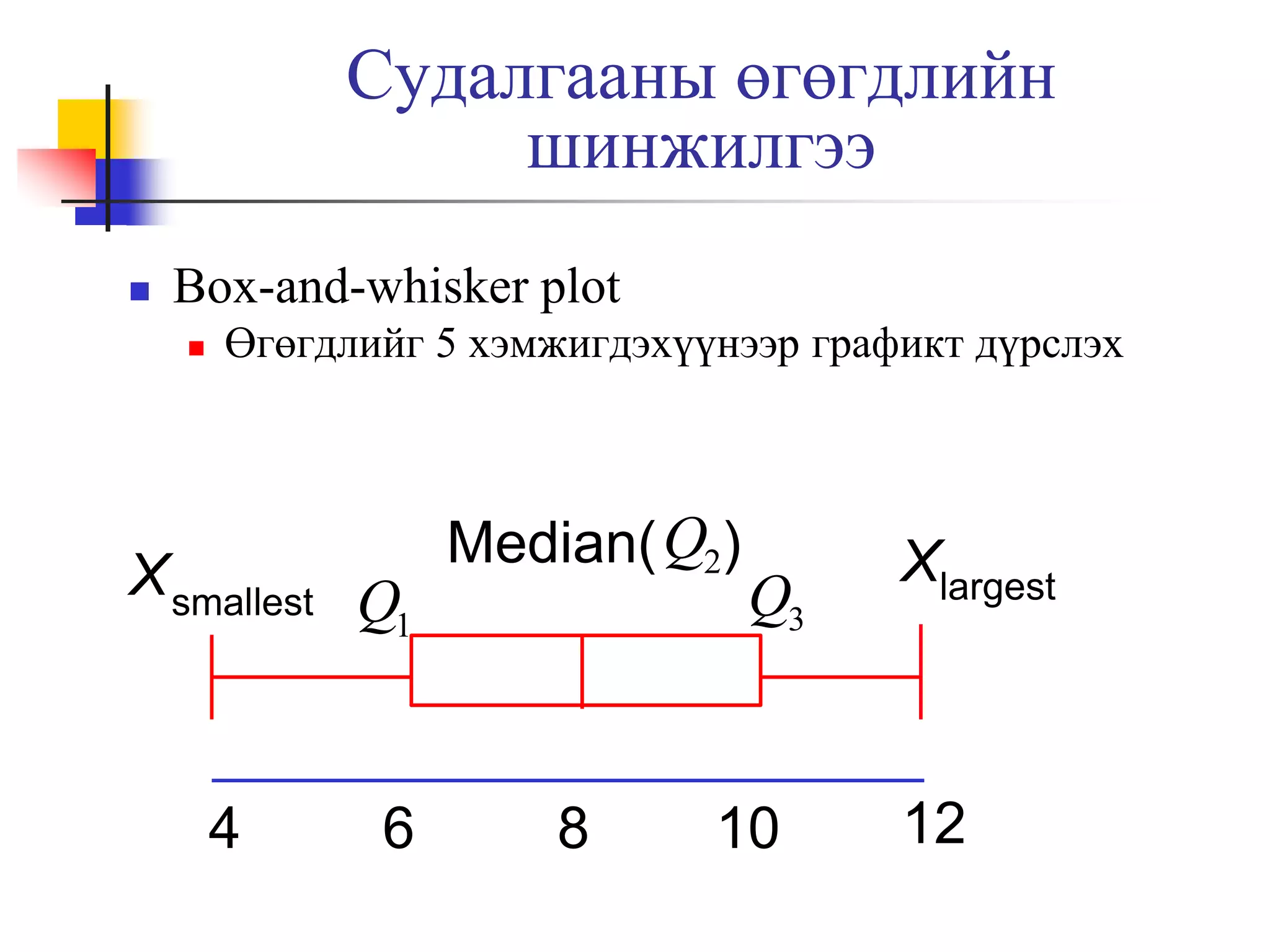
Symmetric, skewed, box-and-whisker plot ашиглах
3. 4. 5. 6. Дундаж хэмжигдэхүүн нь зэргээсээ
хамаарч дараах хэлбэрүүдтэй
Зэрэг
илтгэгч
Дундаж
-1
Гармоник
0
Геометр
1
Арифметик
Жинлэгдсэн
f
f
x
xr
xr
x geo x1f1 x2f 21 xnfn1
f
xf
f
xa
Жинлэгдээгүй
1
x
x geo n x1 x2 xn
xa
x f
f
n
x
n
2
2
Квадрат
xa
x
xa
x f
f
n
3
3
Куб
xa 3
xa
2
3
x
n
3
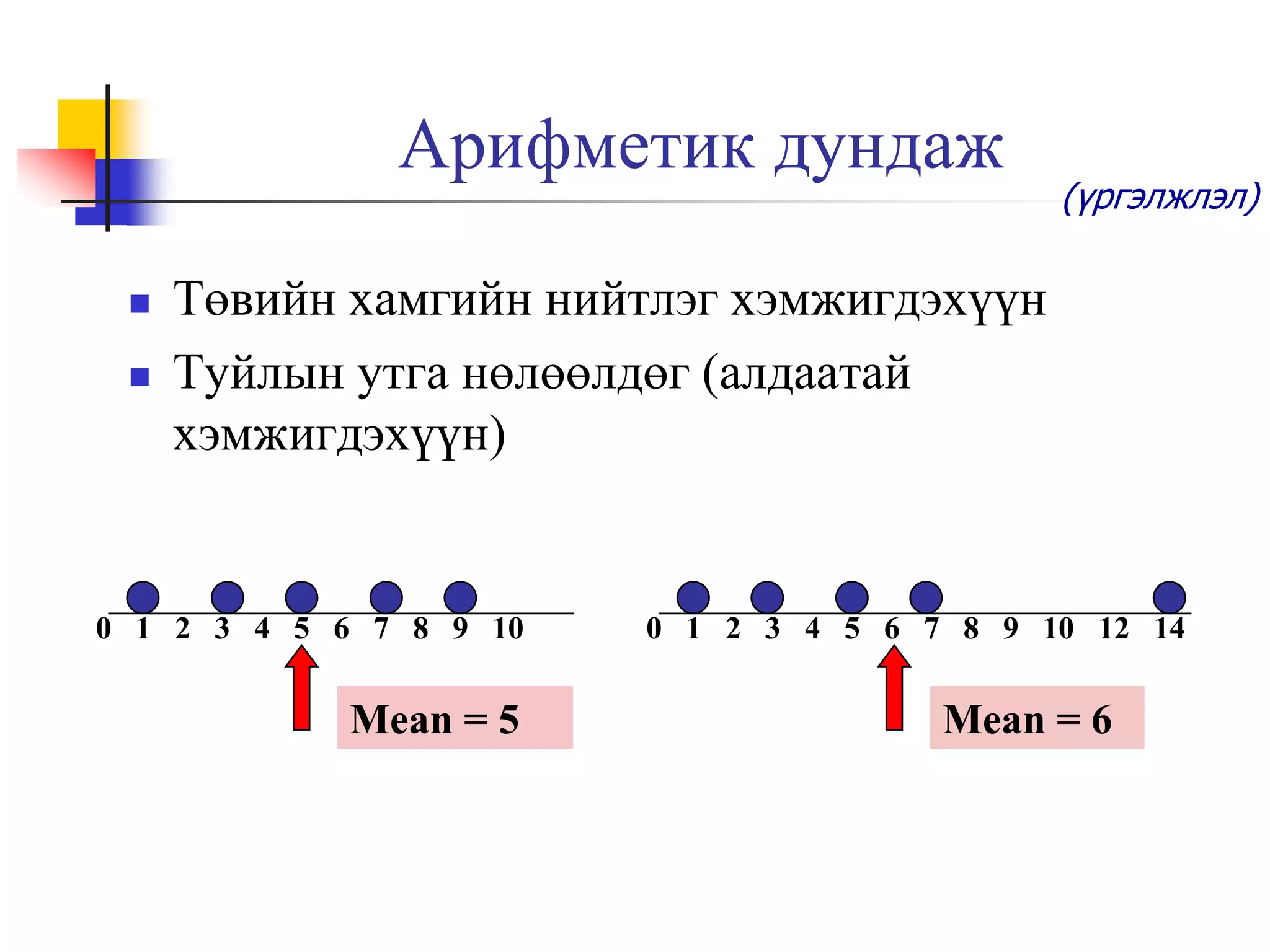
7. Арифметик дундаж
Өгөгдлийн арифметик дундаж
Түүврийн дундаж
n
X
X
i 1
i
n
Түүврийн хэмжээ
X1 X 2
n
Xn
X1 X 2
N
XN
Ерөнхий нийдмийн дундаж
Ерөнхий нийдмийн хэмжээ
N
X
i 1
N
i
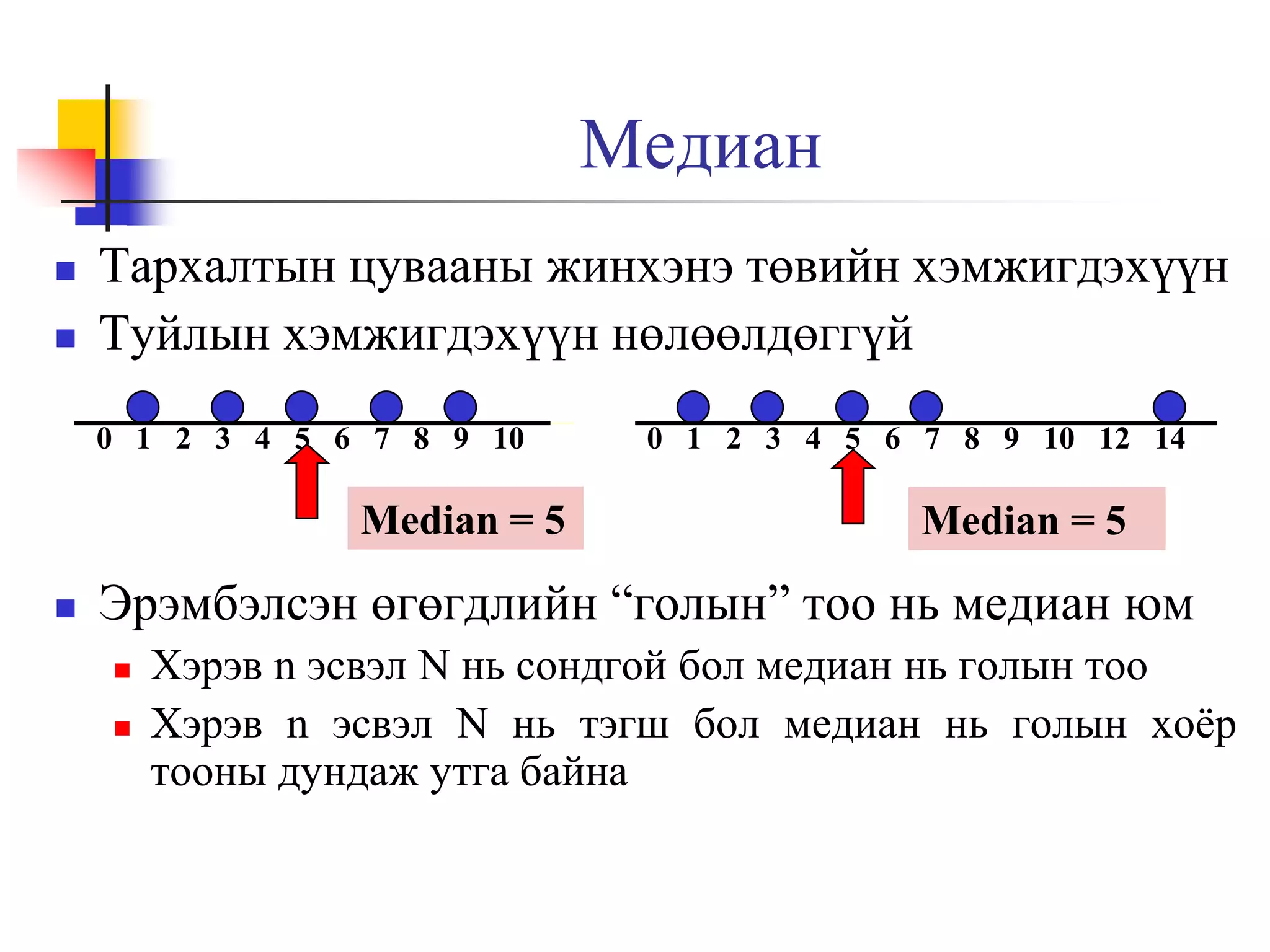
8. 9. Медиан
Тархалтын цувааны жинхэнэ төвийн хэмжигдэхүүн
Туйлын хэмжигдэхүүн нөлөөлдөггүй
0 1 2 3 4 5 6 7 8 9 10
Median = 5
0 1 2 3 4 5 6 7 8 9 10 12 14
Median = 5
Эрэмбэлсэн өгөгдлийн “голын” тоо нь медиан юм
Хэрэв n эсвэл N нь сондгой бол медиан нь голын тоо
Хэрэв n эсвэл N нь тэгш бол медиан нь голын хоёр
тооны дундаж утга байна
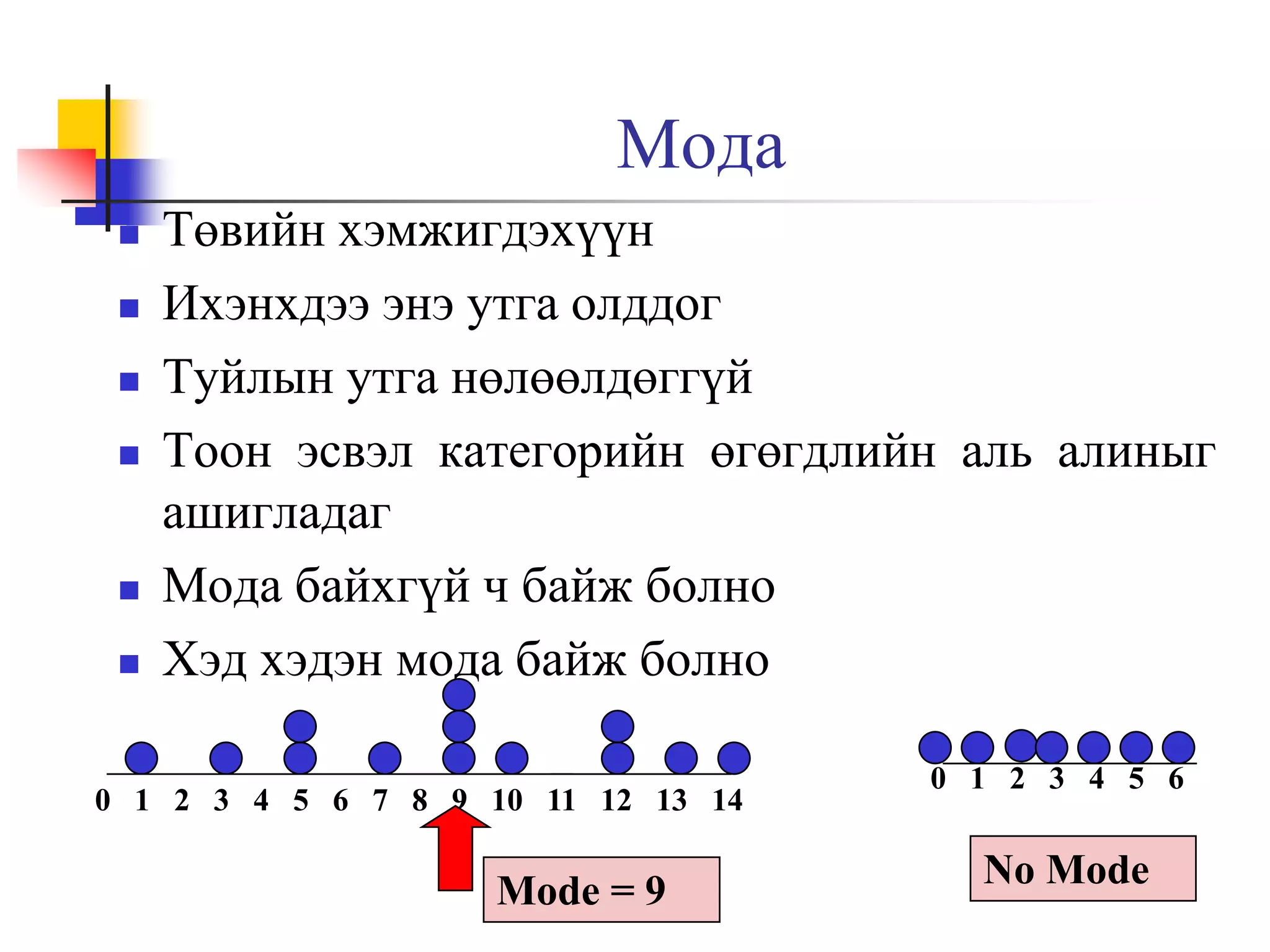
10. Мода
Төвийн хэмжигдэхүүн
Ихэнхдээ энэ утга олддог
Туйлын утга нөлөөлдөггүй
Тоон эсвэл категорийн өгөгдлийн аль алиныг
ашигладаг
Мода байхгүй ч байж болно
Хэд хэдэн мода байж болно
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
Mode = 9
0 1 2 3 4 5 6
No Mode
11. Геометр дундаж
Хувьсагчийн цаг хугацаан дахь
өөрчлөлтийг хэмжихэд ашигладаг
X G X1 X 2
хувиарх
Xn
1/ n
Өгөөжийн нормын геометр дундаж
Хөрөнгө оруулалтын цаг хугацаан дахь төлвийг
хэмждэг
RG 1 R1 1 R2
1 Rn
1/ n
1
12. Жишээ
$100,000-ын хөрөнгө оруулалт оны эцэст $50,000 болж
буурсан ба хоёр дахь жилийн эцэст эргээд $100,000
болсон:
X1 $100,000
X 2 $50,000
X 3 $100,000
Average rate of return:
(50%) (100%)
X
25%
2
Geometric rate of return:
RG 1 50% 1 100%
1/ 2
0.50 2
1/ 2
1
1 1 1 0%
1/ 2
13. Квартил
Эрэмбэлэгдсэн өгөгдлийг 4 тэнцүү хэсэгт хуваадаг
25%
25%
Q1
25%
Q2
i-р квартилийн байршил
25%
Q3
i n 1
Qi
4
Эрэмбэлэгдсэн өгөгдөл: 11 12 13 16 16 17 18 21 22
1 9 1
Position of Q1
2.5
4
Q1
12 13 12.5
2
Q1 ба Q3 нь төвийн хэмжигдэхүүн биш
Q2 = Медиан, төвийн хэмжигдэхүүн
14. 15. 16. 17. 18. Дисперс нь дараах төрлүүдтэй
Дисперсийн төрөл
Ерөнхий
Бүлгийн
Бүлэг хоорондын
Бүлгийн дундаж
Жинлэгдсэн
Жинлэгдээгүй
19. Стандарт хазайлт
Хэлбэлзлийн хамгийн чухал хэмжигдэхүүн
Дундажийн хэлбэлзлийг харуулдаг
Анхны өгөгдөлтэй ижил нэгжтэй байдаг
Түүврийн стандарт хазайлт:
n
S
X
i 1
i
X
2
n 1
Ерөнхий нийдмийн стандарт хазайлт:
N
X
i 1
i
N
2
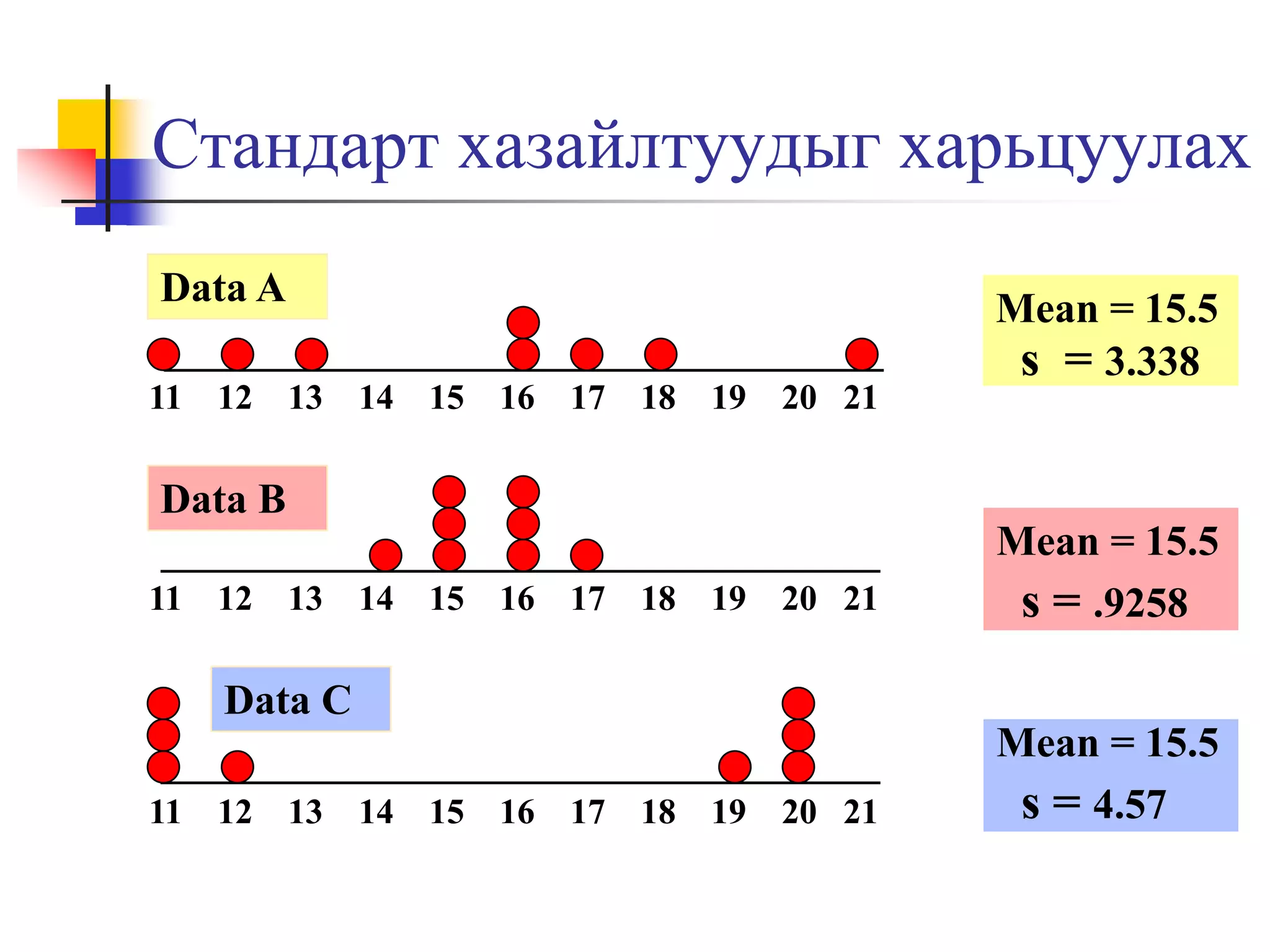
20. Стандарт хазайлтуудыг харьцуулах
Data A
11 12 13 14 15 16 17 18 19 20 21
Mean = 15.5
s = 3.338
Data B
11 12 13 14 15 16 17 18 19 20 21
Mean = 15.5
s = .9258
Data C
11 12 13 14 15 16 17 18 19 20 21
Mean = 15.5
s = 4.57
21. Вариацийн коэффициент
Хэлбэлзлийн харьцангуй хэмжигдэхүүн
Хувиар илэрхийлэгддэг (%)
Нэгж
дунджид
харуулдаг
харгалзах
хэлбэлзлийг
Ялгаатай нэгжээр хэмжигдсэн 2 ба түүнээс
дээш өгөгдлийг харьцуулахад ашиглагддаг
S
CV
X
100%
22. Вариацийн коэффициентийг
харьцуулах
Хувьцаа A:
Хувьцаа B:
Өмнөх жилийн дундаж үнэ = $50
Стандарт хазайлт = $5
Өмнөх жилийн дундаж үнэ = $100
Стандарт хазайлт = $5
Вариацийн коэфициент:
Хувьцаа A:
Хувьцаа B:
S
CV
X
$5
100%
100% 10%
$50
S
CV
X
$5
100%
100% 5%
$100
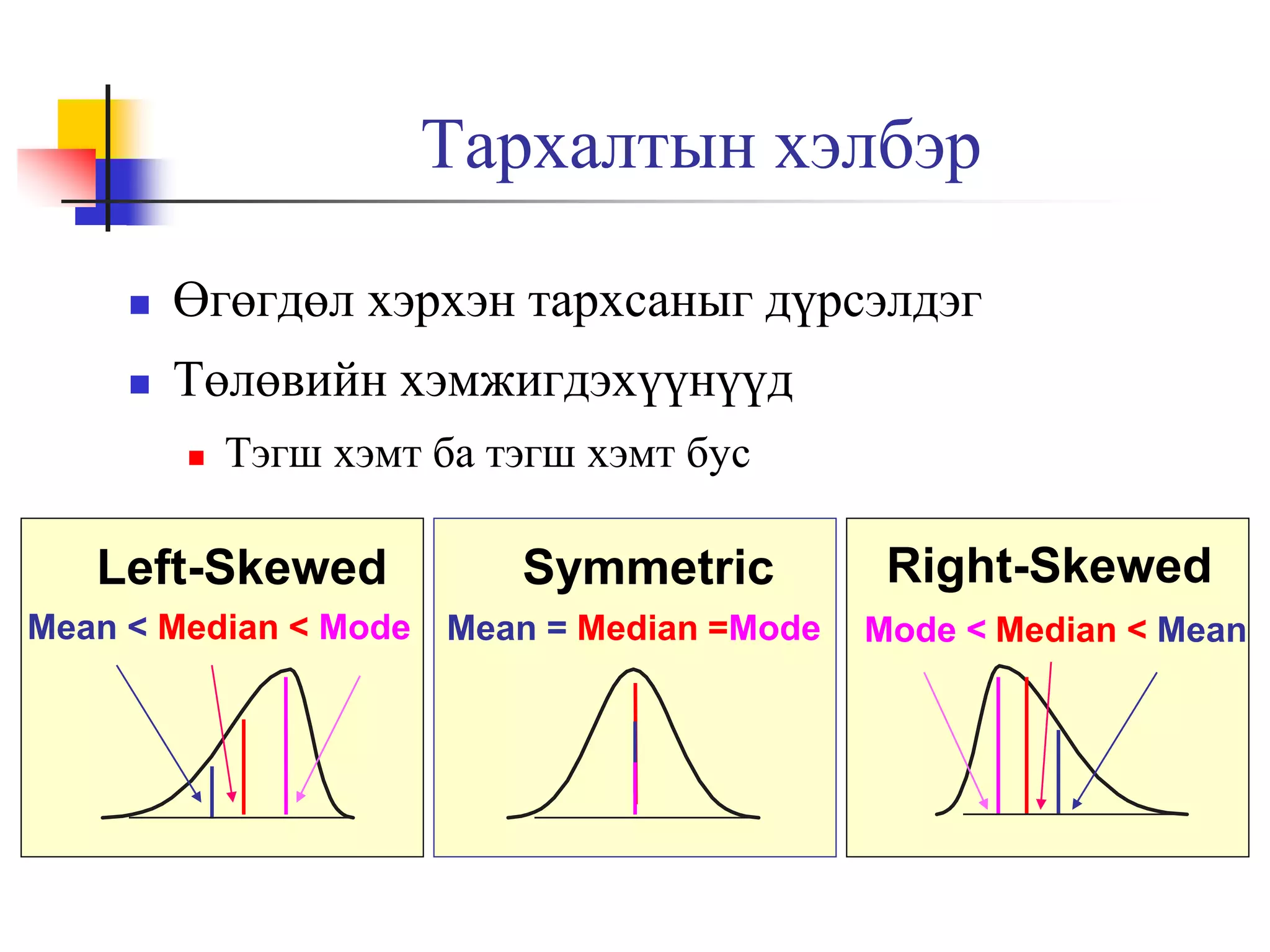
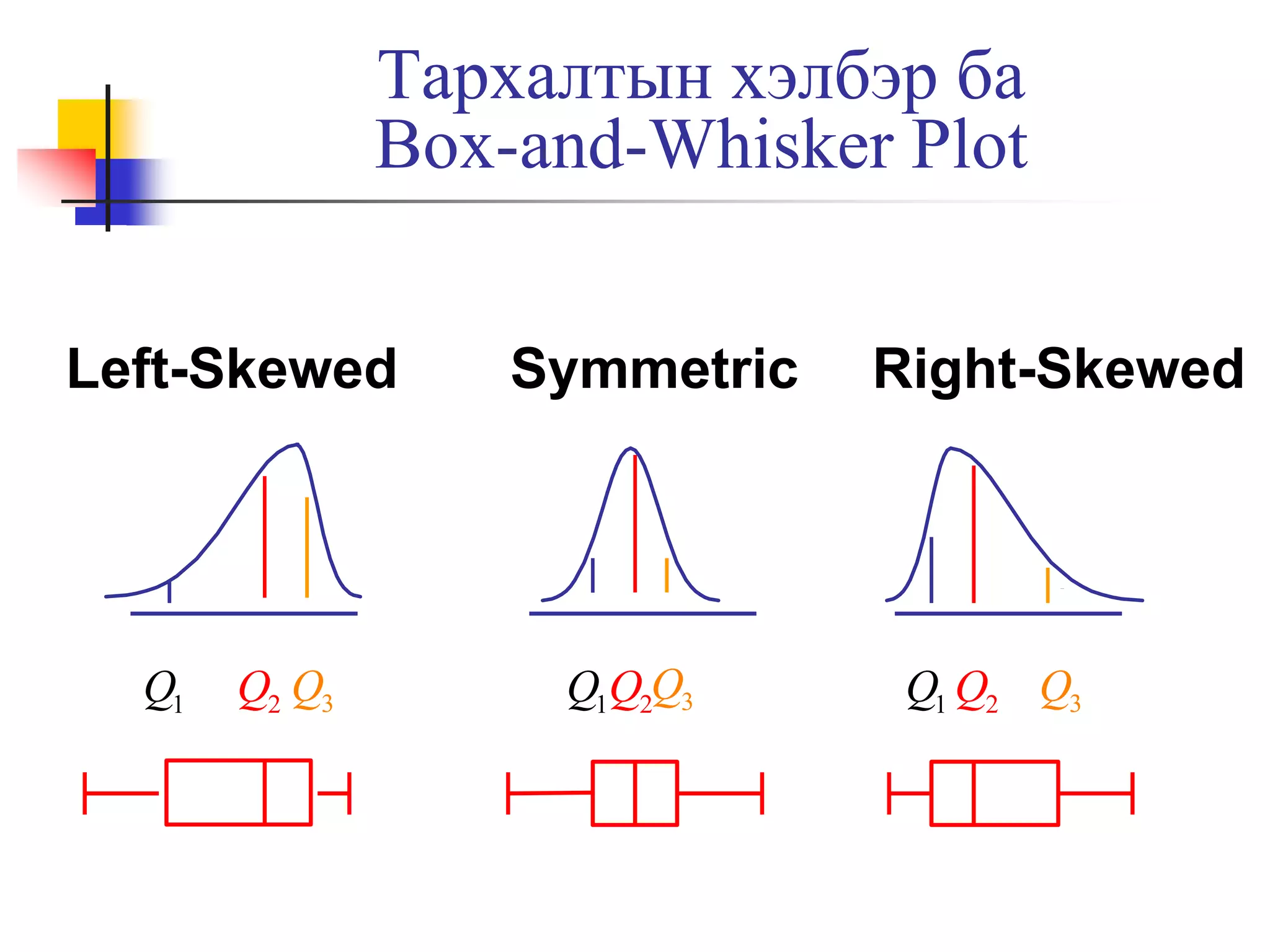
23. Тархалтын хэлбэр
Өгөгдөл хэрхэн тархсаныг дүрсэлдэг
Төлөвийн хэмжигдэхүүнүүд
Тэгш хэмт ба тэгш хэмт бус
Left-Skewed
Mean < Median < Mode
Symmetric
Mean = Median =Mode
Right-Skewed
Mode < Median < Mean
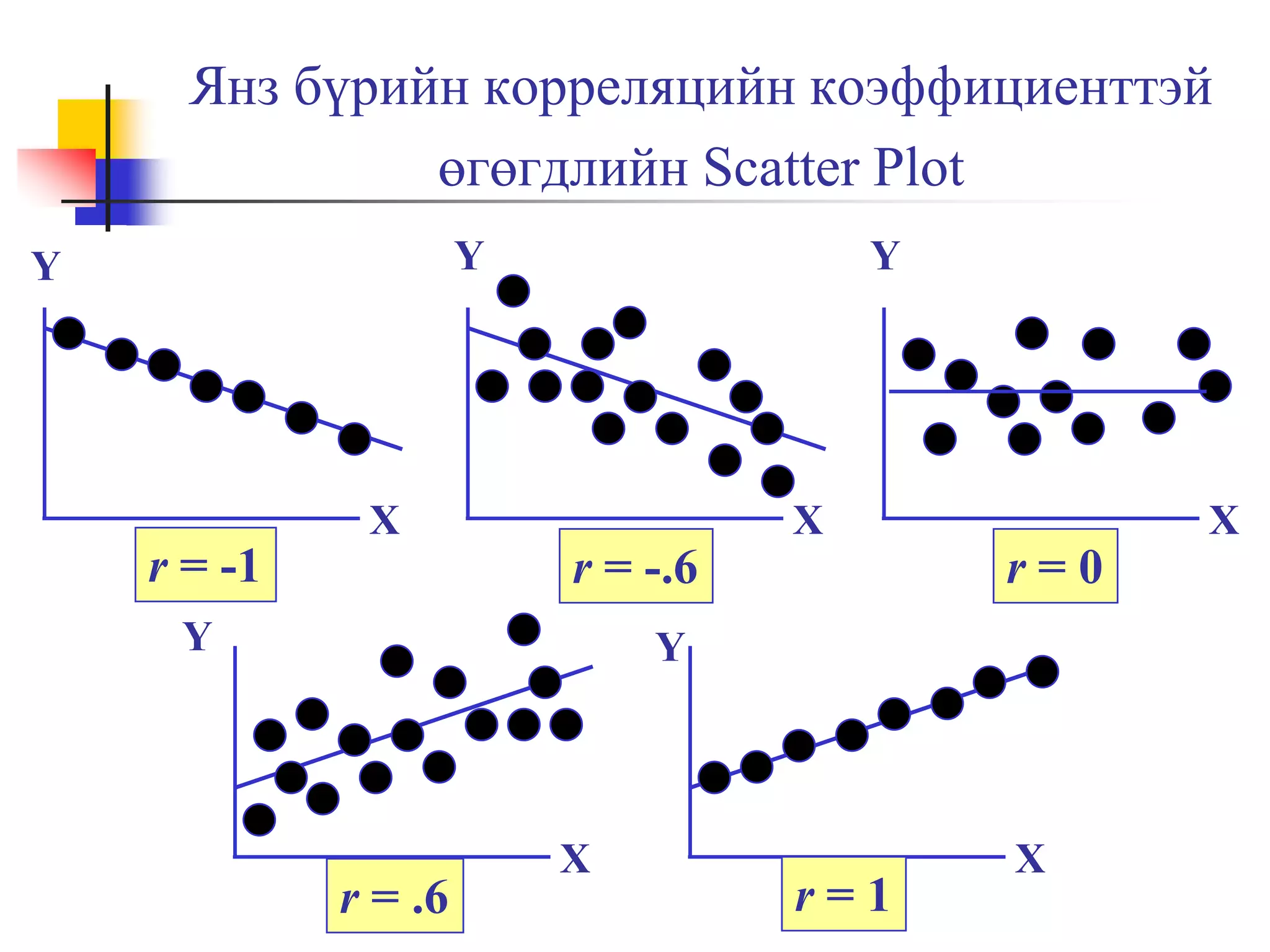
24. 25. 26. 27. Корреляцийн коэффициентийн
онцлог
–1 ба 1-ийн хооронд утга авна
–1-т ойр байвал хүчтэй сөрөг шугаман хамааралтай
1-т ойр байвал хүчтэй эерэг шугаман хамааралтай
0-т ойр байвал маш сул хамааралтай эсвэл ямар нэг
шугаман хамаарал байхгүй байна
28. 29. Тоон дескриптив
хэмжигдэхүүний занга
Өгөгдлийн шинжилгээ нь объектив
Өгөгдлийн
дэвшүүлэх
хэрэгтэй
тухай хамгийн сайн
тойм хэмжигдэхүүнийг
таамаглал
мэдээллэх
Өгөгдлийн тайлбар нь субъектив
Шударга, төвийг сахисан, тодорхой аргаар хийгдсэн
байх шаардлагатай
30. Шаардагдах нөхцөл
Тоон дискрептив хэмжигдэхүүн:
Баримт нь сайн ба муу үр дүнг аль алиныг нь
илэрхийлэх
Шударга, объектив ба төвийг сахисан байдлаар
илэрхийлэгдэх
Баримтыг гуйвуулах зохисгүй тойм
хэмжигдэхүүн ашиглахгүй байх
31. Сэдвийн дүгнэлт
Төвийн хэмжигдэхүүнийг дүрсэлсэн
Mean, median, mode, geometric mean, midrange
Квартилийн талаар хэлэлцсэн
Хэлбэлзлийн хэмжигдэхүүнийг дүрсэлсэн
Range, interquartile range, variance and standard
deviation, coefficient of variation
Тархалтын хэлбэрийг дүрсэлсэн
Symmetric, skewed, box-and-whisker plots
32.