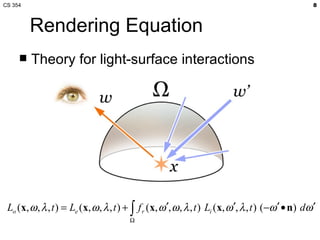
This document summarizes a class lecture on global illumination techniques for computer graphics. It discusses ray tracing and path tracing to solve the rendering equation through Monte Carlo integration. Radiosity for diffuse interreflection using form factors is covered. Participating media and photon mapping are also summarized. The next class will cover acceleration structures to speed up ray tracing computations. Project 4 is assigned, involving implementing a simple ray tracer.

1. CS 354
Global Illumination
Mark Kilgard
University of Texas
April 19, 2012

2. CS 354 2
Today’s material
 In-class quiz
 On ray casting & tracing lecture
 Lecture topic
 Project 4
 Global illumination

3. CS 354 3
My Office Hours
 Tuesday, before class
 Painter (PAI) 5.35
 8:45 a.m. to 9:15
 Thursday, after class
 ACE 6.302
 11:00 a.m. to 12
 Randy’s office hours
 Monday & Wednesday
 11 a.m. to 12:00
 Painter (PAI) 5.33

4. CS 354 4
Last time, this time
 Last lecture, we discussed
 Ray casting and tracing
 This lecture
 Global illumination
 Projects
 Project 3 due yesterday
 Project 4 on ray tracing on Piazza
 Due May 2, 2012

5. CS 354 5
On a sheet of paper
Daily Quiz • Write your EID, name, and date
• Write #1, #2, #3 followed by its answer
 Multiple choice: determining
if a ray intersects a sphere  Multiple choice: With
involves solving a distribution ray tracing, one can
accomplish
a) linear equation
a) depth-of-field
b) quadratic equation
b) soft shadows
c) system of linear equations
c) motion blur
d) cubic equation
d) a. and b. but not c.
 True or False: With ray
tracing, the problem of anti- e) a., b., and c.
aliasing doesn’t apply.

6. CS 354 6
Solving the Rendering Equation
with Ray Tracing
 Ray “tracing” or “shooting”
 Given a point and direction, sample radiance
 Building block for global illumination
algorithms
 Use ray traces to approximate integrals
 Conceptually, solving the rendering equation
 Intractable to shoot every ray
 Instead use Monte Carlo techniques

7. CS 354 7
Aspects of Modeling Light
 Geometric optics
 Our concern
 Assume light travels instantaneously
 Light travels in straight lines
 Light not influenced by gravity or magnetic fields
 Wave optics
 Diffraction, etc.
 Quantum optics
 Sub-microscopic

8. CS 354 8
Rendering Equation
 Theory for light-surface interactions
Lo (x, ω , λ , t ) = Le (x, ω , λ , t ) + ∫ f r (x, ω ′, ω , λ , t ) Li (x, ω ′, λ , t ) (−ω ′ • n) dω ′
Ω

9. CS 354 9
Rendering Equation Parts
Lo (x, ω , λ , t ) = Le (x, ω , λ , t ) + ∫ f r (x, ω ′, ω , λ , t ) Li (x, ω ′, λ , t ) (−ω ′ • n) dω ′
Ω
 Lo = outgoing light from x in direction ω
 x = point on a surface
 ω = normalized outgoing light vector
 λ = wavelength of light
 t = time
 Le = emitted light at x going towards from ω
 n = surface normal at x

10. CS 354 10
Rendering Equation Integral
 ∫ = integrate over a region
 Ω = region of a hemisphere
 Together: “integrate overall the incoming directions
for a hemisphere at a point x”
 ωˊ = normalized incoming light vector
 Li = incoming light at x coming from ωˊ
 n = surface normal at x
 (-ωˊ • n) = cosine of angle between incoming
light and surface normal
 dωˊ = differential of incoming angle

11. CS 354 11
Bidirectional Reflectance
Distribution Function
 Ratio of differential outgoing (reflected) radiance
to differential incoming irradiance
dLr (x, ω , λ , t ) dLr (x, ω , λ , t )
f r (x, ω ′, ω , λ , t ) = =
dEi (x, ω ′, λ , t ) dLi (x, ω ′, λ , t ) (−ω ′ • n) dω ′
 Physically based BRDF properties L = radiance
 Must be non-negative E = irradiance
 Must be reciprocal
 Swap incoming & relected directions generates same ratio
 Conserves energy
 Integrating over entire hemisphere must be ≤ 1

12. CS 354 12
Cosine Weighting for Irradiance
 At shallow angles, incoming light spreads over a
wider area of the surface
 Thus spreading the energy
 Thus dimming the received light

13. CS 354 13
Measuring BRDFs Empirically
 Gonioreflectometer is device to measure
BRDFs

14. CS 354 14
BRDF Decomposition
 Broad characterization of BRDF
appearance
Pure diffuse Pure specular Glossy

15. CS 354 15
Common BRDFs
 Diffuse model, a.k.a. Lambertian
f diffuse (x, Ψ ↔ Θ, λ , t ) = k d
( R • Θ) n
 Phongphong (x, Ψ ↔a.k.a.=Reflection dSpecular
f model, Θ, λ , t ) k s +k
N •Ψ
( N • H )n
f blinn (x, Ψ ↔ Θ, λ , t ) = k s + kd
 Blinn model, a.k.a. Half-angle Specular N •Ψ

16. CS 354 16
Hemisphere over a Surface
 Incident radiance is integrated over the
hemisphere

17. CS 354 17
Rendering Equation Interpretation
 Recursive equation
Lo (x, ω , λ , t ) = Le (x, ω , λ , t ) + ∫ f r (x, ω ′, ω , λ , t ) Li (x, ω ′, λ , t ) (−ω ′ • n) dω ′
Ω
outgoing light “sums up” all incoming light
for all directions on hemisphere
 Integral over hemisphere (Ω)
 Limitations
 Treats wavelengths all independent
 Treats time in Newtonian way
 Ignores volumetric and subsurface scattering
 More complex models can incorporate these aspects of light
 Impractical for actual computer graphics rendering

18. CS 354 18
Alternate Rendering Equation
 Integrate over all points in the scene
 Instead of all directions for a hemisphere
Lo (x, ω , λ , t ) = Le (x, ω , λ , t ) + ∫ f (x, ω
y∈Γ
r yx , ω , λ , t ) L(y, ωyx , λ , t ) G (x, y ) dy
outgoing light “sums up” all incoming light
for all surfaces, modulated by visibility
 Notes
 G(x,y) returns the visibility (occlusion) between points x & y
 Integral over all surface points (Γ) in the scene

19. CS 354 19
Two Versions of
Rendering Equation
Occlusion (G) is zero
o
Le (x, ω , λ , t ) +
Le (x, ω , λ , t ) +
Lo (x, ω , λ , t ) =
∫
Ω
f r (x, ω ′, ω , λ , t ) Li (x, ω ′, λ , t ) (−ω ′ • n) dω ′ Lo (x, ω , λ , t ) =
∫ f r (x, ωyx , ω , λ , t ) L(y, ωyx , λ , t ) G (x, y ) dy
y∈Γ
Integrate over hemisphere Integrate over all surface points

20. CS 354 20
Discrete Integral Approximation
 Uniform sampling
 Shown in 1D, but we need to integrate over
hemisphere (solid angles)

21. CS 354 21
Hemisphere Sampling
 Vary Euler angles

22. CS 354 22
Monte Carlo Integrations
 Randomly sample the rendering equation
integrals
 Sample space based on probability
distribution function
 Compute estimated variance to know when to
stop
 Importance sampling
 Try to weight probability function to match
variance

23. CS 354 23
Ray Casting for Initial Samples

24. CS 354 24
Path Tracing via
Simple Stochastic Ray Tracing

25. CS 354 25
Two Versions of
Rendering Equation (again) Occlusion (G) is zero
o
Le (x, ω , λ , t ) +
Le (x, ω , λ , t ) +
Lo (x, ω , λ , t ) =
∫
Ω
f r (x, ω ′, ω , λ , t ) Li (x, ω ′, λ , t ) (−ω ′ • n) dω ′ Lo (x, ω , λ , t ) =
∫ f r (x, ωyx , ω , λ , t ) L(y, ωyx , λ , t ) G (x, y ) dy
y∈Γ
Integrate over hemisphere Integrate over all surface points

26. CS 354 26
Sufficient Shadow Ray Sampling

27. CS 354 27
Light Tracing
 Trace rays from the light
 Contribution rays accumulate image samples

28. CS 354 28
Light Tracing Needs Lots of
Samples

29. CS 354 29
How many rays to shoot?
 Two approaches
 Fixed number of ray evaluations
 Limits the depth of recursion
 Means some paths can never be explored
 Implies bias in result, since favors short paths
 Russian Roulette approach
 Roll dice to see if ray tracing should continue
 Reduces bias in rendering result
 Allows “obscure” paths to be explored

30. CS 354 30
Radiosity History
 Used for thermal engineering since 1960s
 Introduced to computer graphics in 1984
 SIGGRAPH paper: “Modeling the Interaction
of Light Between Diffuse Surfaces”
 Goral, Torrance, Greenberg, Battaile (Cornell)
 Reduces to solving a linear system of
equations
 In simple formulation, just works for diffuse
surfaces
 OK for building interiors

31. CS 354 31
Radiosity Example

32. CS 354 32
Scene Diced into Uniform Patches

33. CS 354 33
Radiosity Method
Self-emitted reflectivity total
radiosity radiosity
Form factor
Approximation to general Rendering Equation

34. CS 354 34
Form Factors
 Form factor between i,j is Fij
 Tells how much of patch A is visible from patch B
 Indicates how much radiance can be transferred
1
Fij = ∫ ∫ K ( x, y ) dAy dAx
Ai Si Si
K ( x , y ) = G ( x, y ) V ( x, y )
cos(Θ xy , N x ) cos(−Θ xy , N y )
G ( x, y ) =
π rxy
2
V ( x, y ) =< visibility between x & y >

35. CS 354 35
Form Factor Visualized
 Mutual visibility of two patches
 Don’t have to be same size

36. CS 354 36
Differential Patches and
Foreshortening
 Cosine fall-off applies
 And assuming Lambertian surfaces
foreshortening

37. CS 354 37
Hemi-cube Approach to Sampling
Form Factors
 Think about drawing hemi-cube at every point
 What you see is an input for radiosity
 Known as “instant radiosity”

38. CS 354 38
Interpolation of Radiosity Solution
Constant Approximation “true” solution Quadratic Approximation
flat smooth

39. CS 354 39
Iterative Radiosity Solver
1 iteration 4 iterations 16 iterations
64 iterations 252 iterations

40. CS 354 40
Participating Media
 Light doesn’t just interact with surfaces
 Gaseous phenomena affects lighting
 Usually handled statistically
emission
in-scattering [Jarosz et.al. 2008]
absorption
out-scattering [FogShop 2007]

41. CS 354 41
Participating Media Assumptions
 Simpler
 Single scattering
 Uniform
 Ignore shadowing
 More complex
 Multiple scatterings
 Non-uniform
 Account for shadowing

42. CS 354 42
Photon Mapping
 Two-pass global illumination algorithm
 Developed by Henrick Jensen (1996)
 Two passes
 Randomly distribute photons around the scene
 Called “photon map construction”
 Render treating photons as mini-light sources
 Capable of efficiently generating otherwise very
expensive effects
 Caustics
 Diffuse inter-reflections, such as color bleed
 Sub-surface scattering

43. CS 354 43
Photon Mapping Examples
without diffuse photo map
caustics interreflection visualization
sub-surface scattering
diffuse interreflection

44. CS 354 44
Next Class
 Next lecture
 Acceleration structures
 How do we make the ray trace operation faster?
 Reading
 Chapter 5, 297-298
 Chapter 11, 569-577
 Project 4
 Project 4 is a simple ray tracer
 Due Wednesday, May 2, 2012