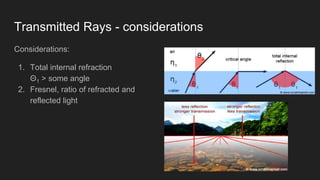
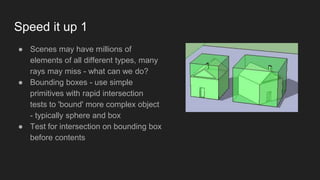
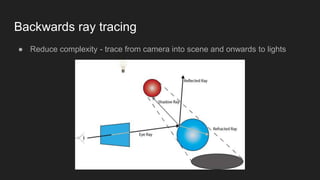
The document outlines the principles of ray tracing, a technique for simulating light and material interactions to create photorealistic images. It describes the algorithms involved, including tracing rays from the camera through the scene and calculating reflections, shadows, and illumination from various light sources. Additionally, it touches on material textures, anti-aliasing, and approaches for global illumination, highlighting methods to speed up the rendering process.

1. Ray Tracing
Fred's Friday Talk 19/10/2018

2. What is ray tracing?
● Simulating light and material interactions to produce photorealistic scenes
● This is not new, first algorithm was Arthur Appel (1968)
● Like AI it's time is coming (NVIDIA RTX ray tracing)

3. How do we ray trace?
● Traditional 3D renderers use rasterization, turning 3D models into polygons,
transform to 2D screen space and then shade pixels based on lights (REYES)
● Ray tracers simulate how lights rays interact with a 3D scene as happens with
photons and materials in the physical world
● Naive approach - as in the real works let's trace rays from lights through a
scene and materials to a camera
○ Tiny fraction of rays will reach camera
○ Computation requirements are beyond reach

4. Backwards ray tracing
● Reduce complexity - trace from camera into scene and onwards to lights

5. Basic algorithm
Raytrace() // top level function
for each pixel x,y
color(pixel) = Trace(ray_through_pixel(x,y))
Trace(ray) // fire a ray, return RGB radiance
object = closest_intersection(ray)
if object return Shade(object_point, ray)
else return Background_Color
Shade(point, ray) /* return radiance along ray */
radiance = black; /* initialize color vector */
for each light source
shadow_ray = calc_shadow_ray(point,light)
if !in_shadow(shadow_ray,light)
radiance += phong_illumination(point,ray,light)
radiance += spec_reflectance * Trace(reflected_ray(point,ray)))
radiance += spec_transmittance * Trace(refracted_ray(point,ray)))
return radiance

6. Shadow rays
● Simplest additional rays
● Send a ray to each light source
● If an object intersects, the object is in
shadow from this light source
● If we just do this, we will get intersections
with ourselves (floating point is inaccurate)
● Move start point for new ray trace just outside
of object and then trace ray

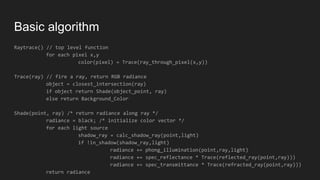
7. Object Intersections
● Basic geometry - sphere and some others here
● Ray is a vector R(t) = R0 + t.Rd (R0 origin, Rd direction)
● Sphere S set of points where (xs - xc)2 + (ys - yc)2 + (zs - zc)2 = Sr2
● Substituting: (X0 + Xd.t - Xc)2 + (Y0 + Yd.t - Yc)2 + (Z0 + Zd.t - Zc)2 = Sr2
● Quadratic of form At2 + Bt + C = 0 (if |Rd| = 1, A == 1) so
● A = 1, B = 2.(Xd.(X0 - Xc) + Yd.(Y0 - Yc) + Zd.(Z0 - Zc))}
C = (X0 - Xc)2 + (Y0 - Yc)2 + (Z0 - Zc)2 - Sr2
● Intersections t0, t1 = (- B ∓ (B2 - 4C)½) / 2
● If Discriminant < 0 (B2 - 4C) - no intersection, else t0 > 0 ? t0 : t1
● Point of intersection Ri = [xi, yi, zi] = [x0 + xd.ti , y0 + yd.ti, z0 +
zd.ti]
● Surface normal Sn = [(xi - xc)/Sr, (yi - yc)/Sr, (zi -

8. 1. Incident angle Θi = Angle of reflection Θr
2. I = A + B, R = A - B
3. B = cosΘ.N
4. I = A + cosΘ.N, R = A - cosΘ.N
5. A = I - cosΘ.N
6. R = I - cosΘ.N - cosΘ.N
7. R = I - 2.cosΘ.N
8. cosΘ = N⋅I
9. R = I - 2.(N⋅I).N
Reflected Rays

9. Transmitted Rays
Follows Snell's law - more steps, to summarize:
T = η.I + (ηc1 - c2).N
η = η1/η2 c1 = N⋅I, c2= (1-η2.(1-cos2Θ1))½
Need to consider whether you are leaving
or entering a material with higher η,
if so flip the surface normal N

10. Transmitted Rays - considerations
Considerations:
1. Total internal refraction
Θ1 > some angle
2. Fresnel, ratio of refracted and
reflected light

11. Local colour
3 main light types - Ambient, Diffuse and Specular

12. Ambient and Diffuse
● Ambient light is just a fixed value for the scene (background light)
● Diffuse is reflection from matt surfaces, where light is scattered evenly in all
directions - referred to as Lambertian Reflection
● Light per unit area is proportional to cosΘ = n⋅l
● For a single light: Ld = kd P max(0, n⋅l)
where
Ld diffuse reflected light
kd diffuse factor
P illumination from point light source

13. ● Lighting for glossy surfaces where light intensity
increases the closer viewer angle to the reflection vector
● cos(ɑ)n is a good approximation, n = specular coefficient
● To simplify vector calculation, it can be observed that the
half vector / near normal angle is always a good
approximation for ɑ
● h = bisector(v,l) and cos(ɑ) = n⋅h
● Ls = ks.P.max(o, n⋅h)n where
Ls specular reflected light
ks specular factor
n specular coefficient (shininess)
Specular reflection

14. Local colour formula

15. Summary
1. Send rays for every pixel
2. Find intersection with nearest object
3. Calculate shadow rays for all lights and how it affects contribution
4. Calculate local ambient, diffuse and specular contributions for each light
5. Calculate reflection vector and recurse, add contribution from ray
6. Calculate refraction vector and recurse, add contribution from ray
7. Shade pixel
● Attenuation along camera or light allows for fog or fading light sources
● Need to cap recursion - number of times or minimal contribution
● This is all great!

16. This isn't all great!
● What about materials and textures?
● All shadows are harsh
● We get anti-aliasing problems
● Our lens has infinite depth of field
● Illumination is local and not global
● At least it's quick now
😁

17. Materials and textures
● Basic material properties defined by R,G,B triple
for contribution by ambient, diffuse, specular,
reflected and refracted light
● How do we do wood, stone or bricks?
● Solution 1 - texture mapping (a lot more
geometry to map 2D images to a range of 3D
surface types) - think earth map on sphere
● Solution 2 - Procedural textures, algorithms to
simulate materials in 3D space
Read more

18. Materials and textures
● We can also model the bumpiness / texture of surfaces, not just their look
● We perturb the normal vector post intersection and prior to further calculations
● Solution 1 - displacement mapping, use 2D image, perturb based on image
● Solution 2 - procedurally determine the perturbation using an algorithm
● Matching visible and surface textures, leads to realistic surfaces

19. Distributed Ray Tracing
To solve a broad range of problems we can
use distributed ray tracing - distribute:
● through pixel - anti-aliasing
● in time - motion blur
● on reflection - better gloss model
● across light sources - penumbras
● across eye - depth of field
● across scene - diffuse interreflection

20. Global illumination
● Ray tracers generally consider local illumination, i.e. the colour contribution
form a small number of rays at a point
● The world is globally illuminated, all surfaces reflect light in all directions and
contribute colour to scenes

21. Global illumination
A number of approaches:
● Monte carlo ray tracing, a variant of
distributed ray tracing which on
intersection sends out 'random'
rays into the scene
● Radiosity - based on
thermodynamic heat transfer,
solves a massive linear equation
based on dividing scene into
patches and calculating transfer
between all patches

22. Speed it up 1
● Scenes may have millions of
elements of all different types, many
rays may miss - what can we do?
● Bounding boxes - use simple
primitives with rapid intersection
tests to 'bound' more complex object
- typically sphere and box
● Test for intersection on bounding box
before contents

23. Speed it up 2
● Use a variant of binary space
partitioning
● Octrees are common - subdivide
space as a series of cubes until you
get a certain number of objects
within a cube
● Use a standard line drawing
algorithm through the cubes until
you get to a cube with contents
● Ray trace as normal from this point

24. And more...
● One could go into detail or on for hours - but why not play with POV-RAY?