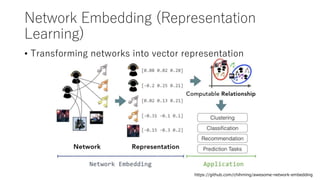
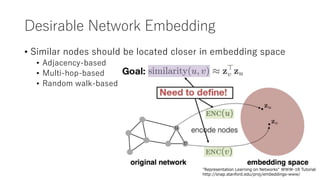
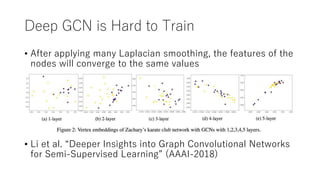
- Tsuyoshi Murata from the Tokyo Institute of Technology discusses using deep learning approaches for complex networks and graph neural networks. - He summarizes recent work on network embedding, including a paper on learning community structure with variational autoencoders and another on embedding multiplex networks. - Murata then discusses applications of graph neural networks, challenges in training deep GCNs, the representational power and limitations of GNNs, and open problems in the field like handling shallow structures, dynamic graphs, and scalability issues.

1. Tsuyoshi Murata
Tokyo Institute of Technology
murata@c.titech.ac.jp
www.net.c.titech.ac.jp
Deep Learning Approaches
for Networks

2. Complex Networks
• Community detection, graph partitioning, overlapping
communities,
• Local communities, community assessment and
benchmarking
• Effective algorithms for sorting nodes in large graphs,
finding patterns in graphs
• Visualization and exploration of large graphs
• Study and simulation of phenomena occurring on
networks
• Network evolution, link prediction, diffusion models
https://iutdijon.u-bourgogne.fr/marami/

3. Deep Neural Networks (DNNs)
Image recognition Voice recognition
Natural language
processing

4. Complex Networks + Deep Learning
• Neural networks as complex networks
• Deep compression [Han, ICLR 2016] : compressing neural networks
by pruning, quantization and Huffman coding
• Using neural networks for the tasks of complex networks
• Network Embedding
• Graph Neural Networks

5. Outline of This Talk
• Network Embedding
• Learning Community Structure with Variational Autoencoder (ICDM
2018)
• MELL: Effective Embedding Method for Multiplex Networks
(MATNet 2018)
• Graph Neural Networks
• Fast Approximations of Betweenness Centrality using Graph Neural
Networks (CIKM 2019)
• Linear Graph Convolutional Model for Diagnosing Brain Disorders
(Complex Networks 2019)

6. Network Embedding (Representation
Learning)
• Transforming networks into vector representation
https://github.com/chihming/awesome-network-embedding

7. "Representation Learning on Networks" WWW-18 Tutorial
http://snap.stanford.edu/proj/embeddings-www/
Desirable Network Embedding
• Similar nodes should be located closer in embedding space
• Adjacency-based
• Multi-hop-based
• Random walk-based

8. Challenges of Network Embedding
• Complex topological structure
• no spatial locality like grids
• methods for images do not work
• Defining similarity is not easy
• Combination of attributes and structure
• Several types of networks
• Signed networks (SIDE [Kim 2018], StEM [Rahaman 2018], SiNE [Wang
2018])
• Directed networks ([Perrault-joncas 2011], ATP [Sun 2018])
• Multilayer networks (MTNE [Xu 2017], MELL [Matsuno 2018])
• Temporal networks ([Singer 2019])
A Comprehensive Survey on Graph Neural Networks
https://arxiv.org/abs/1901.00596

9. Survey, Tutorial, Link
• A Survey on Network Embedding [Cui et al., 2017]
• https://arxiv.org/abs/1711.08752
• WWW-18 Tutorial : Representation Learning on Networks
• http://snap.stanford.edu/proj/embeddings-www/
• Awesome network embedding (links to papers and codes)
• https://github.com/chihming/awesome-network-embedding

10. Our Attempts for Network Embedding
• Learning Community Structure with Variational Autoencoder
(ICDM 2018)
• MELL: Effective Embedding Method for Multiplex Networks
(MATNet’18)

11. Learning Community Structure
with Variational Autoencoder
• Jun Jin Choong, Xin Liu, Tsuyoshi Murata (ICDM 2018)
• https://ieeexplore.ieee.org/document/8594831
• Variational autoencoder (VAE) : generative models for
classification and for generation of similar synthetic entities
• Variational graph autoencoder (VGAE) : the extension of VAE to
graph structures. Graph Convolutional Network is used for
encoder, and inner product is used for decoder
• Variational Graph Autoencoder for Community Detection
(VGAECD) : a new generative model which encodes graph
structures with multiple Gaussian distributions corresponding to
each of the communities

12. • Slides from Mr. Choong Jun Jin

13. MELL: Effective Embedding Method for
Multiplex Networks
• Ryuta Matsuno, Tsuyoshi Murata (MATNet’18)
• https://dl.acm.org/citation.cfm?id=3191565
• Introducing layer vectors as the similarity of layers
for better embedding

14. • Slides from Mr. Ryuta Matsuno

15. Outline of This Talk
• Network Embedding
• Learning Community Structure with Variational Autoencoder (ICDM
2018)
• MELL: Effective Embedding Method for Multiplex Networks
(MATNet 2018)
• Graph Neural Networks
• Fast Approximations of Betweenness Centrality using Graph Neural
Networks (CIKM 2019)
• Linear Graph Convolutional Model for Diagnosing Brain Disorders
(Complex Networks 2019)

16. What is Graph Neural Networks (GNN)?
• Generalization of NN models for graphs
• not so simple because graph data are irregular
• Two approaches for convolution
• Spectral-based convolution
• removing noise from graph signals
• relying on eigen-decomposition of graph Laplacian (O(N3) computation)
• Spatial-based convolution
• aggregating feature info from neighbors
• allowing edge features
A Comprehensive Survey on Graph Neural Networks
https://arxiv.org/abs/1901.00596
Graph Convolutional Networks
https://tkipf.github.io/graph-convolutional-networks/

17. Applications of Graph Neural Networks
• Computer vision
• scene graph generation (input : images, output: objects and semantic
relations)
• realistic image generation (input: scene graph, output: images)
• Recommender systems
• recommendation as link prediction (input: items & users, output: missing
links)
• Traffic
• Forecast of traffic speed (input: sensors on roads and the distances,
output: traffic speed and volume)
• Chemistry
• classification of molecular graphs (atoms = nodes, bonds = edges)
Graph Neural Networks: A Review of Methods and Applications
https://arxiv.org/abs/1812.08434

18. Deep GCN is Hard to Train
• After applying many Laplacian smoothing, the features of the
nodes will converge to the same values
• Li et al. “Deeper Insights into Graph Convolutional Networks
for Semi-Supervised Learning” (AAAI-2018)

19. Survey Papers of GNN
• “A Comprehensive Survey on Graph Neural Networks”
• Zonghan Wu, Shirui Pan, Fengwen Chen, Guodong Long, Chengqi Zhang,
Philip S. Yu
• https://arxiv.org/abs/1901.00596
• “Graph Neural Networks: A Review of Methods and Applications”
• Jie Zhou, Ganqu Cui, Zhengyan Zhang, Cheng Yang, Zhiyuan Liu, Lifeng
Wang, Changcheng Li, Maosong Sun
• https://arxiv.org/abs/1812.08434
• “Deep Learning on Graphs: A Survey”
• Ziwei Zhang, Peng Cui, Wenwu Zhu
• https://arxiv.org/abs/1812.04202

20. Links to GNN Resources
• Must-read papers on GNN
• https://github.com/thunlp/GNNPapers
• 9 survey papers
• 44 papers for models
• 102 papers for applications
• Awesome resources on Graph Neural Networks
• https://github.com/nnzhan/Awesome-Graph-Neural-
Networks

21. Towards Deep and Large GNNs
• “Cluster-GCN : An Efficient Algorithm for Training Deep and
Large Graph Convolutional Networks”, Wei-Lin Chiang,
Xuanqing Liu, Si Si, Yang Li, Samy Bengio, Cho-Jui Hsieh
[KDD 2019]
• https://arxiv.org/abs/1905.07953
• Neighborhood expansion is restricted within the clusters

22. Representation Properties and Limitations
of GNN
• “How Powerful Are Graph Neural Networks?”
• Keyulu Xu, Weihua Hu, Jure Leskovec, Stefanie Jegelka
• https://arxiv.org/abs/1810.00826
• GNNs are at most as powerful as WL (Weisfeiler-Lehman)
test in distinguishing graph structures
• Conditions on the neighborhood aggregation and graph
readout functions under which the resulting GNN is as
powerful as the WL test
Weisfeiler-Lehman Procedure
https://ethz.ch/content/dam/ethz/special-interest/bsse/borgwardt-
lab/documents/slides/CA10_WeisfeilerLehman.pdf

23. Computational Capacity Limits of GNN
• “What graph neural networks cannot learn: depth vs width”
• Andreas Loukas, 2019
• https://arxiv.org/abs/1907.03199
• What GNN can learn: GNN can compute any function that is
computable by a Turing machine if (i) there are enough layers,
(ii) layers have sufficient width, and two other conditions
(iii)(iv) (omitted) are satisfied
• What GNN cannot learn: GNN lose a significant portion of their
power when the product dw(depth x width) is limited Big Omega:
lower bound

24. Explainability of GNN
• GNN Explainer
• https://arxiv.org/pdf/1903.03894.pdf
• Show which feature of which node affects the prediction
• X for GCN
• http://openaccess.thecvf.com/content_CVPR_2019/papers/Pope_E
xplainability_Methods_for_Graph_Convolutional_Neural_Networks_C
VPR_2019_paper.pdf
• Show the importance of each node
• X for GN
• https://arxiv.org/pdf/1905.13686.pdf
• Show the importance of each node and each edge

25. Online Resources
• PyTorch Geometric (geometric deep learning extension
library for PyTorch)
• https://github.com/rusty1s/pytorch_geometric
• implements several GNNs (ChebNet, 1stChebNet, GraphSage,
MPNNs, GAT, SplineCNN)
• Deep Graph Library (DGL)
• https://www.dgl.ai/
• fast implementation of many GNNs
• Browse state-of-the-art in ML
• https://paperswithcode.com/task/graph-neural-network
• SOTA (the state of the art) algorithms of GNN and other tasks

26. Open Problems of GNNs
• shallow structures
• dynamic graphs
• non-structural scenarios
• scalability

27. Open Problems 1: Shallow Structure
• Traditional DNN can stack hundreds of layers to get better
performance (because deeper structure has more
parameters which improve the expressive power)
• GNN are always shallow, most of which are no more than
three layers
• Stacking multiple GCN layers will result in over-smoothing
(all vertices will converge to the same value)

28. Open problems 2: Dynamic Graphs
• Static graphs are stable so they can be modeled feasibly
• When edges and nodes appear and disappear, GNN cannot
change adaptively

29. Open Problems 3: Non-structural Scenarios
• There is no optimal methods to generate graphs from raw
data
• Finding the best graph generation approach will offer a wider
range of GNN application

30. Open Problems 4: Scalability
• How to apply embedding methods in Web-scale conditions
has been a fatal problem for almost all graph embedding
algorithms, and GNN is not an exception
• Scaling up GNN is difficult because many of the core steps
are computationally consuming in big data environment
• Graph data are not regular Euclidean, so batches cannot be applied
• Calculating graph Laplacian is also unfeasible when there are
millions of nodes and edges

31. Our Attempts for GNN
• Fast Approximations of Betweenness Centrality using Graph
Neural Networks (CIKM 2019)
• Linear Graph Convolutional Model for Diagnosing Brain
Disorders (Complex Networks 2019)

32. Fast Approximations of Betweenness
Centrality using Graph Neural Networks
• Sunil Kumar Maurya, Liu Xin, Tsuyoshi Murata (CIKM 2019)
• A novel GNN for approximating betweenness centrality
• aggregation is done separately for incoming and outgoing paths.
• Node’s own features are not aggregated. Each node gets unique
feature info corresponding to neighborhood structure
• Nodes with no shortest paths are identified and corresponding rows
in A and AT are set to zero

33. • Slides from Mr. Sunil Kumar Maurya

34. Linear Graph Convolutional Model for
Diagnosing Brain Disorders
• Zarina Rakhimberdina, Tsuyoshi Murata (Complex Networks
2019)

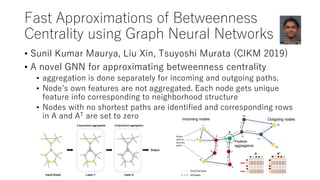
35. Semi-supervised learning on network using
structure features and graph convolution
[Tachibana et al., 2018]
• GCN uses local info only(such as 2-hop neighborhood info)
• Info about global structure is expected to improve the
performance
+
JSAI incentive award 2018
Semi-supervised learning on network using structure
features and graph convolution
https://jsai.ixsq.nii.ac.jp/ej/?action=pages_view_main&
active_action=repository_view_main_item_detail&item_i
d=9541&item_no=1&page_id=13&block_id=23

36. Complex Networks + Deep Learning :
Future Directions
• Explainable AI (XAI)
• Interpretable Machine Learning
• https://christophm.github.io/interpretable-ml-book/index.html
• Scene graph
• Interactions among objects can be easily modeled as a graph
• “LinkNet: Relational Embedding for Scene Graph” [NIPS 2018]
• Neural networks as complex networks
• Deep compression [Han, ICLR 2016]
• Deep learning systems as complex networks [Testolin, 2018]
• https://arxiv.org/abs/1809.10941

37. Acknowledgements
• Thank you for the organizers of MARAMI 2019
• Research funds
• JSPS Grant-in-Aid for Scientific Research (B)(Grant Number
17H01785)
• JST CREST (Grant Number JPMJCR1687)
• Many collaborators, especially Dr. Xin Liu (National
Institute of Advanced Industrial Science and Technology
(AIST), Japan)

38. Tsuyoshi Murata
Tokyo Institute of Technology
murata@c.titech.ac.jp
www.net.c.titech.ac.jp
Deep Learning Approaches for
Networks