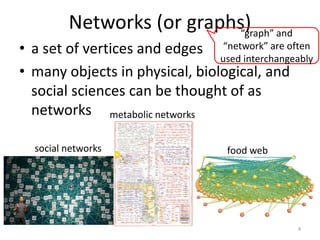
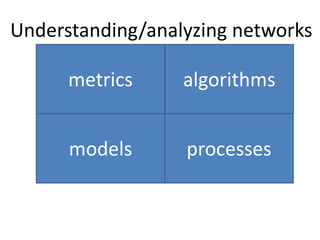
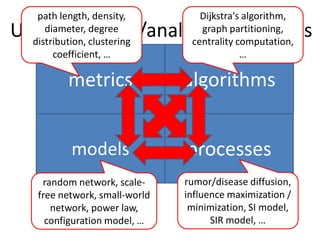
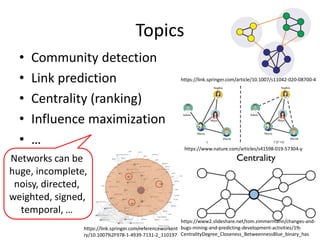
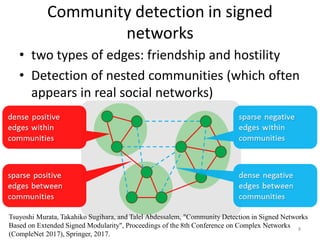
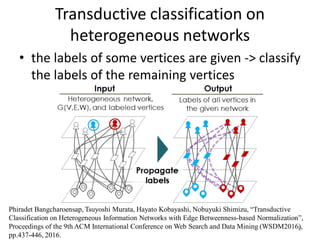
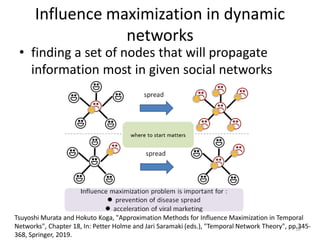
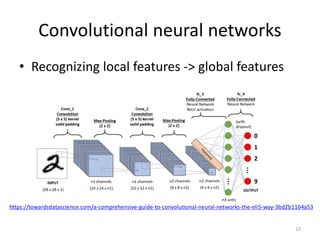
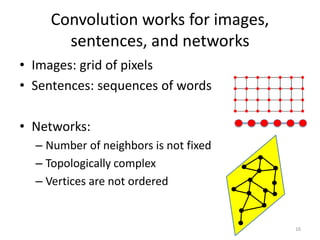
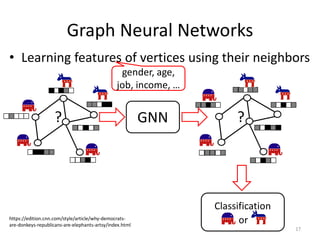
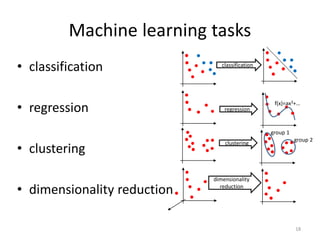
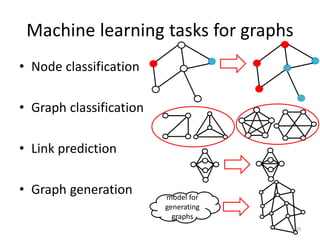
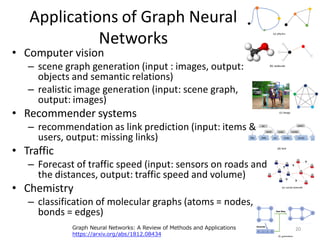
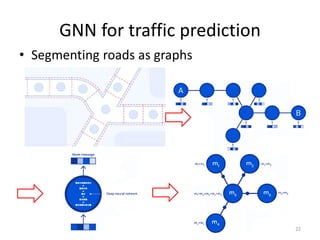
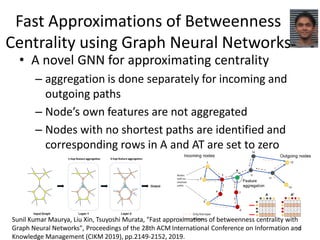
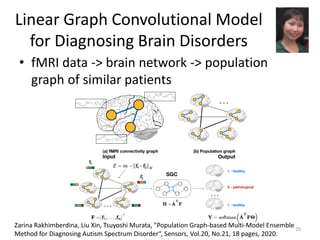
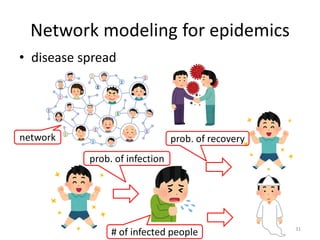
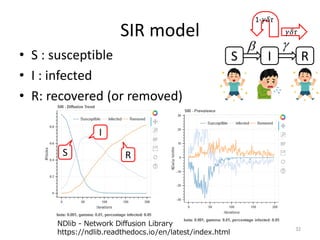
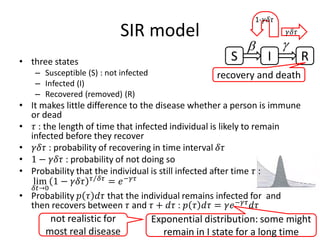
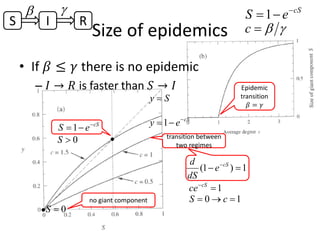
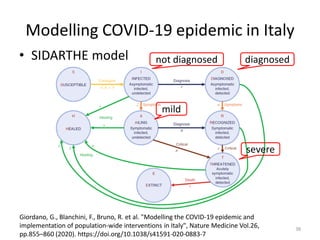
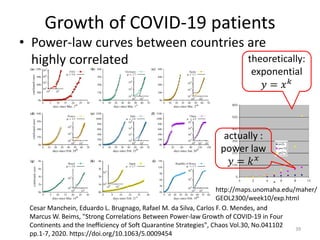
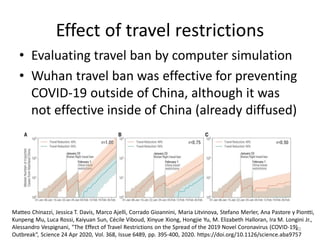
This document discusses networks and deep learning, with a focus on their application to analyzing the COVID-19 pandemic. It begins with an overview of networks and graph theory concepts. It then discusses how deep learning, specifically graph neural networks, can be used to analyze networks and learn representations of nodes. Applications discussed include traffic prediction and modeling disease spread. It also introduces the SIR model for modeling epidemics and the basic reproduction number metric.

1. Networks, Deep Learning
(and COVID-19)
Tsuyoshi Murata
Department of Computer Science
School of Computing
Tokyo Institute of Technology
murata@c.titech.ac.jp
http://www.net.c.titech.ac.jp/
The Tenth Workshop on Computation: Theory and Practice (WCTP 2020) Nov. 21(Sat) 2020

2. Table of contents
• Networks (graphs)
• Networks + Deep Learning
• Networks + Deep Learning + COVID-19
2

3. Table of contents
• Networks (graphs)
• Networks + Deep Learning
• Networks + Deep Learning + COVID-19
3

4. Networks (or graphs)
• a set of vertices and edges
• many objects in physical, biological, and
social sciences can be thought of as
networks
4
social networks
metabolic networks
food web
“graph” and
“network” are often
used interchangeably

5. Understanding/analyzing networks
metrics
models processes
algorithms

6. Understanding/analyzing networks
metrics
models processes
algorithms
path length, density,
diameter, degree
distribution, clustering
coefficient, …
Dijkstra's algorithm,
graph partitioning,
centrality computation,
…
random network, scale-
free network, small-world
network, power law,
configuration model, …
rumor/disease diffusion,
influence maximization /
minimization, SI model,
SIR model, …

7. Topics
• Community detection
• Link prediction
• Centrality (ranking)
• Influence maximization
• …
7
https://link.springer.com/article/10.1007/s11042-020-08700-4
https://www.nature.com/articles/s41598-019-57304-y
https://www2.slideshare.net/tom.zimmermann/changes-and-
bugs-mining-and-predicting-development-activities/19-
CentralityDegree_Closeness_BetweennessBlue_binary_has
https://link.springer.com/referenceworkent
ry/10.1007%2F978-1-4939-7131-2_110197
Networks can be
huge, incomplete,
noisy, directed,
weighted, signed,
temporal, …

8. Community detection in signed
networks
8
• two types of edges: friendship and hostility
• Detection of nested communities (which often
appears in real social networks)
Tsuyoshi Murata, Takahiko Sugihara, and Talel Abdessalem, "Community Detection in Signed Networks
Based on Extended Signed Modularity", Proceedings of the 8th Conference on Complex Networks
(CompleNet 2017), Springer, 2017.

9. Transductive classification on
heterogeneous networks
• the labels of some vertices are given -> classify
the labels of the remaining vertices
9
Phiradet Bangcharoensap, Tsuyoshi Murata, Hayato Kobayashi, Nobuyuki Shimizu, “Transductive
Classification on Heterogeneous Information Networks with Edge Betweenness-based Normalization”,
Proceedings of the 9th ACM International Conference on Web Search and Data Mining (WSDM2016),
pp.437-446, 2016.

10. Influence maximization in dynamic
networks
• finding a set of nodes that will propagate
information most in given social networks
10
Tsuyoshi Murata and Hokuto Koga, "Approximation Methods for Influence Maximization in Temporal
Networks", Chapter 18, In: Petter Holme and Jari Saramaki (eds.), "Temporal Network Theory", pp.345-
368, Springer, 2019.

11. Detecting Communities of Distant
Members
11
Xin Liu, Tsuyoshi Murata, Ken Wakita, "Detecting network communities beyond assortativity-related
attributes", Physical Review E 90, 012806, 2014.
Paulo Shakarian, Patrick Roos, Devon Callahan, Cory Kirk, "Mining for Geographically Disperse
Communities in Social Networks by Leveraging Distance Modularity", KDD2013.
• Our method was used for detecting terrorist
networks by the researchers of U.S. Military
Academy

12. Reference (Networks)
• Networks (second edition), Mark Newman,
Oxford University Press, 2018.
https://global.oup.com/academic/product/net
works-9780198805090

13. Table of contents
• Networks (graphs)
• Networks + Deep Learning
• Networks + Deep Learning + COVID-19
13

14. Deep Learning
Image recognition Voice recognition Natural Language
Processing
14

15. Convolutional neural networks
• Recognizing local features -> global features
https://towardsdatascience.com/a-comprehensive-guide-to-convolutional-neural-networks-the-eli5-way-3bd2b1164a53
15

16. Convolution works for images,
sentences, and networks
• Images: grid of pixels
• Sentences: sequences of words
• Networks:
– Number of neighbors is not fixed
– Topologically complex
– Vertices are not ordered
16

17. Graph Neural Networks
• Learning features of vertices using their neighbors
GNN
Classification
17
gender, age,
job, income, …
https://edition.cnn.com/style/article/why-democrats-
are-donkeys-republicans-are-elephants-artsy/index.html
? ?
or

18. Machine learning tasks
• classification
• regression
• clustering
• dimensionality reduction
regression
f(x)=ax3+…
clustering
group 1
group 2
dimensionality
reduction
classification
18

19. Machine learning tasks for graphs
• Node classification
• Graph classification
• Link prediction
• Graph generation model for
generating
graphs
19

20. Applications of Graph Neural
Networks
• Computer vision
– scene graph generation (input : images, output:
objects and semantic relations)
– realistic image generation (input: scene graph,
output: images)
• Recommender systems
– recommendation as link prediction (input: items &
users, output: missing links)
• Traffic
– Forecast of traffic speed (input: sensors on roads and
the distances, output: traffic speed and volume)
• Chemistry
– classification of molecular graphs (atoms = nodes,
bonds = edges)
Graph Neural Networks: A Review of Methods and Applications
https://arxiv.org/abs/1812.08434
20

21. DeepMind article (Sept. 2020)
• Traffic prediction with advanced Graph Neural
Networks
– https://deepmind.com/blog/article/traffic-
prediction-with-advanced-graph-neural-networks
21

22. GNN for traffic prediction
• Segmenting roads as graphs
22

23. Learning Community Structure
with Variational Autoencoder
• Variational autoencoder (VAE) : generative models for
the classification of similar synthetic entities
• Variational graph autoencoder (VGAE) : the extension
of VAE to graph structures
• Variational Graph Autoencoder for Community
Detection (VGAECD) : encodes graph structures with
multiple Gaussian distributions corresponding to each
of the communities
23
Jun Jin Choong, Xin Liu, Tsuyoshi Murata, "Learning Community Structure with Variational Autoencoder",
Proceedings of IEEE ICDM 2018 (IEEE International Conference on Data Mining), pp.69-78, November, 2018.

24. Fast Approximations of Betweenness
Centrality using Graph Neural Networks
• A novel GNN for approximating centrality
– aggregation is done separately for incoming and
outgoing paths
– Node’s own features are not aggregated
– Nodes with no shortest paths are identified and
corresponding rows in A and AT are set to zero
24
Sunil Kumar Maurya, Liu Xin, Tsuyoshi Murata, "Fast approximations of betweenness centrality with
Graph Neural Networks", Proceedings of the 28th ACM International Conference on Information and
Knowledge Management (CIKM 2019), pp.2149-2152, 2019.

25. Linear Graph Convolutional Model
for Diagnosing Brain Disorders
25
• fMRI data -> brain network -> population
graph of similar patients
Zarina Rakhimberdina, Liu Xin, Tsuyoshi Murata, "Population Graph-based Multi-Model Ensemble
Method for Diagnosing Autism Spectrum Disorder“, Sensors, Vol.20, No.21, 18 pages, 2020.

26. Reference (Graph Neural Networks)
• “Graph Neural Networks: Models and
Applications” (tutorial of AAAI 2020)
• https://cse.msu.edu/~mayao4/tutorials/aaai2
020/
26

27. Table of contents
• Networks (graphs)
• Networks + Deep Learning
• Networks + Deep Learning + COVID-19
27

28. Table of contents
• Networks (graphs)
• Networks + Deep Learning
• Networks + Deep Learning + COVID-19
– Networks + COVID-19
– Networks + Deep Learning + COVID-19
28

29. Table of contents
• Networks (graphs)
• Networks + Deep Learning
• Networks + Deep Learning + COVID-19
– Networks + COVID-19
– Networks + Deep Learning + COVID-19
29

30. Network modeling for epidemics
• disease spread
30

31. Network modeling for epidemics
• disease spread
31
network
# of infected people
prob. of infection
prob. of recovery

32. SIR model
• S : susceptible
• I : infected
• R: recovered (or removed)
32
S I R
β γ
𝛾𝛾𝛾𝛾𝛾𝛾
1-𝛾𝛾𝛾𝛾𝛾𝛾
S
I
R
NDlib - Network Diffusion Library
https://ndlib.readthedocs.io/en/latest/index.html

33. SIR model
• three states
– Susceptible (S) : not infected
– Infected (I)
– Recovered (removed) (R)
• It makes little difference to the disease whether a person is immune
or dead
• 𝜏𝜏 : the length of time that infected individual is likely to remain
infected before they recover
• 𝛾𝛾𝛾𝛾𝜏𝜏 : probability of recovering in time interval 𝛿𝛿𝛿𝛿
• 1 − 𝛾𝛾𝛾𝛾𝛾𝛾 : probability of not doing so
• Probability that the individual is still infected after time 𝜏𝜏 :
lim
𝛿𝛿𝑡𝑡→0
1 − 𝛾𝛾𝛾𝛾𝛾𝛾 ⁄𝜏𝜏 𝛿𝛿𝛿𝛿
= 𝑒𝑒−𝛾𝛾𝛾𝛾
• Probability 𝑝𝑝 𝜏𝜏 𝑑𝑑𝜏𝜏 that the individual remains infected for and
then recovers between 𝜏𝜏 and 𝜏𝜏 + 𝑑𝑑𝜏𝜏 : 𝑝𝑝 𝜏𝜏 𝑑𝑑𝜏𝜏 = 𝛾𝛾𝑒𝑒−𝛾𝛾𝛾𝛾
𝑑𝑑𝜏𝜏
S I R
recovery and death
β γ
𝛾𝛾𝛾𝛾𝛾𝛾
1-𝛾𝛾𝛾𝛾𝛾𝛾
Exponential distribution: some might
remain in I state for a long time
not realistic for
most real disease

34. Equations for the SIR model
•
𝑑𝑑𝑑𝑑
𝑑𝑑𝑑𝑑
= −𝛽𝛽𝑠𝑠𝑠𝑠
•
𝑑𝑑𝑑𝑑
𝑑𝑑𝑑𝑑
= 𝛽𝛽𝑠𝑠𝑠𝑠 − 𝛾𝛾𝑥𝑥
•
𝑑𝑑𝑟𝑟
𝑑𝑑𝑑𝑑
= 𝛾𝛾𝑥𝑥
• 𝑠𝑠 + 𝑥𝑥 + 𝑟𝑟 = 1
• Eliminate x :
1
𝑠𝑠
𝑑𝑑𝑑𝑑
𝑑𝑑𝑑𝑑
= −
𝛽𝛽
𝛾𝛾
𝑑𝑑𝑑𝑑
𝑑𝑑𝑑𝑑
• Integrate both sides with respect to t : 𝑠𝑠 = 𝑠𝑠0 𝑒𝑒 ⁄−𝛽𝛽𝑟𝑟 𝛾𝛾
• Put this equation and x = 1 − 𝑠𝑠 − 𝑟𝑟 :
𝑑𝑑𝑑𝑑
𝑑𝑑𝑑𝑑
= 𝛾𝛾�
�
1 − 𝑟𝑟 −
𝑠𝑠0 𝑒𝑒 ⁄−𝛽𝛽𝑟𝑟 𝛾𝛾
• 𝑡𝑡 =
1
𝛾𝛾
∫0
𝑟𝑟 𝑑𝑑𝑑𝑑
1−𝑟𝑟−𝑠𝑠0 𝑒𝑒 ⁄−𝛽𝛽𝑟𝑟 𝛾𝛾
S I R
𝑠𝑠
β γ
𝑥𝑥 𝑟𝑟
S
R
I
Time evolution of the SIR model
𝛽𝛽 = 1, 𝛾𝛾 = 0.4, 𝑠𝑠0 = 0.99, 𝑥𝑥0 =
0.01, 𝑟𝑟0 = 0

35. Time evolution of the SIR model
• S decreases / R increases monotonically
• S does not go to zero (because no I left as 𝑡𝑡 → ∞)
• R: total size of the outbreak
•
𝑑𝑑𝑑𝑑
𝑑𝑑𝑑𝑑
= 𝛾𝛾 1 − 𝑟𝑟 − 𝑠𝑠0 𝑒𝑒 ⁄−𝛽𝛽𝑟𝑟 𝛾𝛾
= 0
• 𝑟𝑟 = 1 − 𝑠𝑠0 𝑒𝑒 ⁄−𝛽𝛽𝑟𝑟 𝛾𝛾
• Initial condition:
– c infected and n-c susceptible
– 𝑠𝑠0 = 1 − ⁄𝑐𝑐 𝑛𝑛 , 𝑥𝑥0 = ⁄𝑐𝑐 𝑛𝑛 , 𝑟𝑟0 = 0
– When 𝑛𝑛 → ∞, 𝑠𝑠0 ≅ 1
• 𝑟𝑟 = 1 − 𝑒𝑒 ⁄−𝛽𝛽𝑟𝑟 𝛾𝛾
S
R
I
Time evolution of the SIR model
𝛽𝛽 = 1, 𝛾𝛾 = 0.4, 𝑠𝑠0 = 0.99, 𝑥𝑥0 =
0.01, 𝑟𝑟0 = 0
Size of the giant component
of a Poisson random graph
𝑐𝑐 = ⁄𝛽𝛽 𝛾𝛾
cS
eS −
−=1
size

36. Size of epidemics
• If 𝛽𝛽 ≤ 𝛾𝛾 there is no epidemic
– 𝐼𝐼 → 𝑅𝑅 is faster than 𝑆𝑆 → 𝐼𝐼
Sy =
cS
ey −
−=1cS
eS −
−=1
no giant component
0=S
0>S transition between
two regimes
1)1( =− −cS
e
dS
d
1=−cS
ce
10 =→= cS
cS
eS −
−=1
γβ=c
S I R
β γ
Epidemic
transition
𝛽𝛽 = 𝛾𝛾

37. Basic reproduction number
• The average number of additional I people
– If each I person passes disease to two others on
average, then 𝑅𝑅0 = 2 → disease will grow
exponentially
– If 𝑅𝑅0 = ⁄1 2 → disease will die exponentially
– If 𝑅𝑅0 = 1 → epidemic threshold (𝛽𝛽 = 𝛾𝛾)
S I R
𝑠𝑠
β γ
𝑥𝑥 𝑟𝑟

38. Modelling COVID-19 epidemic in Italy
• SIDARTHE model
38
Giordano, G., Blanchini, F., Bruno, R. et al. "Modelling the COVID-19 epidemic and
implementation of population-wide interventions in Italy", Nature Medicine Vol.26,
pp.855–860 (2020). https://doi.org/10.1038/s41591-020-0883-7
diagnosednot diagnosed
severe
mild

39. Growth of COVID-19 patients
• Power-law curves between countries are
highly correlated
39
Cesar Manchein, Eduardo L. Brugnago, Rafael M. da Silva, Carlos F. O. Mendes, and
Marcus W. Beims, "Strong Correlations Between Power-law Growth of COVID-19 in Four
Continents and the Inefficiency of Soft Quarantine Strategies", Chaos Vol.30, No.041102
pp.1-7, 2020. https://doi.org/10.1063/5.0009454
theoretically:
exponential
𝑦𝑦 = 𝑥𝑥 𝑘𝑘
http://maps.unomaha.edu/maher/
GEOL2300/week10/exp.html
actually :
power law
𝑦𝑦 = 𝑘𝑘 𝑥𝑥

40. Effect of travel restrictions
• Evaluating travel ban by computer simulation
• Wuhan travel ban was effective for preventing
COVID-19 outside of China, although it was
not effective inside of China (already diffused)
40
Matteo Chinazzi, Jessica T. Davis, Marco Ajelli, Corrado Gioannini, Maria Litvinova, Stefano Merler, Ana Pastore y Piontti,
Kunpeng Mu, Luca Rossi, Kaiyuan Sun, Cécile Viboud, Xinyue Xiong, Hongjie Yu, M. Elizabeth Halloran, Ira M. Longini Jr.,
Alessandro Vespignani, "The Effect of Travel Restrictions on the Spread of the 2019 Novel Coronavirus (COVID-19)
Outbreak“, Science 24 Apr 2020, Vol. 368, Issue 6489, pp. 395-400, 2020. https://doi.org/10.1126/science.aba9757

41. Network analysis of genomes
41
Peter Forstera, Lucy Forster, Colin Renfrew, and Michael Forster, "Phylogenetic Network
Analysis of SARS-CoV-2 Genomes“, PNAS, Vol.117, No.17, pp.9241-9243, 2020
https://doi.org/10.1073/pnas.2004999117
A
BC
Bat
Europe and America
East Asia
• Phylogenetics: for the inference of the
evolutionary history and relationships among
groups of organisms
• Three variants
• Virus mutation emerges
in two different hosts

42. Table of contents
• Networks (graphs)
• Networks + Deep Learning
• Networks + Deep Learning + COVID-19
– Networks + COVID-19
– Networks + Deep Learning + COVID-19
42

43. Graph Representation Learning and
Beyond (GRL+)
• A workshop collocated with
International Conference on Machine
Learning (ICML 2020)
– https://grlplus.github.io/covid19/
• “Graph Methods for COVID-19
Response” William L. Hamilton
(McGill University/Mila)
– https://grlplus.github.io/files/graphs-
against-covid.pdf
43

44. “Graph Methods for COVID-19
Response”
• Three key types of data
– Biomedical treatment data
– Epidemiological network data
– Supply chain networks
• heterogeneous and relational structures
– Computational drug design
– Computational treatment design
– Epidemiological forecasting
– Demand forecasting and supply chain optimization
– Outbreak tracking and tracing
44
William L. Hamilton, "Graph Methods for COVID-19 Response", https://grlplus.github.io/files/graphs-
against-covid.pdf

45. Computational drug design
• Can we design better antivirals to target COVID-19?
• Sub-problem 1: Molecule representation and
property prediction
• Sub-problem 2: Molecule generation and search
– How can we generate molecules that have particular
properties? How can we effectively search over the
space of possible molecules?
45
possibility of application of
GNNs (still open challenge)
William L. Hamilton, "Graph Methods for COVID-19 Response", https://grlplus.github.io/files/graphs-
against-covid.pdf

46. Computational treatment design
• Can we design better treatment strategies
using existing drugs?
• Approach 1: structure-based
– similar to computational drug design
• Approach 2: network-based
– Leverage knowledge of biological interactions
between drugs, diseases, and proteins
46
William L. Hamilton, "Graph Methods for COVID-19 Response", https://grlplus.github.io/files/graphs-
against-covid.pdf

47. Epidemiological forecasting
• Can we better predict how and where
infection rate will change over time?
47
William L. Hamilton, "Graph Methods for COVID-19 Response", https://grlplus.github.io/files/graphs-
against-covid.pdf

48. Demand forecasting and supply chain
optimization
• Can we forecast COVID-19 related demands to
optimize supply chains?
1. Heterogeneous relational data
2. Temporal information and changes
3. Node-level predictions
-> spatio-temporal GNNs are useful
48
William L. Hamilton, "Graph Methods for COVID-19 Response", https://grlplus.github.io/files/graphs-
against-covid.pdf

49. Outbreak tracking and tracing
• Can we model and predict infection risk at the
individual level?
49
William L. Hamilton, "Graph Methods for COVID-19 Response", https://grlplus.github.io/files/graphs-
against-covid.pdf

50. “COVID-19 and Networks”
• an article in Journal of the Japanese Society
for Artificial Intelligence (written in Japanese)
Tsuyoshi Murata, “COVID-19 and
Networks”, Journal of JSAI, Vol.35,
No.5, pp.654-660, 2020
http://id.nii.ac.jp/1004/00010709/
50

51. Table of contents
• Networks (graphs)
• Networks + Deep Learning
• Networks + Deep Learning + COVID-19
51

52. Networks, Deep Learning
(and COVID-19)
Tsuyoshi Murata
Department of Computer Science
School of Computing
Tokyo Institute of Technology
murata@c.titech.ac.jp
http://www.net.c.titech.ac.jp/
The Tenth Workshop on Computation: Theory and Practice (WCTP 2020) Nov. 21(Sat) 2020
slides available
from here