Download as PDF, PPTX
![実行
• {rstan}で実行しました.
• 割愛しますがソースコード等は以下の記事になります.
• [Stan]「使える大学・使えない大学」の事例から考えるアンケートの解析方法
• http://heartruptcy.blog.fc2.com/blog-entry-162.html](https://image.slidesharecdn.com/20150221-150221021751-conversion-gate01/85/slide-30-320.jpg)
More Related Content
順序データでもベイズモデリング
- 1.
- 2.
- 3.
- 4. 再現性 いつどこで誰がやっても同じ結果になるか • バージョン管理, ドキュメンテーション •Git, {knitr} 頑健性 データやモデルを少しだけ変えても同じような結果になるか • 頑健な手法 • 検定: wilcox.test() • 相関: {minerva} mine() • 回帰: {MASS} rlm(), {quantreg} rg(), loess() • クラスタリング: {e1071} bclust()
- 5. 幅を見る • （パラメータの）信頼区間 • （新しいデータの）予測区間 •ブートストラップ • クロスバリデーション
- 6. 幅を見る • （パラメータの）信頼区間 • （新しいデータの）予測区間 •ブートストラップ • クロスバリデーション Take a Risk：林岳彦の研究メモ おっと危ない：信頼区間と予測区間を混同しちゃダメ http://takehiko-i-hayashi.hatenablog.com/entry/20110204/1296773267 参考: takehiko-i-hayashi さんの記事
- 7. おすすめはベイズモデリング • 十分に広い一様な事前分布𝑝 𝜃をとれば、 事後分布 𝑝 𝜃|𝑋 ∝ 𝑝 𝜃 𝑝 𝑋|𝜃 を最大にする𝜃 = 𝜃∗は最尤推定量と一致する。 • しかし、最尤推定量𝜃∗を使った予測分布𝑓 𝑥 = 𝑝 𝑥|𝜃∗ と、 ベイズ推定による予測分布 𝑓 𝑥 = 𝑝 𝑥|𝜃 𝑝 𝜃|𝑋 𝑑𝜃 は モデルが複雑になると一致しない。 𝜃の幅（分布）が効いてくる！ • 最尤推定量を使った予測分布は過適合になりやすい。 事前分布を決めないとダメ なんでも幅をつけられる 複雑な確率モデルでも大丈夫
- 8. ベイズモデリング可能なRパッケージ • {bayesm} • {MCMCpack} •{Zelig} • SAS MCMC proc • {R2WinBUGS} • {rjags},{runjags} • {rstan} • {LaplacesDemon} 息してない？ 約40個のモデルから選ぶのが面倒 ラク・結構速い ちょっと遅い サンプラーが豊富 1行で 実行 モデル式 書くよ 離散パラメータ使いづらい 収束しやすい エラーメッセージが地獄 使いやすい
- 9. ｛Zelig｝の紹介 • Rの色々な解析手法の統合ラッパーを目指す • ベイズモデリングの部分は今のところ{MCMCpack}のラッパー •階層ベイズや時系列モデルも予定に入っている
- 10. ベイズモデルな過去の発表 @berobero11@yokkunsさん @siero5335さん @sanoche16さんが 2/28(土)にTokyoWebminigで 「ベイジアンモデリングによるマーケティングサイエンス」発表予定！
- 11.
- 12.
- 13.
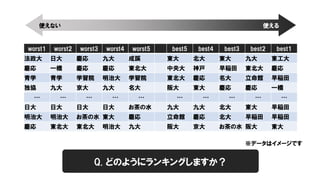
- 14. worst1 worst2 worst3worst4 worst5 best5 best4 best3 best2 best1 法政大 日大 慶応 九大 成蹊 東大 北大 東大 九大 東工大 慶応 一橋 慶応 慶応 東北大 中央大 神戸 早稲田 東北大 慶応 青学 青学 学習院 明治大 学習院 東北大 慶応 名大 立命館 早稲田 独協 九大 京大 九大 名大 阪大 東大 慶応 慶応 一橋 … … … … … … … … … … 日大 日大 日大 日大 お茶の水 九大 九大 北大 東大 早稲田 明治大 明治大 お茶の水 東大 慶応 立命館 慶応 北大 早稲田 早稲田 慶応 東北大 東北大 明治大 九大 阪大 京大 お茶の水 阪大 東大 使えない 使える ※データはイメージです Q. どのようにランキングしますか？
- 15. worst1 worst2 worst3worst4 worst5 best5 best4 best3 best2 best1 法政大 日大 慶応 九大 成蹊 東大 北大 東大 九大 東工大 慶応 一橋 慶応 慶応 東北大 中央大 神戸 早稲田 東北大 慶応 青学 青学 学習院 明治大 学習院 東北大 慶応 名大 立命館 早稲田 独協 九大 京大 九大 名大 阪大 東大 慶応 慶応 一橋 ・・・ ・・・ ・・・ ・・・ ・・・ ・・・ ・・・ ・・・ ・・・ ・・・ 日大 日大 日大 日大 お茶の水 九大 九大 北大 東大 早稲田 明治大 明治大 お茶の水 東大 慶応 立命館 慶応 北大 早稲田 早稲田 慶応 東北大 東北大 明治大 九大 阪大 京大 お茶の水 阪大 東大 1点 2点 3点 4点 5点5点 4点 3点 2点 1点 「使えるポイント・使えないポイント」の集計
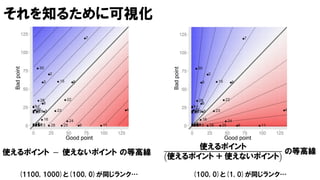
- 16. ネット上の議論 使えるポイント − 使えないポイントでソートすべき 使えるポイント 使えるポイント ＋ 使えないポイント でソートすべき 僕個人の意見 可視化としては上記のようなオレオレ指標をどんどん使ってOK でもそれはトドメの解析や意思決定では使わない方がよい
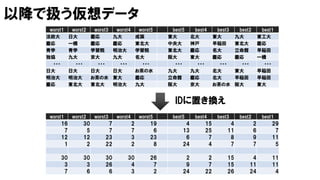
- 17. 以降で扱う仮想データ worst1 worst2 worst3worst4 worst5 best5 best4 best3 best2 best1 法政大 日大 慶応 九大 成蹊 東大 北大 東大 九大 東工大 慶応 一橋 慶応 慶応 東北大 中央大 神戸 早稲田 東北大 慶応 青学 青学 学習院 明治大 学習院 東北大 慶応 名大 立命館 早稲田 独協 九大 京大 九大 名大 阪大 東大 慶応 慶応 一橋 ・・・ ・・・ ・・・ ・・・ ・・・ ・・・ ・・・ ・・・ ・・・ ・・・ 日大 日大 日大 日大 お茶の水 九大 九大 北大 東大 早稲田 明治大 明治大 お茶の水 東大 慶応 立命館 慶応 北大 早稲田 早稲田 慶応 東北大 東北大 明治大 九大 阪大 京大 お茶の水 阪大 東大 worst1 worst2 worst3 worst4 worst5 best5 best4 best3 best2 best1 16 30 7 2 19 4 15 4 2 29 7 5 7 7 6 13 25 11 6 7 12 12 23 3 23 6 7 8 9 11 1 2 22 2 8 24 4 7 7 5 30 30 30 30 26 2 2 15 4 11 3 3 26 4 7 9 7 15 11 11 7 6 6 3 2 24 22 26 24 4 IDに置き換え
- 18. worst1 worst2 worst3worst4 worst5 best5 best4 best3 best2 best1 16 30 7 2 19 4 15 4 2 29 7 5 7 7 6 13 25 11 6 7 12 12 23 3 23 6 7 8 9 11 1 2 22 2 8 24 4 7 7 5 30 30 30 30 26 2 2 15 4 11 3 3 26 4 7 9 7 15 11 11 7 6 6 3 2 24 22 26 24 4 V 投票者 W職場の人数 U 大学の数
- 19. 統計モデリングの心得 1. 知りたいことを箇条書き＆優先順位づけ 2. それを知るためにいくつか可視化 3.シンプルなモデルから考える （データも少なくして）
- 20. 統計モデリングの心得 1. 知りたいことを箇条書き＆優先順位づけ 2. それを知るためにいくつか可視化 3.シンプルなモデルから考える （データも少なくして）
- 21.
- 22. 統計モデリングの心得 1. 知りたいことを箇条書き＆優先順位づけ 2. それを知るためにいくつか可視化 3.シンプルなモデルから考える （データも少なくして）
- 23. それを知るために可視化 使えるポイント − 使えないポイントの等高線 使えるポイント 使えるポイント ＋ 使えないポイント の等高線 (1100, 1000)と(100, 0)が同じランク… (100, 0)と(1, 0)が同じランク…
- 24.
- 25.
- 26. 統計モデリングの心得 1. 知りたいことを箇条書き＆優先順位づけ 2. それを知るためにいくつか可視化 3.シンプルなモデルから考える （データも少なくして）
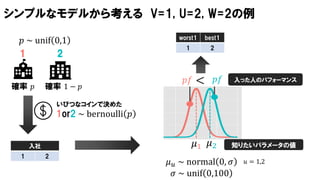
- 27. シンプルなモデルから考える V=1, U=2,W=2の例 確率 𝑝 確率 1 − 𝑝 1 2 𝑝 ~ unif 0,1 入社 1 2 いびつなコインで決めた 1or2 ~ bernoulli 𝑝 worst1 best1 1 2 𝜇1 𝜇2 𝑝𝑓 𝑝𝑓< 𝜇 𝑢 ~ normal 0, 𝜎 𝜎 ~ unif 0,100 入った人のパフォーマンス 𝑢 = 1,2 知りたいパラメータの値
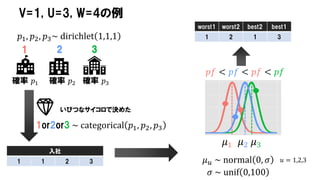
- 28. V=1, U=3, W=4の例 確率𝑝1 確率 𝑝2 1 2 𝑝1, 𝑝2, 𝑝3~ dirichlet 1,1,1 3 確率 𝑝3 入社 1 1 2 3 いびつなサイコロで決めた 1or2or3 ~ categorical 𝑝1, 𝑝2, 𝑝3 worst1 worst2 best2 best1 1 2 1 3 𝜇1 𝜇2 𝑝𝑓 < 𝑝𝑓 < 𝑝𝑓 < 𝑝𝑓 𝜇 𝑢 ~ normal 0, 𝜎 𝜇3 𝜎 ~ unif 0,100 𝑢 = 1,2,3
- 29. 最終的なモデル V=50, U=30, W=20に相当 𝑝1, 𝑝2, … , 𝑝 𝑈~ dirichlet 1,1, … , 1 𝜇 𝑢 ~ normal 0, 𝜎 𝜎 ~ unif 0,100 𝑼𝒏𝒊𝒗 𝒗,𝒘 ~ categorical 𝑝1, 𝑝2, … , 𝑝 𝑈 𝑝𝑓𝑣,𝑤 ~ normal 𝜇 𝑼𝒏𝒊𝒗 𝒗,𝒘 , 1 𝑝𝑓𝑣,1 < 𝑝𝑓𝑣,2 < ⋯ < 𝑝𝑓𝑣,𝑊 𝑣 = 1,2, … , 𝑉 が成り立つ時だけサンプリングを行う （その時だけ尤度に寄与があると考える） データは大学のインデックス𝑼𝒏𝒊𝒗 𝒗,𝒘だけ. 𝑢 = 1,2, … , 𝑈 𝑣 = 1,2, … , 𝑉 𝑤 = 1,2, … , 𝑊 𝑣 = 1,2, … , 𝑉 𝑤 = 1,2, … , 𝑊
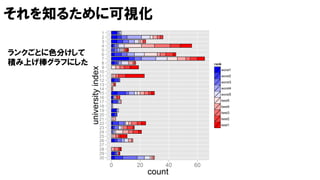
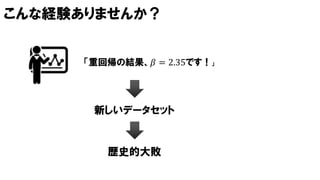
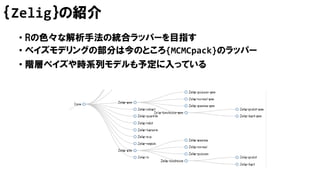
- 30. 実行 • {rstan}で実行しました. • 割愛しますがソースコード等は以下の記事になります. •[Stan]「使える大学・使えない大学」の事例から考えるアンケートの解析方法 • http://heartruptcy.blog.fc2.com/blog-entry-162.html
- 31. 結果 | 大学ごとの使える度合いの平均 ―:MCMCサンプルの95%信用区間 ●: MCMCサンプルの中央値
- 32. 結果 | 大学ごとの職場における存在確率 ―:MCMCサンプルの95%信用区間 ●: MCMCサンプルの中央値
- 33. まとめ • 久保緑本を読んでベイズモデリングをはじめてみよう • 解析のストーリーをたててからデータを取ろう •オレオレ指標のご利用は計画的に