Downloaded 56 times
![ごちゃごちゃしたこたぁ
いいんだよ！
men.h <- c(26.6,37.2,37.9,36.6,35.6,37.1,40.1,37.4,37.8,36.6)
mean.boot <- numeric(2000)
set.seed(314)
for (b in 1:2000){
i <- sample(1:10, replace=TRUE) # 1から10までの整数を10回無作為に抽出
men.boot <- men.h[i] # b回目のブートストラップ標本
mean.boot[b] <- mean(men.boot) # b回目のブートストラップ標本平均
}
hist(mean.boot, freq=F, xlab="bootstrap mean", main="") # 平均のヒストグラム
# 両側95%信頼区間
sort(mean.boot)[c(0.025*2000,0.975*2000)]](https://image.slidesharecdn.com/bootstrap-130228203258-phpapp02/75/R-8-2048.jpg)
![Jackknifeの失敗
x<-sample(1:100, size=10)
#標準誤差のジャックナイフ推定量
Jackknifeのmedianの標準誤差とBootstrap
M<-numeric(10) のmedianの標準誤差が大きく違う
for (i in 1:10){
y<-x[-i]
M[i]<-median(y)
}
何かおかしい！
Mbar<-mean(y)
print(sqrt((10-1)/10*sum((M-Mbar)^2)))
[1] 38.54363
#標準誤差のブートストラップ推定量 Jackknifeが推定誤差を起こす！
Mb<-replicate(1000, expr={
y<-sample(x, size=10, replace=T)
median(y)}
)
print(sd(Mb))
[1] 11.94611](https://image.slidesharecdn.com/bootstrap-130228203258-phpapp02/75/R-12-2048.jpg)
![回帰分析に応用
• こんなかんじのコンプライアンスとコレステロール値の散布図と3次の回帰直線
# データセットづくり
library(bootstrap)
# z の値を大きさの順でデータを並べ替える
zz <- sort(cholost$z)
yy <- cholost$y[order(cholost$z)]
# 拡大データフレームを作る
mydata <- data.frame(z1=zz, z2=zz^2, z3=zz^3, yy)
# データの散布図
plot(mydata$z1, mydata$yy,
xlab="compliance", ylab="decrease in cholesterol level")
# 最小2乗法による3次関数のあてはめ
cubic <- lm(yy~., data=mydata)
# 推定された回帰曲線を描く
lines(zz, predict(cubic), lty=2)](https://image.slidesharecdn.com/bootstrap-130228203258-phpapp02/75/R-22-2048.jpg)
![# データの散布図
plot(mydata$z1, mydata$yy, xlab=“compliance”, ylab=“decrease in cholesterol level”)
set.seed(314159) # 乱数の種を固定する
B <- 100 # ブートストラップ反復回数
n <- length(cholost$z) # 標本の大きさ
r60 <- numeric(B) # ブートストラップ回帰平均値
r100 <- numeric(B) # ブートストラップ回帰平均値
for (b in 1:100){ # ブートストラップ反復開始
bt <- sample(1:n, replace=TRUE) # ブートストラップ標本番号
mydata <- cholost[bt,] # ブートストラップ標本
zz <- sort(mydata$z) # zの値の並べ替え
yy <- mydata$y[order(mydata$z)] # zの大きさの順にyを並べ替える
mydata <- data.frame(z1=zz, z2=zz^2, z3=zz^3, yy) # データフレームを作る
cubic <- lm(yy~., data=mydata) # 最小2乗法による3次関数のあてはめ
lines(zz, predict(cubic)) # 求めた最小2乗曲線を描く
# z=60, 100 のときのブートストラップ回帰予測値
dumy <- predict(cubic, data.frame(z1=c(60, 100),
z2=c(60, 100)^2, z3=c(60, 100)^3))
r60[b] <- dumy[1]
r100[b] <- dumy[2]
}](https://image.slidesharecdn.com/bootstrap-130228203258-phpapp02/75/R-23-2048.jpg)
More Related Content
![[DL輪読会]Revisiting Deep Learning Models for Tabular Data (NeurIPS 2021) 表形式デー...](https://cdn.slidesharecdn.com/ss_thumbnails/dl20220318dlfin-220322065433-thumbnail.jpg?width=640&height=640&fit=bounds)
![[The Elements of Statistical Learning]Chapter8: Model Inferennce and Averaging](https://cdn.slidesharecdn.com/ss_thumbnails/theelementsofstatisticallearningchapter8modelinferennceandaveraging-181109001318-thumbnail.jpg?width=640&height=640&fit=bounds)
ブートストラップ法とその周辺とR
- 1. 計算統計学 〜Bootstrap法とその周辺〜 @ kingqwert
- 2. 複雑な問題 • 統計量の正確な標本分布の導出は困難 • 漸近理論の発展 o 最尤法 • 一致性、漸近正規性 • 漸近分散：Fisher情報量の逆数 • 統計量の関数の分布に関してはデルタ法 • 以下の様な統計量においては結構難しい o トリム平均、Median → 分位点に関する理論の発展が必要
- 3. Bootstrap法(ブーツの紐法) • 1979年 スタンフォード大のBradleyEfronにより開発 • 「ほら吹き男爵」の「ブーツの紐を引っ張って湖の底か ら脱出する」という話 • 教科書
- 4. Bootstrap法概説 • リサンプリングすることで母集団の分布を経験分布で代 用。ノンパラメトリックなモンテカルロ法の一種 • リサンプリング法では観測された標本を有限母集団とし て扱う • 標本＝擬似母集団からの無作為標本
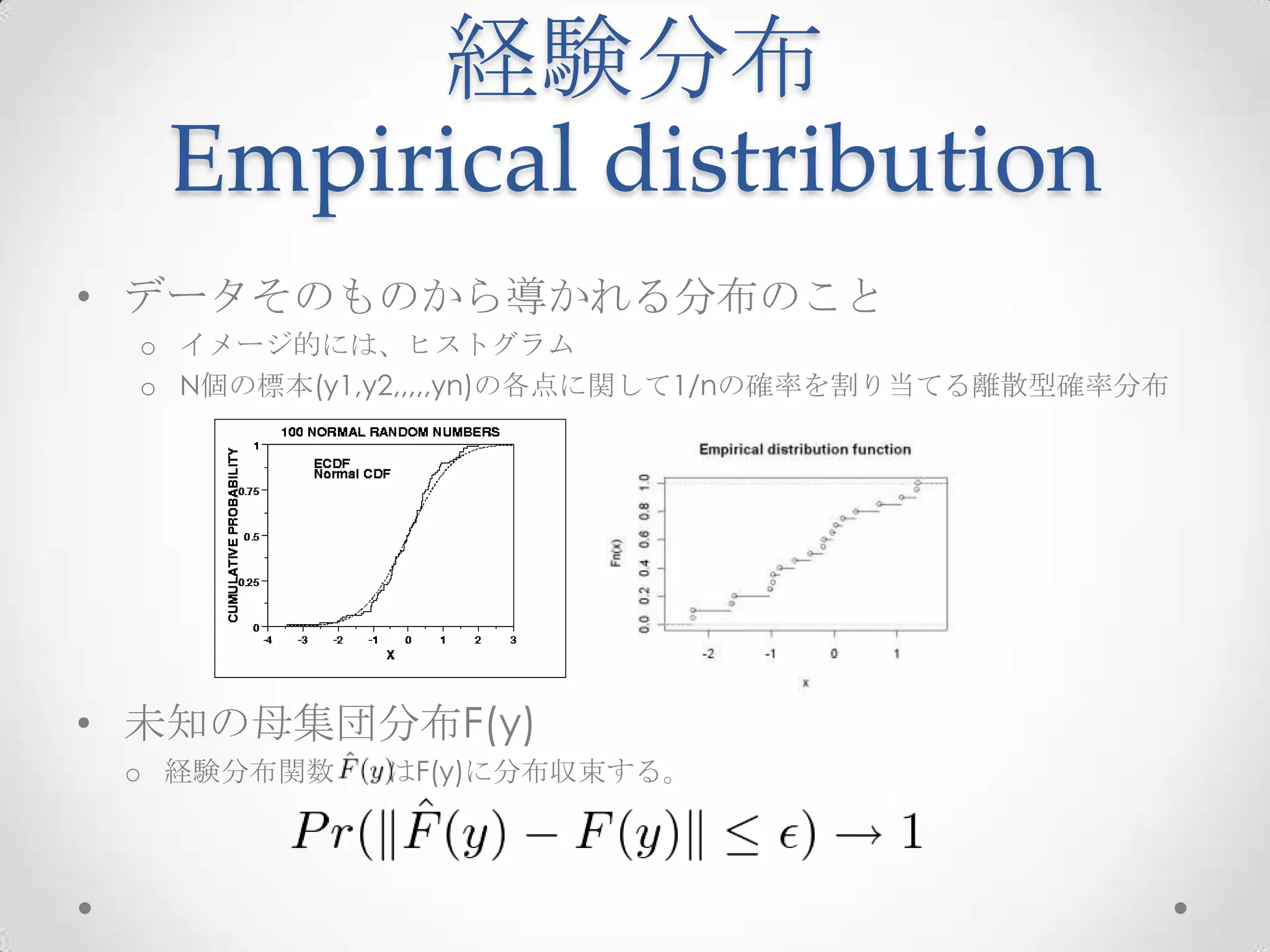
- 5. 経験分布 Empiricaldistribution • データそのものから導かれる分布のこと o イメージ的には、ヒストグラム o N個の標本(y1,y2,,,,,yn)の各点に関して1/nの確率を割り当てる離散型確率分布 • 未知の母集団分布F(y) o 経験分布関数 はF(y)に分布収束する。
- 6. 差込原理 • Plug-in estimator • を利用してパラメーターを推定する方法 o Bootstrap法はこの原理に基づいて計算される。 • Ex. 平均
- 7. 抽出方法 • 復元抽出 samplingwith replacement o 同じ要素の抽出を許す o Rコード： sample()関数 • Ex. sample(data, 100, replace =True) • 非復元抽出 sampling without replacement o 同じ要素の抽出を許さない o Rコード： sample()関数 • Ex. sample(data, 100, replace =False)
- 8. ごちゃごちゃしたこたぁ いいんだよ！ men.h <- c(26.6,37.2,37.9,36.6,35.6,37.1,40.1,37.4,37.8,36.6) mean.boot <- numeric(2000) set.seed(314) for (b in 1:2000){ i <- sample(1:10, replace=TRUE) # 1から10までの整数を10回無作為に抽出 men.boot <- men.h[i] # b回目のブートストラップ標本 mean.boot[b] <- mean(men.boot) # b回目のブートストラップ標本平均 } hist(mean.boot, freq=F, xlab="bootstrap mean", main="") # 平均のヒストグラム # 両側95%信頼区間 sort(mean.boot)[c(0.025*2000,0.975*2000)]
- 9. Cramér-Raoの下限と効率 • Fisher情報量(I(θ))の復習 o f(Y;θ)は尤度関数 o 意味：1回微分の分散か2回微分の期待値 • いくつかの正則条件のもとで o クラメール・ラオの下限 (ただし、 ) • の分散がクラメール・ラオの下限を達成するときに、 を有効推定量(Efficient estimator) o 最尤推定量が有効推定量であることは稀。通常は漸近的に達成（漸近有効）
- 10. ブートストラップ誤差 • 統計的誤差 o差込原理より として近似したことからくる誤差 o どうしようもないから諦めよう！（提案） o でも、nは大きくしようね！ • モンテカルロ誤差 o シミュレーションに基づく誤差 o 何回反復させるかに依存しているので、十分回数やろう！ o で、結局何回くらいが適当なの？ • nが大きい場合、反復回数を増やす • 中央値のような標本の滑らかなでない関数の場合反復回数を増やす o Efron and Tibshirani(1993) によると、分散や標準誤差のブートストラップ推定 の場合は25-300回程度十分らしい！
- 11. Jackknife法 • もう一つのリサンプリング法 o重複を許さないリサンプリング法 o 狭義にはこんなかんじで1つだけサンプルを抜いてリサンプリング o イメージ的にはCross validationによく似ている。 • どうでもいいけど、語源は「キャンプ場ですげー便利」 • 利点 o Bootstrapよりちょっと早い • 欠点 o 統計量が平滑でない値の場合、失敗する場合がある。（ex. Median） o 平滑性＝データの変化がどれくらい統計量を変化させるか
- 12. Jackknifeの失敗 x<-sample(1:100, size=10) #標準誤差のジャックナイフ推定量 Jackknifeのmedianの標準誤差とBootstrap M<-numeric(10) のmedianの標準誤差が大きく違う for (i in 1:10){ y<-x[-i] M[i]<-median(y) } 何かおかしい！ Mbar<-mean(y) print(sqrt((10-1)/10*sum((M-Mbar)^2))) [1] 38.54363 #標準誤差のブートストラップ推定量 Jackknifeが推定誤差を起こす！ Mb<-replicate(1000, expr={ y<-sample(x, size=10, replace=T) median(y)} ) print(sd(Mb)) [1] 11.94611
- 13. Bootstrap信頼区間 • 標準正規Bootstrap CI •基本Bootstrap CI • Percentile Bootstrap CI • Bootstrap T CI • BCa法 (Bias corrected and accelerated method) o 性能や特性など詳しくは、A.C. Davison et al(1997)
- 14. 標準正規/基本 B-CI • 標準正規CI o まぁ想像通りです。 o 仮定が強い • の分布が正規分布 or • が標本平均 and サンプルサイズが大きい（中心極限定理） • 基本CI o Bootstrap近似に基づく。 • と近似（この分位点を計算）→誤差が大きいかも o ただし、 の経験累積分布から標本のα分位点
- 15. Bootstrap T CI •基本Bootstrap CIの場合、 としているので、 分布のずれがある場合うまく行かない！ o 一次の正確度しかないから • 一次の正確度： • Cは被覆誤差 • C→0 (n→∞)がであってほしい 上側信頼限界 • それじゃ、二次のモーメント（分散）まで考えてみればいい じゃない！”t型”統計量の標本分布をリサンプリングで作成 • 信頼区間 o は、 のα/2番目に小さい値
- 16. Bootstrap T CI •信頼区間 o は、 のα/2番目に小さい値 • 長所 o 二次の正確性を持つ： • 短所 o σの推定が不可欠→ブートストラップ標本ごとにσを計算しなけれならないので、 計算負荷が大きい（つまり、ブートストラップのなかにブートストラップの入 れ子構造）
- 17. Percentile CI • みんな考えつく方法 • の分布で近似して、α/2番目に大きい値と (1-α)/2番目に大きい値を信頼区間とする • 信頼区間 • 欠点：一次の正確度しか持ってないけどね！
- 18. Percentile法の正確度 • Percentile CIの方が標準正規CIより良い被覆率 •変換後に左右対称となる の単調増加関数 が存在す るか否かに正確度が依存する。 o 多くの場合、そんな なんて存在しないよ！ • Efron and Tibshirani;1993 • 汪、桜井;2011 • ちょっと改善しましょ！→ BCa法
- 19. Bca法 • Percentile法を改善したもの • 分位点における、偏りに対する補正& 歪度（加速度）に対す る補正 • 変換後に以下を満たす単調増加関数 の存在を仮定 o b: 偏り修正定数 o a: 歪度（加速度）補正定数 • これで、分位点を補正！
- 20. BCa法 • 偏り補正定数＝ のMedianの偏りを補正 • 歪度(加速度)の補正定数 o ちなみに、加速度＝目標母数 に関して、 の標準誤差の変化率を推定する意味 • 二次の正確度を持つ！＝被覆誤差が で０に。
- 21. で、CI求めるのってどれがいいの & 何回反復すりゃいいの？ •うーん。Bootstrap-TかBCaかな? Byung-Jin Ahn et al; 2009 • CIの計算には分散の計算時よりも大きい反復回数が必要 o 90-95% CIの場合は反復回数1000-2000回は必要だよ！ • Efron and Tibshirani;1993
- 22. 回帰分析に応用 • こんなかんじのコンプライアンスとコレステロール値の散布図と3次の回帰直線 # データセットづくり library(bootstrap) # z の値を大きさの順でデータを並べ替える zz <- sort(cholost$z) yy <- cholost$y[order(cholost$z)] # 拡大データフレームを作る mydata <- data.frame(z1=zz, z2=zz^2, z3=zz^3, yy) # データの散布図 plot(mydata$z1, mydata$yy, xlab="compliance", ylab="decrease in cholesterol level") # 最小2乗法による3次関数のあてはめ cubic <- lm(yy~., data=mydata) # 推定された回帰曲線を描く lines(zz, predict(cubic), lty=2)
- 23. # データの散布図 plot(mydata$z1, mydata$yy,xlab=“compliance”, ylab=“decrease in cholesterol level”) set.seed(314159) # 乱数の種を固定する B <- 100 # ブートストラップ反復回数 n <- length(cholost$z) # 標本の大きさ r60 <- numeric(B) # ブートストラップ回帰平均値 r100 <- numeric(B) # ブートストラップ回帰平均値 for (b in 1:100){ # ブートストラップ反復開始 bt <- sample(1:n, replace=TRUE) # ブートストラップ標本番号 mydata <- cholost[bt,] # ブートストラップ標本 zz <- sort(mydata$z) # zの値の並べ替え yy <- mydata$y[order(mydata$z)] # zの大きさの順にyを並べ替える mydata <- data.frame(z1=zz, z2=zz^2, z3=zz^3, yy) # データフレームを作る cubic <- lm(yy~., data=mydata) # 最小2乗法による3次関数のあてはめ lines(zz, predict(cubic)) # 求めた最小2乗曲線を描く # z=60, 100 のときのブートストラップ回帰予測値 dumy <- predict(cubic, data.frame(z1=c(60, 100), z2=c(60, 100)^2, z3=c(60, 100)^3)) r60[b] <- dumy[1] r100[b] <- dumy[2] }