This document discusses techniques for semi-local string comparison, which involves comparing whole strings to substrings or prefixes to suffixes. It introduces implicit unit-Monge matrices, which allow efficient querying of string distances. Several algorithms are described that use these matrices, including the seaweed method and transposition network method.












![Introduction
Implicit unit-Monge matrices
Efficient P Σ queries: range tree on nonzeros of P [Bentley: 1980]
binary search tree by i-coordinate
under every node, binary search tree by j-coordinate
• • •
• −→ • −→ •
• • •
• • •
↓
• • •
• −→ • −→ •
• • •
• • •
↓
• • •
• −→ • −→ •
• • •
• • •
Alexander Tiskin (Warwick) Semi-local string comparison 8 / 132](https://image.slidesharecdn.com/20121020semi-localstringcomparisontiskin-121025075254-phpapp01/85/20121020-semi-local-string_comparison_tiskin-13-320.jpg)

![Introduction
Implicit unit-Monge matrices
Efficient P Σ queries: (contd.)
Every node of the range tree represents a canonical range (rectangular
region), and stores its nonzero count
Overall, ≤ n log n canonical ranges are non-empty
A P Σ query is equivalent to -dominance counting: how many nonzeros
are -dominated by query point?
Answer: sum up nonzero counts in ≤ log2 n disjoint canonical ranges
Total size O(n log n), query time O(log2 n)
There are asymptotically more efficient (but less practical) data structures
log n
Total size O(n), query time O log log n [J´J´+: 2004]
a a
[Chan, Pˇtra¸cu: 2010]
a s
Alexander Tiskin (Warwick) Semi-local string comparison 9 / 132](https://image.slidesharecdn.com/20121020semi-localstringcomparisontiskin-121025075254-phpapp01/85/20121020-semi-local-string_comparison_tiskin-15-320.jpg)









![Matrix distance multiplication
Seaweed braids
Related structures:
positive braids: far comm; braid relations
braids: gi gi−1 = 1; far comm; braid relations
Coxeter’s presentation of Sn : gi2 = 1; far comm; braid relations
locally free idempotent monoid: idem; far comm [Vershik+: 2000]
Generalisations:
general 0-Hecke monoids [Fomin, Greene: 1998; Buch+: 2008]
Coxeter monoids [Tsaranov: 1990; Richardson, Springer: 1990]
J -trivial monoids [Denton+: 2011]
Alexander Tiskin (Warwick) Semi-local string comparison 16 / 132](https://image.slidesharecdn.com/20121020semi-localstringcomparisontiskin-121025075254-phpapp01/85/20121020-semi-local-string_comparison_tiskin-25-320.jpg)





![Matrix distance multiplication
Seaweed matrix multiplication
The implicit unit-Monge matrix -multiplication problem
Given permutation matrices PA , PB , compute PC , such that
Σ Σ Σ
PA PB = PC (equivalently, PA PB = PC )
Matrix -multiplication: running time
type time
general O(n3 ) standard
3 3
O n (log log n)
log2 n
[Chan: 2007]
Monge O(n2 ) via [Aggarwal+: 1987]
implicit unit-Monge O(n1.5 ) [T: 2006]
O(n log n) [T: 2010]
Alexander Tiskin (Warwick) Semi-local string comparison 18 / 132](https://image.slidesharecdn.com/20121020semi-localstringcomparisontiskin-121025075254-phpapp01/85/20121020-semi-local-string_comparison_tiskin-31-320.jpg)









![Matrix distance multiplication
Bruhat order
Bruhat comparability: running time
O(n2 ) folklore
O(n log n) [T: NEW]
PA PB iff PA ≤ PB elementwise, time O(n2 )
Σ Σ folklore
R R
PA PB iff PA PB = Id , time O(n log n) [T: NEW]
where P R denotes clockwise rotation of matrix P
Alexander Tiskin (Warwick) Semi-local string comparison 25 / 132](https://image.slidesharecdn.com/20121020semi-localstringcomparisontiskin-121025075254-phpapp01/85/20121020-semi-local-string_comparison_tiskin-42-320.jpg)




![Semi-local string comparison
Semi-local LCS and edit distance
The LCS problem
Give the LCS score for a vs b
LCS: running time
O(mn) [Wagner, Fischer: 1974]
mn
O log2 n σ = O(1) [Masek, Paterson: 1980]
[Crochemore+: 2003]
mn(log log n)2
O log2 n
[Paterson, Danˇ´cık: 1994]
[Bille, Farach-Colton: 2008]
Running time varies depending on the RAM model version
We assume word-RAM with word size log n (where it matters)
Alexander Tiskin (Warwick) Semi-local string comparison 28 / 132](https://image.slidesharecdn.com/20121020semi-localstringcomparisontiskin-121025075254-phpapp01/85/20121020-semi-local-string_comparison_tiskin-47-320.jpg)

![Semi-local string comparison
Semi-local LCS and edit distance
LCS: dynamic programming [WF: 1974]
Sweep cells in any -compatible order
Cell update: time O(1)
Overall time O(mn)
Alexander Tiskin (Warwick) Semi-local string comparison 30 / 132](https://image.slidesharecdn.com/20121020semi-localstringcomparisontiskin-121025075254-phpapp01/85/20121020-semi-local-string_comparison_tiskin-49-320.jpg)



![Semi-local string comparison
Semi-local LCS and edit distance
LCS: micro-block dynamic programming [MP: 1980; BF: 2008]
Sweep cells in micro-blocks, in any -compatible order
Micro-block size:
t = O(log n) when σ = O(1)
log n
t=O log log n otherwise
Micro-block interface:
O(t) characters, each O(log σ) bits, can be reduced to O(log t) bits
O(t) small integers, each O(1) bits
Micro-block update: time O(1), by precomputing all possible interfaces
mn mn(log log n)2
Overall time O log2 n
when σ = O(1), O log2 n
otherwise
Alexander Tiskin (Warwick) Semi-local string comparison 33 / 132](https://image.slidesharecdn.com/20121020semi-localstringcomparisontiskin-121025075254-phpapp01/85/20121020-semi-local-string_comparison_tiskin-53-320.jpg)




![Semi-local string comparison
Score matrices and seaweed matrices
Semi-local LCS: output representation and running time
size query time
O(n2 ) O(1) trivial
O(m1/2 n) O(log n) string-substring [Alves+: 2003]
O(n) O(n) string-substring [Alves+: 2005]
O(n log n) O(log2 n) [T: 2006]
. . . or any 2D orthogonal range counting data structure
running time
O(mn2 ) naive
O(mn) string-substring [Schmidt: 1998; Alves+: 2005]
O(mn) [T: 2006]
mn
O log0.5 n [T: 2006]
mn(log log n)2
O log2 n
[T: 2007]
Alexander Tiskin (Warwick) Semi-local string comparison 37 / 132](https://image.slidesharecdn.com/20121020semi-localstringcomparisontiskin-121025075254-phpapp01/85/20121020-semi-local-string_comparison_tiskin-58-320.jpg)

















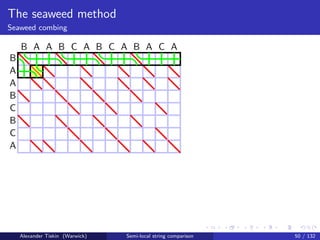




































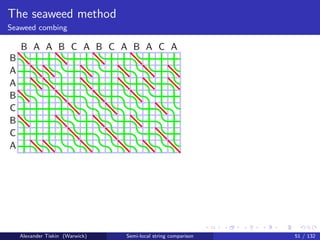
![The seaweed method
Seaweed combing
Semi-local LCS: seaweed combing [T: 2006]
Initialise seaweed braid: crossings in all mismatch cells
Sweep cells in any -compatible order
Match cell: two seaweeds uncrossed; skip
Mismatch cell: two seaweeds cross
if the same seaweeds crossed before, uncross them
otherwise skip, keep seaweeds crossed
Cell update: time O(1)
Overall time O(mn)
Alexander Tiskin (Warwick) Semi-local string comparison 52 / 132](https://image.slidesharecdn.com/20121020semi-localstringcomparisontiskin-121025075254-phpapp01/85/20121020-semi-local-string_comparison_tiskin-114-320.jpg)













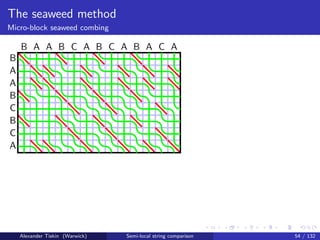

![The seaweed method
Micro-block seaweed combing
Semi-local LCS: micro-block seaweed combing [T: 2007]
Initialise seaweed braid: crossings in all mismatch cells
Sweep cells in micro-blocks, in any -compatible order
log n
Micro-block size: t = O log log n
Micro-block interface:
O(t) characters, each O(log σ) bits, can be reduced to O(log t) bits
O(t) integers, each O(log n) bits, can be reduced to O(log t) bits
Micro-block update: time O(1), by precomputing all possible interfaces
mn(log log n)2
Overall time O log2 n
Alexander Tiskin (Warwick) Semi-local string comparison 56 / 132](https://image.slidesharecdn.com/20121020semi-localstringcomparisontiskin-121025075254-phpapp01/85/20121020-semi-local-string_comparison_tiskin-130-320.jpg)

![The seaweed method
Cyclic LCS
The cyclic LCS problem
Give the maximum LCS score for a vs all cyclic rotations of b
Cyclic LCS: running time
mn 2
O log n naive
O(mn log m) [Maes: 1990]
O(mn) [Bunke, B¨hler: 1993; Landau+: 1998; Schmidt: 1998]
u
2
O mn(log 2log n)
log n
[T: 2007]
Alexander Tiskin (Warwick) Semi-local string comparison 57 / 132](https://image.slidesharecdn.com/20121020semi-localstringcomparisontiskin-121025075254-phpapp01/85/20121020-semi-local-string_comparison_tiskin-132-320.jpg)


![The seaweed method
Longest repeating subsequence
The longest repeating subsequence problem
Find the longest subsequence of a that is a square (a repetition of two
identical strings)
Longest repeating subsequence: running time
O(m3 ) naive
O(m2 ) [Kosowski: 2004]
2 log 2
O m (log 2 m m)
log
[T: 2007]
Alexander Tiskin (Warwick) Semi-local string comparison 59 / 132](https://image.slidesharecdn.com/20121020semi-localstringcomparisontiskin-121025075254-phpapp01/85/20121020-semi-local-string_comparison_tiskin-135-320.jpg)

![The seaweed method
Approximate matching
The approximate pattern matching problem
Give the substring closest to a by alignment score, starting at each
position in b
Assume rational alignment score
Approximate pattern matching: running time
O(mn) [Sellers: 1980]
mn
O log n σ = O(1) via [Masek, Paterson: 1980]
mn(log log n)2
O log2 n
via [Bille, Farach-Colton: 2008]
Alexander Tiskin (Warwick) Semi-local string comparison 61 / 132](https://image.slidesharecdn.com/20121020semi-localstringcomparisontiskin-121025075254-phpapp01/85/20121020-semi-local-string_comparison_tiskin-137-320.jpg)
![The seaweed method
Approximate matching
Approximate pattern matching: the algorithm
Micro-block seaweed combing on a vs b (with blow-up), time
2
O mn(log 2log n)
log n
The implicit semi-local edit score matrix:
an anti-Monge matrix
approximate pattern matching ∼ row minima
Row minima in O(n) element queries [Aggarwal+: 1987]
Each query in time O(log2 n) using the range tree representation,
combined query time negligible
mn(log log n)2
Overall running time O log2 n
, same as [Bille, Farach-Colton: 2008]
Alexander Tiskin (Warwick) Semi-local string comparison 62 / 132](https://image.slidesharecdn.com/20121020semi-localstringcomparisontiskin-121025075254-phpapp01/85/20121020-semi-local-string_comparison_tiskin-138-320.jpg)






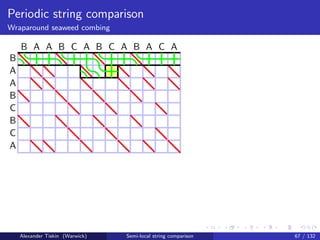












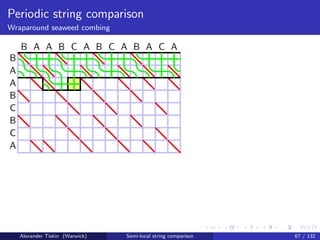


























![Periodic string comparison
Wraparound seaweed combing
The tandem LCS problem
Give LCS score for a vs b = u k
We have n = kp; may assume k ≤ m
Tandem LCS: running time
O(mkp) naive
O m(k + p) [Landau, Ziv-Ukelson: 2001]
O(mp) [T: 2009]
Direct application of wraparound seaweed combing
Alexander Tiskin (Warwick) Semi-local string comparison 70 / 132](https://image.slidesharecdn.com/20121020semi-localstringcomparisontiskin-121025075254-phpapp01/85/20121020-semi-local-string_comparison_tiskin-185-320.jpg)
![Periodic string comparison
Wraparound seaweed combing
The tandem alignment problem
Give the substring closest to a by alignment score among certain
substrings of b = u ±∞ :
global: substrings u k of length kp across all k
cyclic: substrings of length kp across all k
local: substrings of any length
Tandem alignment: running time
O(m2 p) all naive
O(mp) global [Myers, Miller: 1989]
O(mp log p) cyclic [Benson: 2005]
O(mp) cyclic [T: 2009]
O(mp) local [Myers, Miller: 1989]
Alexander Tiskin (Warwick) Semi-local string comparison 71 / 132](https://image.slidesharecdn.com/20121020semi-localstringcomparisontiskin-121025075254-phpapp01/85/20121020-semi-local-string_comparison_tiskin-186-320.jpg)
![Periodic string comparison
Wraparound seaweed combing
Cyclic tandem alignment: the algorithm
Periodic seaweed combing for a vs b (with blow-up), time O(mp)
For each k ∈ [1 : m]:
solve tandem LCS (under given alignment score) for a vs u k
obtain scores for a vs p successive substrings of b of length kp by LCS
batch query: time O(1) per substring
Running time O(mp)
Alexander Tiskin (Warwick) Semi-local string comparison 72 / 132](https://image.slidesharecdn.com/20121020semi-localstringcomparisontiskin-121025075254-phpapp01/85/20121020-semi-local-string_comparison_tiskin-187-320.jpg)


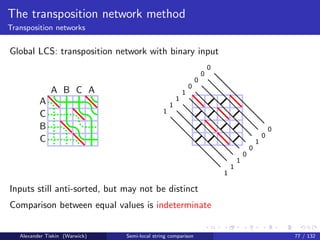
![The transposition network method
Transposition networks
Comparison network: a circuit of comparators
A comparator sorts two inputs and outputs them in prescribed order
Comparison networks traditionally used for non-branching merging/sorting
Classical comparison networks
# comparators
merging O(n log n) [Batcher: 1968]
sorting O(n log2 n) [Batcher: 1968]
O(n log n) [Ajtai+: 1983]
Alexander Tiskin (Warwick) Semi-local string comparison 75 / 132](https://image.slidesharecdn.com/20121020semi-localstringcomparisontiskin-121025075254-phpapp01/85/20121020-semi-local-string_comparison_tiskin-190-320.jpg)
![The transposition network method
Transposition networks
Comparison network: a circuit of comparators
A comparator sorts two inputs and outputs them in prescribed order
Comparison networks traditionally used for non-branching merging/sorting
Classical comparison networks
# comparators
merging O(n log n) [Batcher: 1968]
sorting O(n log2 n) [Batcher: 1968]
O(n log n) [Ajtai+: 1983]
Comparison networks are visualised by wire diagrams
Transposition network: all comparisons are between adjacent wires
Alexander Tiskin (Warwick) Semi-local string comparison 75 / 132](https://image.slidesharecdn.com/20121020semi-localstringcomparisontiskin-121025075254-phpapp01/85/20121020-semi-local-string_comparison_tiskin-191-320.jpg)



![The transposition network method
Parameterised string comparison
Parameterised string comparison: running time
Low-similarity, after preprocessing in O(n log σ)
O(nλ) [Hirschberg: 1977]
[Apostolico, Guerra: 1985]
[Apostolico+: 1992]
High-similarity, no preprocessing
O(n · κ) [Ukkonen: 1985]
[Myers: 1986]
Flexible
O(λ · κ · log n) no preproc [Myers: 1986; Wu+: 1990]
O(λ · κ) after preproc [Rick: 1995]
Alexander Tiskin (Warwick) Semi-local string comparison 80 / 132](https://image.slidesharecdn.com/20121020semi-localstringcomparisontiskin-121025075254-phpapp01/85/20121020-semi-local-string_comparison_tiskin-196-320.jpg)


![The transposition network method
Dynamic string comparison
Dynamic LCS in linear time: update models
left right
– app+del standard DP [Wagner, Fischer: 1974]
app app a fixed [Landau+: 1998], [Kim, Park: 2004]
app app [Ishida+: 2005]
app+del app+del [T: NEW]
Main idea:
for append only, maintain seaweed matrix Pa,b
for append+delete, maintain partial seaweed layout by tracing a
transposition network
Alexander Tiskin (Warwick) Semi-local string comparison 83 / 132](https://image.slidesharecdn.com/20121020semi-localstringcomparisontiskin-121025075254-phpapp01/85/20121020-semi-local-string_comparison_tiskin-199-320.jpg)
![The transposition network method
Bit-parallel string comparison
Bit-parallel string comparison
String comparison using standard instructions on words of size w
Bit-parallel string comparison: running time
O(mn/w ) [Allison, Dix: 1986; Myers: 1999; Crochemore+: 2001]
Alexander Tiskin (Warwick) Semi-local string comparison 84 / 132](https://image.slidesharecdn.com/20121020semi-localstringcomparisontiskin-121025075254-phpapp01/85/20121020-semi-local-string_comparison_tiskin-200-320.jpg)




![Sparse string comparison
Semi-local LCS between permutations
The LCS problem on permutation strings
Give LCS score for a vs b
In each of a, b all characters distinct: total m = n matches
Equivalent to
longest increasing subsequence (LIS) in a string
maximum clique in a permutation graph
maximum planar matching in an embedded bipartite graph
LCS on permutation strings: running time
O(n log n) implicit in [Erd¨s, Szekeres:
o 1935]
[Robinson: 1938; Knuth: 1970; Dijkstra: 1980]
O(n log log n) unit-RAM [Chang, Wang: 1992]
[Bespamyatnikh, Segal: 2000]
Alexander Tiskin (Warwick) Semi-local string comparison 88 / 132](https://image.slidesharecdn.com/20121020semi-localstringcomparisontiskin-121025075254-phpapp01/85/20121020-semi-local-string_comparison_tiskin-205-320.jpg)
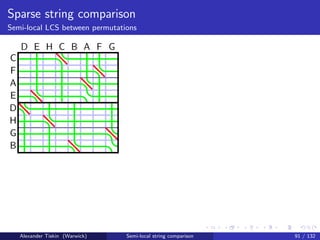
![Sparse string comparison
Semi-local LCS between permutations
The semi-local LCS problem on permutation strings
Give semi-local LCS scores of a vs b
In each of a, b all characters distinct: total m = n matches
Equivalent to
longest increasing subsequence (LIS) in every substring of a string
Semi-local LCS on permutation strings: running time
O(n2 log n) naive
O(n2 ) restricted [Albert+: 2003; Chen+: 2005]
O(n1.5 log n) randomised, restricted [Albert+: 2007]
O(n1.5 ) [T: 2006]
O(n log2 n) [T: NEW]
Alexander Tiskin (Warwick) Semi-local string comparison 89 / 132](https://image.slidesharecdn.com/20121020semi-localstringcomparisontiskin-121025075254-phpapp01/85/20121020-semi-local-string_comparison_tiskin-206-320.jpg)






![Sparse string comparison
Longest piecewise monotone subsequences
A k-increasing sequence: a concatenation of k increasing sequences
A k-modal sequence: a concatenation of k alternating increasing and
decreasing sequences
The longest k-increasing (k-modal) subsequence problem
Give the longest k-increasing (k-modal) subsequence of string b
Longest k-increasing (k-modal) subsequence: running time
O(nk log n) k-modal [Demange+: 2007]
O(nk log n) via [Hunt, Szymanski: 1977]
O(n log2 n) [T: NEW]
Main idea: LCS for id k (respectively, (idid)k/2 ) vs b
Alexander Tiskin (Warwick) Semi-local string comparison 94 / 132](https://image.slidesharecdn.com/20121020semi-localstringcomparisontiskin-121025075254-phpapp01/85/20121020-semi-local-string_comparison_tiskin-214-320.jpg)




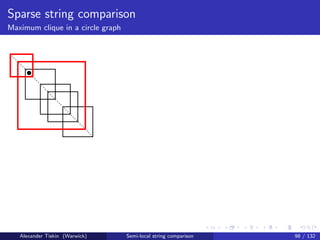
![Sparse string comparison
Maximum clique in a circle graph
Maximum clique in a circle graph: running time
exp(n) naive
O(n3 ) [Gavril: 1973]
O(n2 ) [Rotem, Urrutia: 1981; Hsu: 1985]
[Masuda+: 1990; Apostolico+: 1992]
O(n1.5 ) [T: 2006]
O(n log2 n) [T: NEW]
Alexander Tiskin (Warwick) Semi-local string comparison 97 / 132](https://image.slidesharecdn.com/20121020semi-localstringcomparisontiskin-121025075254-phpapp01/85/20121020-semi-local-string_comparison_tiskin-219-320.jpg)











![Sparse string comparison
Maximum clique in a circle graph
Parameterised maximum clique in a circle graph
The maximum clique problem in a circle graph, sensitive e.g. to
the number e of edges
the size l of maximum clique
the thickness d of interval model (the maximum number of intervals
covering a point)
We have l ≤ d ≤ n, e ≤ n2
Parameterised maximum clique in a circle graph: running time
O(n log n + e) [Apostolico+: 1992]
O(n log n + nl log(n/l)) [Apostolico+: 1992]
O(n log n + n log2 d) NEW
Alexander Tiskin (Warwick) Semi-local string comparison 100 / 132](https://image.slidesharecdn.com/20121020semi-localstringcomparisontiskin-121025075254-phpapp01/85/20121020-semi-local-string_comparison_tiskin-232-320.jpg)





![Compressed string comparison
Extended substring-string LCS on GC-strings
LCS: running time (r = m + n, ¯ = m + n)
r ¯ ¯
p t
plain plain O(mn) [Wagner, Fischer: 1974]
mn
O log2 m [Masek, Paterson: 1980]
[Crochemore+: 2003]
plain GC O(m3 n + . . .)
¯ gen. CFG [Myers: 1995]
O(m ¯1.5 n) ext subs-s [T: 2008]
O(m log m · n) ¯ ext subs-s [T: 2010]
GC GC NP-hard [Lifshits: 2005]
O(r 1.2¯1.4 )
r R weights [Hermelin+: 2009]
O(r log r · ¯)
r [T: 2010]
O r log(r /¯) · ¯
r r [Hermelin+: 2010]
O r log1/2 (r /¯) · ¯
r r [Gawrychowski: NEW]
Alexander Tiskin (Warwick) Semi-local string comparison 106 / 132](https://image.slidesharecdn.com/20121020semi-localstringcomparisontiskin-121025075254-phpapp01/85/20121020-semi-local-string_comparison_tiskin-238-320.jpg)

![Compressed string comparison
Subsequence recognition on GC-strings
The global subsequence recognition problem
Does pattern p appear in text t as a subsequence?
Global subsequence recognition: running time
p t
plain plain O(n) greedy
plain GC O(m¯)
n greedy
GC GC NP-hard [Lifshits: 2005]
Alexander Tiskin (Warwick) Semi-local string comparison 108 / 132](https://image.slidesharecdn.com/20121020semi-localstringcomparisontiskin-121025075254-phpapp01/85/20121020-semi-local-string_comparison_tiskin-240-320.jpg)

![Compressed string comparison
Subsequence recognition on GC-strings
Local subsequence recognition: running time ( + output)
p t
plain plain O(mn) [Mannila+: 1995]
mn
O log m [Das+: 1997]
O(c m + n) [Boasson+: 2001]
O(m + nσ) [Troniˇek: 2001]
c
plain GC O(m2 log m¯)
n [C´gielski+: 2006]
e
1.5 n)
O(m ¯ [T: 2008]
O(m log m · n)
¯ [T: NEW]
GC GC NP-hard [Lifshits: 2005]
Alexander Tiskin (Warwick) Semi-local string comparison 110 / 132](https://image.slidesharecdn.com/20121020semi-localstringcomparisontiskin-121025075254-phpapp01/85/20121020-semi-local-string_comparison_tiskin-242-320.jpg)
![Compressed string comparison
Subsequence recognition on GC-strings
0 ˆ0+
ı ˆ1+
ı ˆ2+
ı n n
0+
ˆ 1+
ˆ 2+
ˆ
b i : j matching iff box [i : j] not pierced left-to-right
-maximal seaweeds: -chain ˆ0+ , 0+
ı ˆ ˆ1+ , 1+
ı ˆ ··· ˆs − , s −
ı ˆ
b i : j minimally matching iff (i, j) is in the interleaved -chain
ˆ− , +
ı1+ ˆ1− ˆ− , +
ı2+ ˆ2− ··· ˆ− + , + −
ı(s−1) ˆ(s−1)
Alexander Tiskin (Warwick) Semi-local string comparison 111 / 132](https://image.slidesharecdn.com/20121020semi-localstringcomparisontiskin-121025075254-phpapp01/85/20121020-semi-local-string_comparison_tiskin-243-320.jpg)





![Compressed string comparison
Threshold approximate matching
Threshold approximate matching: running time ( + output)
p t
plain plain O(mn) [Sellers: 1980]
O(mk) [Landau, Vishkin: 1989]
4
O(m + n + nk )
m [Cole, Hariharan: 2002]
plain GC O(m¯k 2 )
n [K¨rkk¨inen+: 2003]
a a
O(m¯k + n log n)
n ¯ [LV: 1989] via [Bille+: 2010]
O(m¯ + nk 4 + n log n)
n ¯ ¯ [CH: 2002] via [Bille+: 2010]
O(m log m · n)
¯ [T: NEW]
GC GC NP-hard [Lifshits: 2005]
(Also many specialised variants for LZ compression)
Alexander Tiskin (Warwick) Semi-local string comparison 115 / 132](https://image.slidesharecdn.com/20121020semi-localstringcomparisontiskin-121025075254-phpapp01/85/20121020-semi-local-string_comparison_tiskin-249-320.jpg)
![Compressed string comparison
Threshold approximate matching
Threshold approx matching (plain pattern, GC text): the algorithm
Algorithm structure similar to local subsequence recognition by matrix
-multiplication and seaweed -chains
Extra ingredients:
the blow-up technique: reduction of edit distances to LCS scores
implicit matrix searching, replaces -chain interleaving
Monge row minima: “SMAWK” O(m) [Aggarwal+: 1987]
Implicit unit-Monge row minima O(m log log m) [T: NEW]
O(m) [Gawrychowski: NEW]
replaces -chain interleaving
Overall time O(m log m · n) + O(m¯) = O(m log m · n)
¯ n ¯
Alexander Tiskin (Warwick) Semi-local string comparison 116 / 132](https://image.slidesharecdn.com/20121020semi-localstringcomparisontiskin-121025075254-phpapp01/85/20121020-semi-local-string_comparison_tiskin-250-320.jpg)




![Beyond semi-locality
Window-local LCS and alignment plots
Given window length w
The window-local LCS problem
Give semi-local LCS score for every w -substring of a vs whole b
Window-local LCS: running time
O(mn3 w ) naive
O(mnw ) multiple seaweed
O(mn) [Krusche, T: 2010]
Alexander Tiskin (Warwick) Semi-local string comparison 120 / 132](https://image.slidesharecdn.com/20121020semi-localstringcomparisontiskin-121025075254-phpapp01/85/20121020-semi-local-string_comparison_tiskin-255-320.jpg)


![Beyond semi-locality
Window-local LCS and alignment plots
The window-window LCS problem
Give semi-local LCS score for every w -substring of a vs every w -substring b
Provides an alignment plot: loss-free local comparison of genome
sequences, important for studying conservation in the genome
Window-window LCS: running time
O(mnw 2 ) naive
O(mnw ) multiple seaweed
O(mn) [Krusche, T: 2010]
Alexander Tiskin (Warwick) Semi-local string comparison 122 / 132](https://image.slidesharecdn.com/20121020semi-localstringcomparisontiskin-121025075254-phpapp01/85/20121020-semi-local-string_comparison_tiskin-258-320.jpg)
![Beyond semi-locality
Window-local LCS and alignment plots
An implementation of alignment plots [Krusche: 2010]
Based on the O(mnw ) multiple seaweed combing, using some ideas from
the optimal O(mn) algorithm
Resulting theoretical complexity O(mnw 0.5 )
Alignment weights (match 1, mismatch 0, gap −0.5): ×4 slowdown
C++, Intel assembly (x86, x86 64, MMX/SSE2 data parallelism)
SMP parallelism (currently two processors)
Alexander Tiskin (Warwick) Semi-local string comparison 123 / 132](https://image.slidesharecdn.com/20121020semi-localstringcomparisontiskin-121025075254-phpapp01/85/20121020-semi-local-string_comparison_tiskin-259-320.jpg)

![Beyond semi-locality
Window-local LCS and alignment plots
Publications:
[Picot+: 2010] Evolutionary Analysis of Regulatory Sequences (EARS) in
Plants. Plant Journal.
[Baxter+: accepted] Conserved Noncoding Sequences Highlight Shared
Components of Regulatory Networks in Dicotyledonous Plants. Plant Cell.
Web service: http://wsbc.warwick.ac.uk/ears
Future work: genomic repeats; genome-scale comparison
Alexander Tiskin (Warwick) Semi-local string comparison 125 / 132](https://image.slidesharecdn.com/20121020semi-localstringcomparisontiskin-121025075254-phpapp01/85/20121020-semi-local-string_comparison_tiskin-261-320.jpg)

![Beyond semi-locality
Quasi-local LCS and sparse spliced alignment
Given m (possibly overlapping) prescribed substrings in a
The quasi-local LCS problem
Give semi-local LCS score for every prescribed substring of a vs whole b
Quasi-local LCS: running time
O(m2 n) multiple seaweed
O(mn log2 m) [T: unpublished]
Alexander Tiskin (Warwick) Semi-local string comparison 126 / 132](https://image.slidesharecdn.com/20121020semi-localstringcomparisontiskin-121025075254-phpapp01/85/20121020-semi-local-string_comparison_tiskin-263-320.jpg)


![Beyond semi-locality
Quasi-local LCS and sparse spliced alignment
The sparse spliced alignment problem
Give the chain of non-overlapping prescribed substrings in a, closest to b
by alignment score
Describes gene assembly: unknown gene from candidate exons, given a
known similar gene
Assume m = n; let s = total size of prescribed substrings
Sparse spliced alignment: running time
O(ns) = O(n3 ) [Gelfand+: 1996]
O(n2.5 ) [Kent+: 2006]
O(n2 log2 n) [T: unpublished]
O(n2 log n) [Sakai: 2009]
Alexander Tiskin (Warwick) Semi-local string comparison 128 / 132](https://image.slidesharecdn.com/20121020semi-localstringcomparisontiskin-121025075254-phpapp01/85/20121020-semi-local-string_comparison_tiskin-266-320.jpg)



