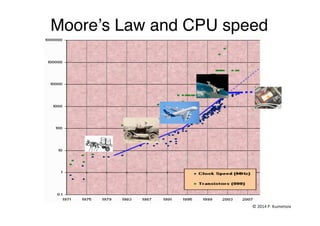
The document discusses concurrency and synchronization in distributed computing. It provides an overview of Petr Kuznetsov's research at Telecom ParisTech, which includes algorithms and models for distributed systems. Some key points discussed are: - Concurrency is important due to multi-core processors and distributed systems being everywhere. However, synchronization between concurrent processes introduces challenges. - Common synchronization problems include mutual exclusion, readers-writers problems, and producer-consumer problems. Tools for synchronization include semaphores, transactional memory, and non-blocking algorithms. - Characterizing distributed computing models and determining what problems can be solved in a given model is an important area of research, with implications for distributed system design.

1.
Mathematics in Synchronization and
Concurrency
"
Petr Kuznetsov"
Telecom ParisTech"
"
"
Algorithmic methods laboratory, PDMI, SPb, 2014"
"

2. Télécom ParisTech"
§ A.k.a. ENST (École nationale supérieure des
télécommunications)"
§ Member of ParisTech and Mines-Telecom ""
§ One the most known “grandes écoles”"
§ One of the founders of Eurécom"
§ Research labs:"
ü INFRES – computer science and networking"
ü COMELEC – electronics and communication"
ü TSI – signal and image processing "
ü SES – economics and social sciences"
§ Research internship/PhD at INFRES:
petr.kuznetsov@telecom-paristech.fr"
©
2014
P.
Kuznetsov

3. "
"
What is computing?"
"

4. "
"
What is done by a Turing machine"
"
"
"
"

5. "
Not well adjusted to concurrency?"
"
Computation as interaction"
"
Robin Milner"
1934-2010"

6. "
"
Distributed computing model:"
independent sequential processes
that communicate"
"
"
©
2014
P.
Kuznetsov

7. Concurrency is everywhere!"
§ Sensor networks"
§ Internet"
§ Basically everything
related computing"
• Multi-core processors"
©
2014
P.
Kuznetsov

8. Moore’s Law and CPU speed"
©
2014
P.
Kuznetsov

11.
“washing machine science”?"
§ Single-processor performance does
not improve"
§ But we can add more cores"
§ Run concurrent code on multiple
processors"
Can we expect a proportional
speedup? (ratio between sequential
time and parallel time for executing
a job)"
©
2014
P.
Kuznetsov

12. Example: painting in parallel"
§ 3 friends want to paint 3 equal-size walls, one
friend per wall"
ü Speedup = 3"
"
§ What if one wall is twice as big?"
©
2014
P.
Kuznetsov

13. Amdahl’s Law"
§ p – fraction of the work that can be done in
parallel (no synchronization)"
§ n - the number of processors"
§ Time one processor needs to complete the
job = 1"
©
2014
P.
Kuznetsov

14. A better solution"
§ When done, help the others "
ü All 3 paint the remaining half-room in parallel "
§ Communication and agreement is required!"
§ This is a hard task!
§ Synchronization algorithms!"
"
©
2014
P.
Kuznetsov

15. Why synchronize ?"
§ Concurrent accesses to a shared resource (e.g., a file) may
lead to an inconsistent state "
ü Non-deterministic result (race condition): the resulting state
depends on the scheduling"
§ Concurrent accesses need to be synchronized!
ü E. g., decide who is allowed to update a given part of the file at a
given time"
§ Code leading to a race condition is called critical section!
ü Must be (or appear to be) executed sequentially"
§ Synchronization problems: mutual exclusion, readers-
writers, producer-consumer, …"
§ Synchronization abstractions: semaphores, TAS, CAS,
queues, skip-lists, dictionaries, transactional memory "
©
2014
P.
Kuznetsov

16. Challenges"
§ What is correct?"
ü Safety and liveness"
§ What is the cost of synchronization?"
ü Time and space lower bounds"
§ Failures/asynchrony"
ü Fault-tolerant synchronization?"
§ How to distinguish possible from impossible? "
ü Impossibility results"
"
©
2014
P.
Kuznetsov

17. Distributed ≠ Parallel"
§ The main challenge is synchronization despite
uncertainty (failures, asynchrony)"
"
§ “you know you have a distributed system
when the crash of a computer you’ve never
heard of stops you from getting any work
done” (Lamport)"
©
2014
P.
Kuznetsov

18. Why theory of distributed computing?"
§ Every computing system is distributed"
§ Computing getting mission-critical"
ü Understanding fundamentals is crucial"
§ Intellectual challenge "
ü A distinct math domain?"
©
2014
P.
Kuznetsov

19. History"
§ Dining philosophers, mutual exclusion
(Dijkstra )~60’s"
§ Distributed computing, logical clocks (Lamport),
distributed transactions (Gray) ~70’s"
§ Consensus (Lynch) ~80’s"
§ Distributed programming models ~90’s"
§ Multicores, HTM now"
§ Principal conferences: PODC, DISC, SPAA,
ICDCS, STOC, FOCS, …"
©
2014
P.
Kuznetsov

20. Synchronization, blocking
and non-blocking
"

21. Producer-consumer (bounded buffer) problem
§ Producers put items in the buffer (of bounded size)"
§ Consumers get items from the buffer"
§ Every item is consumed, no item is consumed twice"
"(Client-server, multi-threaded web servers, pipes, …)"
Why synchronization? Items can get lost or consumed twice:"
"
Producer!
/* produce item */!
while (counter==MAX);!
buffer[in] = item !
in = (in+1) % MAX;!
counter++; !!
Consumer!
/* to consume item */!
while (counter==0); !
item=buffer[out];!
out=(out+1) % MAX;!
counter--; !
/* consume item */!
!
Race!
©
2014
P.
Kuznetsov

22. Synchronization tools
§ Semaphores (locks), monitors
§ Nonblocking synchronization
§ Transactional memory
©
2014
P.
Kuznetsov

23. Semaphores for producer-consumer
§ 2 semaphores used :"
ü empty: indicates empty slots in the buffer (to be used by the producer)"
ü full: indicates full slots in the buffer (to be read by the consumer)"
shared semaphores empty := MAX, full := 0;!
Producer" Consumer"
P(empty)!
buffer[in] = item; !
in = (in+1) % MAX;!
V(full)!
!
!
P(full);!
item = buffer[out];!
out=(out+1) % MAX; !
V(empty);!
©
2014
P.
Kuznetsov

24. Potential problems with semaphores/locks
§ Blocking: progress of a process is conditional (depends on other processes)"
§ Deadlock: no progress ever made!
"
!
§ Starvation: waiting in the waiting queue forever"
X1:=1; X2:=1!
Process 1! Process 2!
...!
P(X1)!
P(X2)!
critical section!
V(X2)!
V(X1)!
...!
...!
P(X2)!
P(X1)!
critical section!
V(X1)!
V(X2)!
...!
©
2014
P.
Kuznetsov

25. Non-blocking algorithms"
A process makes progress, regardless of the other processes"
shared buffer[MAX]:=empty; head:=0; tail:=0;"
Producer put(item)! Consumer get()!
if (tail-head == MAX){!
!return(full);!
}!
buffer[tail%MAX]=item; !
tail++;!
return(ok);!
if (tail-head == 0){!
!return(empty);!
}!
item=buffer[head%MAX]; !
head++;!
return(item);!
Problems: "
• works for 2 processes but hard to say why it works J"
• multiple producers/consumers? Other synchronization pbs?"
(highly non-trivial in general)"
©
2014
P.
Kuznetsov

26. Transactional memory"
§ Mark sequences of instructions as an atomic transaction, e.g., the resulting
producer code:"
atomic {!
!if (tail-head == MAX){!
!return full;!
!}!
!items[tail%MAX]=item; !
!tail++;!
}!
return ok;!
§ A transaction can be either committed or aborted!
ü Committed transactions are serializable !
ü + aborted/incomplete transactions are consistent (opacity/local serializability)!
ü Let the transactional memory (TM) care about the conflicts"
ü Easy to program, but performance may be problematic"
©
2014
P.
Kuznetsov

27. § Concurrency is indispensable in programming:"
ü Every system is now concurrent"
ü Every parallel program needs to synchronize"
ü Synchronization cost is high (“Amdahl’s Law”)"
§ Tools: "
ü Synchronization primitives (e.g., monitors, TAS, CAS, LL/SC)"
ü Synchronization libraries (e.g., java.util.concurrent)"
ü Transactional memory, also in hardware (Intel Haswell, IBM Blue Gene,…)"
§ Coming next:"
ü Characterization of implementability in shared-memory models"
" ©
2014
P.
Kuznetsov

28. Characterization of Distributed
Computing Models
"

29. t-­‐resilience
CAS
Locks
Transac>onal
memory
Message-­‐
passing
Shared-­‐
memory
Which features matter?"
Matter for what?"
Synchronization jungle"
Adversaries

30. A characterization?"
"
§ finding an equivalent (simpler) representation
of an object"
"
§ creating characters for a narrative"
ü Which characters matter? Equivalence results?"
©
2014
P.
Kuznetsov

31. A distributed computability play"
Characters: problems and models"
Intrigue: is P solvable in M? "
"
How many interesting plays are
there?"
""
§ Problems: objects (queues, stacks,
CAS), distributed tasks"
§ Models: message-passing,
shared-memory, wait-freedom, t-
resilience, adversaries"
J.L.Borges:"
there are only
four stories to tell"
©
2014
P.
Kuznetsov

32. Task solvability in read-write"
§ A task (I,O,Δ):"
ü Set of input vectors I"
ü Set of output vectors O"
ü Task specification Δ: I è 2O"
§ Consensus (universal task): "
ü Binary inputs and outputs"
ü Every output is an input (validity)"
ü All outputs are the same (agreement)"
"
"
©
2014
P.
Kuznetsov
Before
AHer
0
1
2
2
2
2

33. System model"
§ N asynchronous (no bounds on relative speeds)
processes p0,…,pN-1 (N≥2) communicate via read-
write shared memory"
§ Every process pi is assigned an algorithm Ai"
§ Processes can fail by crashing "
ü A crashed process takes only finitely many steps (reads
and writes)"
ü Up to t processes can crash: t-resilient system "
ü t=N-1: wait-free "
"
©
2014
P.
Kuznetsov

34. Solving a task"
"
§ A task T is solvable if for some distributed
algorithm {A0,…,AN-1} and every input vector I
in I:"
ü Every correct process eventually outputs a value
(decides)"
ü The output vector O is in Δ(I) "
©
2014
P.
Kuznetsov

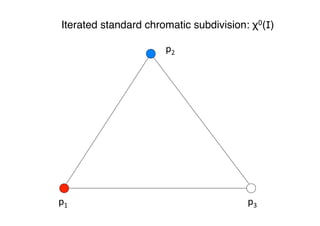
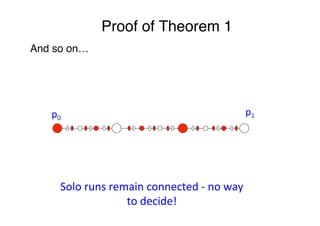
35. An easy story to tell"
"
Task solvability in the iterated immediate
snapshot (IIS) memory model "
§ Processes proceed in rounds"
§ Each round a new memory is accessed:"
ü Write the current state"
ü Get a snapshot of the memory "
ü Equivalent the standard (non-iterated) read-write
model [BGK14]"
§ Visualized via standard chromatic subdivision
χk(I) [BG97,Lin09,Koz14]"
©
2014
P.
Kuznetsov

36. Iterated standard chromatic subdivision: χ0(I)"
p1
p3
p2

37. χ1(I) : one round of IIS"
p1
p3
p2
p2
sees
{p1,p2}
p1
sees
{p1,p2}
p3
sees
{p1,p2,p3}
p2
sees
{p2,p3}
p3
sees
{p2,p3}

38. χ2(I) : two rounds of IIS"
p1
p3
p2

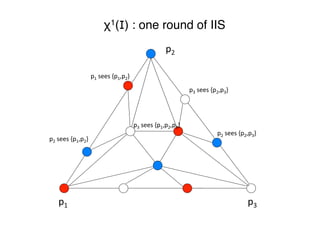
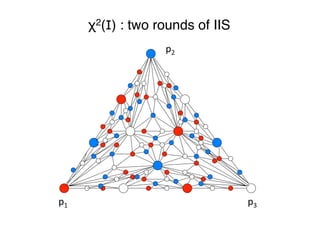
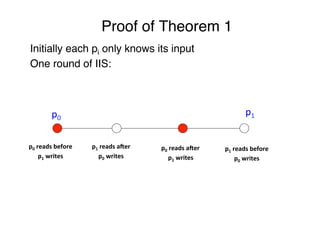
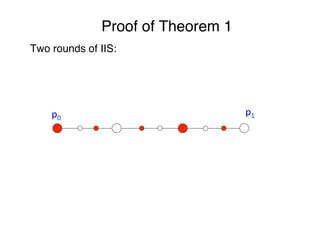
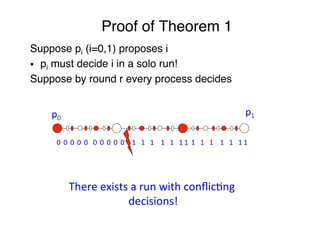
39. Impossibility of wait-free consensus [FLP85,LA87]"
Theorem 1 No wait-free algorithm solves consensus"
"
We give the proof for N=2, assuming that "
"p0 proposes 0 and p1 proposes 1"
"
"
Implies the claim for all N≥2"
"
©
2014
P.
Kuznetsov

40. Proof of Theorem 1"
p0
p1
p0
reads
before
p1
writes
p0
reads
a0er
p1
writes
p1
reads
a0er
p0
writes
p1
reads
before
p0
writes
Initially each pi only knows its input"
One round of IIS:"

41. Proof of Theorem 1"
p0
p1
Two rounds of IIS:"

42. Proof of Theorem 1"
p0
p1
And so on…"
Solo
runs
remain
connected
-­‐
no
way
to
decide!

43. Proof of Theorem 1"
p0
p1
Suppose pi (i=0,1) proposes i"
§ pi must decide i in a solo run!"
Suppose by round r every process decides"
"
There
exists
a
run
with
conflic>ng
decisions!
0
0
0
0
0
1
1
0
0
0
0
0
1
1
1
1
1
1
1
1
1
1
1
1

44. Thus"
§ Wait-free consensus is impossible (for all N)"
§ What about weaker forms of agreement?"
ü E.g., decide on at most k (k<N) different values:
k-set consensus"
ü k=N-1: set consensus"
"
Before
AHer
0
1
2
1
2
2

45. Impossibility of set consensus"
Theorem 2 No wait-free algorithm solves set
agreement in read-write"
"
§ Starting with N values, there is no way to drop one
(decide on at most N-1)"
"
§ Implies the impossibility of wait-free k-set consensus
for all k≤N-1"

46. Solving set consensus in IIS"
§ Each pi proposes its id i"
§ There is an IIS round r, such that each process
(that reaches round r) outputs some id "
§ In each run, the set of output ids is a subset of
participants of size ≤N-1"
"
Implies Sperner coloring of the subdivided simplex
IISr "

47. Sperner’s coloring of a subdivided simplex"
Each vertex of the original
simplex SN-1 (initial state) is
colored with a process id "
"
Each simplex in subdivision D is
contained in a face (subset) of
S and the union of simplexes
of D is S (|S|=|D|) "
"
Sperner’s coloring:"
"Each vertex v in the
subdivision D is colored with a
distinct color:"
ü If the vertex belongs to a face S of
SN-1, then d is in colors(S) "
"
P0
P1
P2
P0
P1
P2
SN-­‐1
D

48. Sperner’s Lemma"
Sperner coloring of any
subdivision D of SN-1 has a
simplex with all N colors"
"
"
"
"
Corollary: wait-free set
consensus is impossible in
IIS (and, thus, in read-write)"
P0
P1
P2

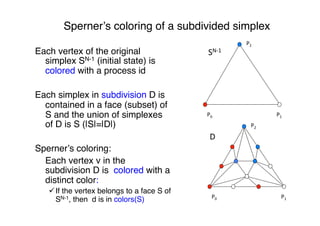
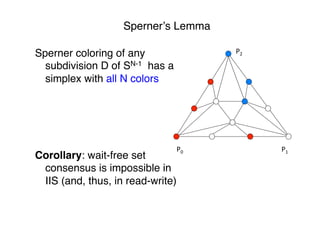
49. Characterization of wait-free task
solvability"
Asynchronous computability theorem[HS93]"
A task (I,O,Δ) is wait-free RW solvable if and
only if there is a chromatic simplicial map from a
subdivision χk(I) to O carried by Δ"
"
Wait-free task computability reduced to the
existence of continuous maps between
geometrical objects"
"
"

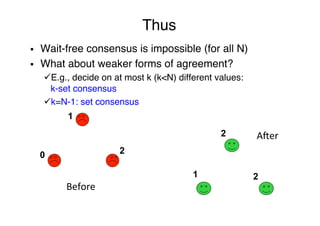
50. 1-resilient consensus?
k-resilient k-set agreement?""
"
NO"
"
Operational model equivalence:"
"
§ t-resilient N-process ó wait-free (t+1)-process
[BG93] (for colorless task, e.g. k-set agreement)"
"
[Main tool – protocol simulations]"
"

51. What about…"
§ Generic sub-models of RW"
ü Many problems cannot be solved
wait-free"
ü So restrictions (sub-models) of RW
were considered"
ü E.g., adversarial models [DFGT09]:
specifying the possible correct sets"
● Non-uniform/correlated fault probabilities"
● Hitting set of size 1: a leader can be
elected"
"
"

52. Beyond wait-free and colorless tasks "
§ A generic sub-IIS model is not
compact: does not contain limit
points "
§ A protocol cannot be a
approximated by a finite
subdivision: colors do matter "
©
2014
P.
Kuznetsov

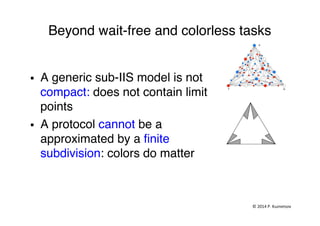
53. Terminating subdivisions [GKM14]"
A (possibly infinite) subdivision that
allows processes to stabilize (models
outputs): stable simplices stop
subdividing"
A terminating subdivision must be
compatible with the model: every run
eventually lands in a stable simplex "
©
2014
P.
Kuznetsov

54. Generalized asynchronous
computability theorem [GMK14]"
A task (I,O,Δ) is solvable in a sub-IIS model M if and
only if there exists a terminating subdivision T of I
(compatible with M) and a chromatic simplicial map
from stable simplices of T to O carried by Δ "
"
Topological characterization of every task facing
every (crash) adversary?"
What about stronger ones? What about
long-lived problems?"
"
"
©
2014
P.
Kuznetsov

55. Open problems"
§ Modeling and characterization"
ü Long-lived abstractions (queues, hash tables,
TMs…)"
ü Byzantine adversary: a faulty process deviates
arbitrarily"
ü Partial synchrony"
§ Complexity bounds"
ü Time (number of steps) and space (amount of
memory/communication)"
ü Optimal algorithm design"
§ Mathematics induced by DC"
ü filling the gap between the (too abstract)
algebraic/combinatorial topology and
algorithms"
"
©
2014
P.
Kuznetsov

56. ANR-DFG Cooperation 2014
Mathematical Methods in Distributed
Computing (DISCMAT)"
Partners:"
"
Petr Kuznetsov, Telecom ParisTech (coord.)"
Dmitry Kozlov, U Bremen"
Michel Raynal, U Rennes I"
"
"
"

57. References"
§ E. Gafni, P. Kuznetsov, C. Manolescu: A
generalized asynchronous computability
theorem. PODC 2014"
§ Z. Bouzid, E. Gafni, P. Kuznetsov: Strong
Equivalence Relations for Iterated Models.
OPODIS 2014"
§ M. Herlihy, S. Kozlov, S. Rajsbaum:
Distributed computing through combinatorial
topology. Morgan Kaufmann, 2014 "
§ More: http://perso.telecom-paristech.fr/
~kuznetso/ "
©
2014
P.
Kuznetsov

58. "
"
"
Спасибо!"
"