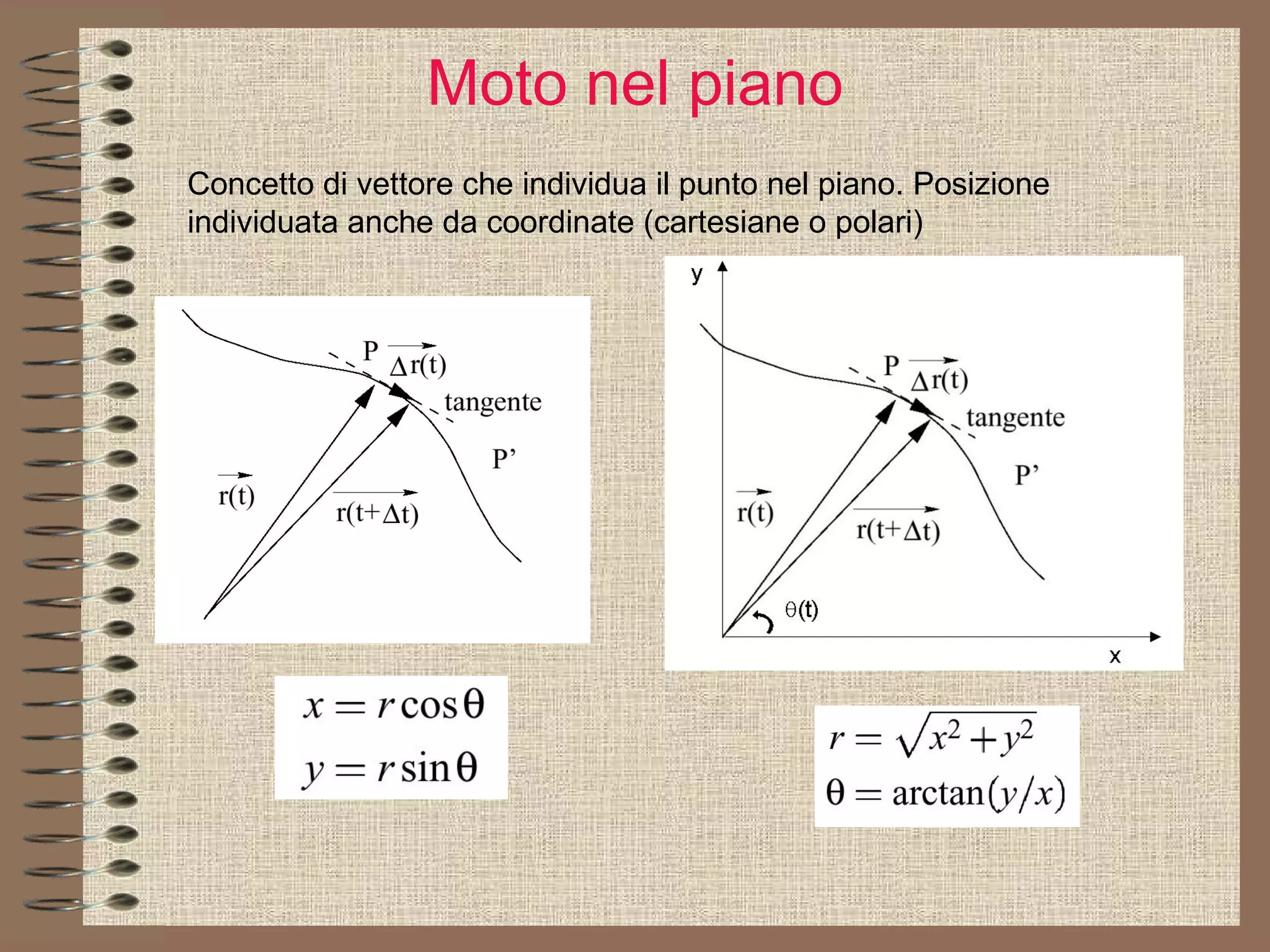
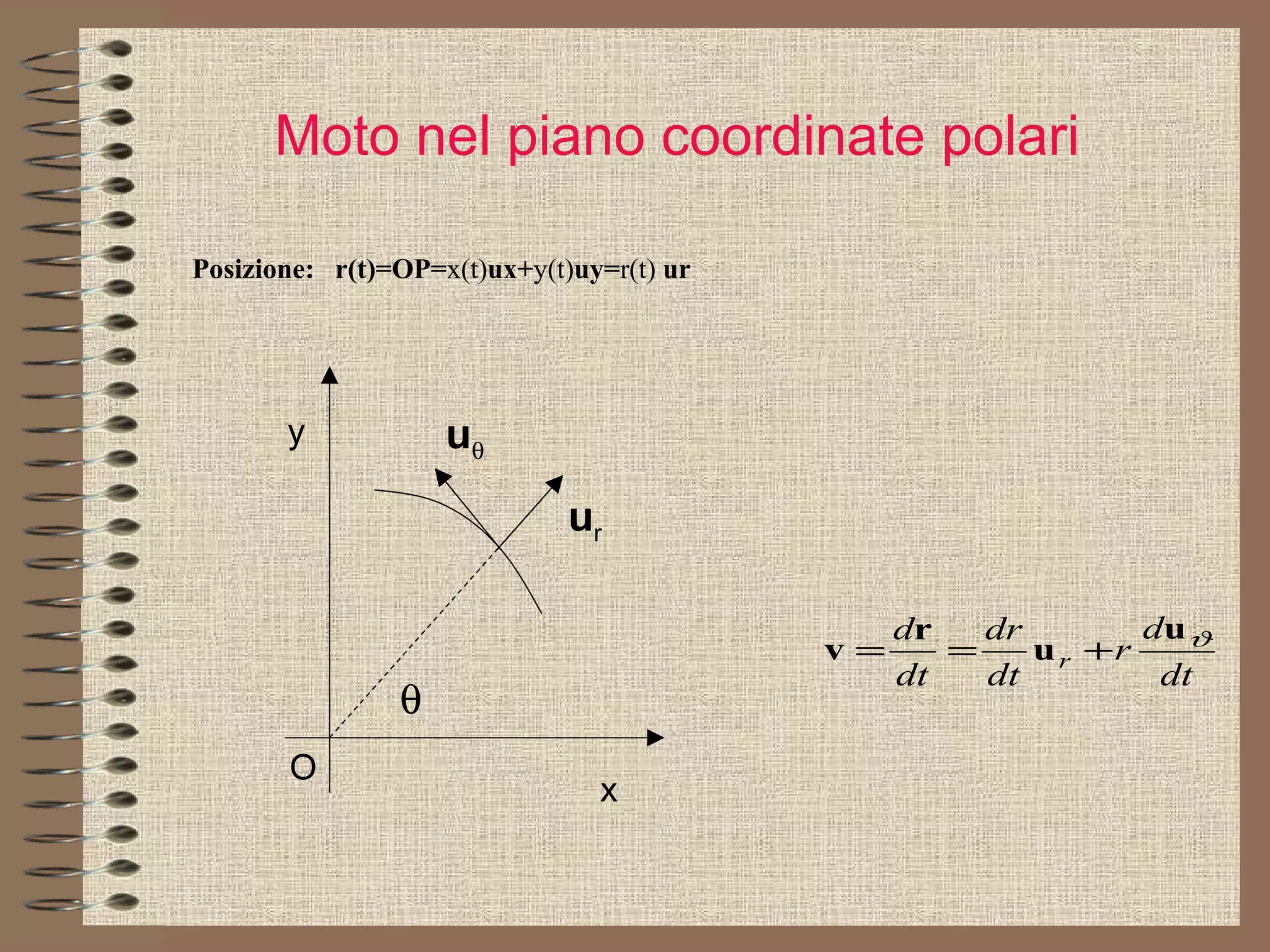
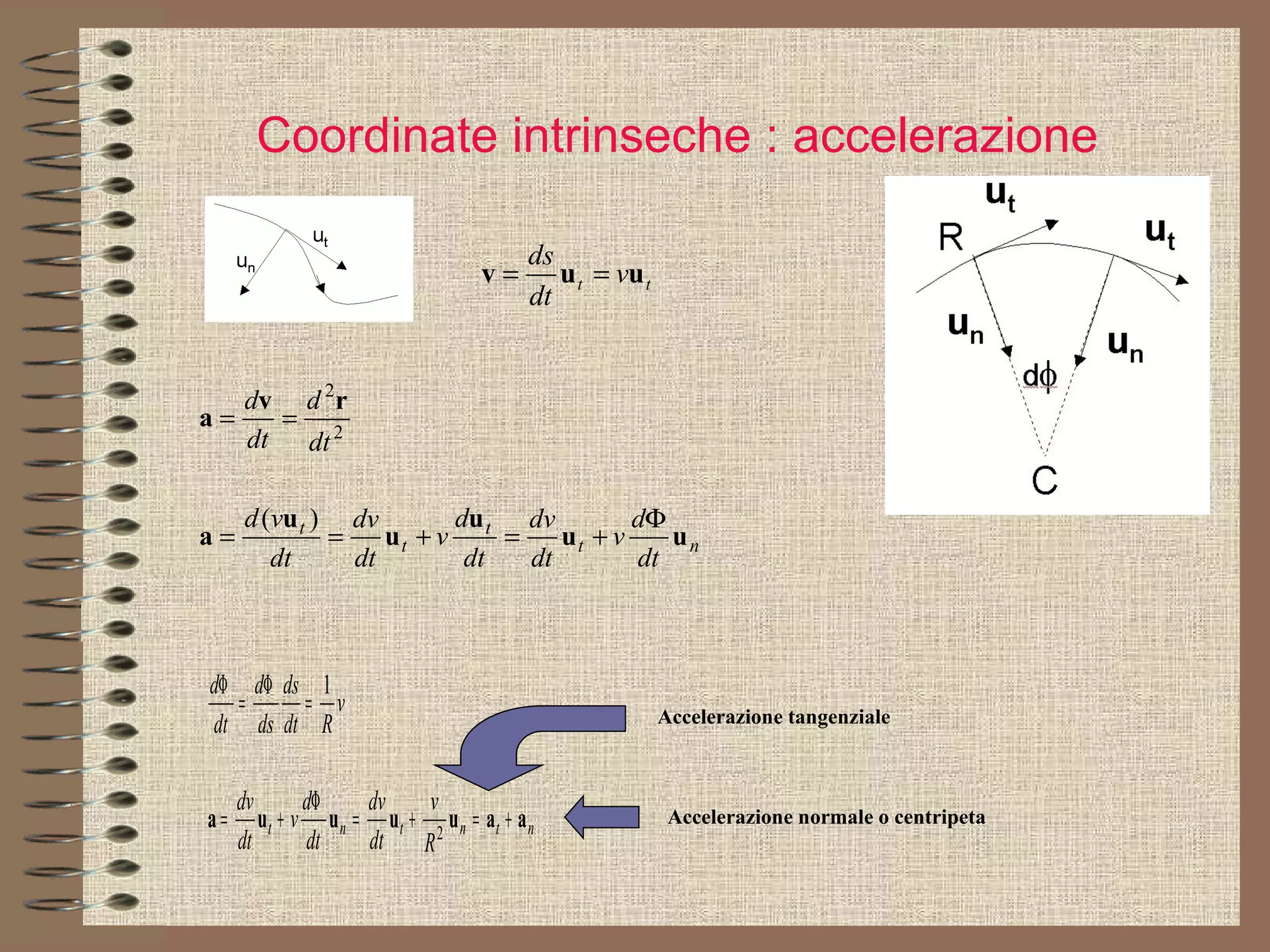
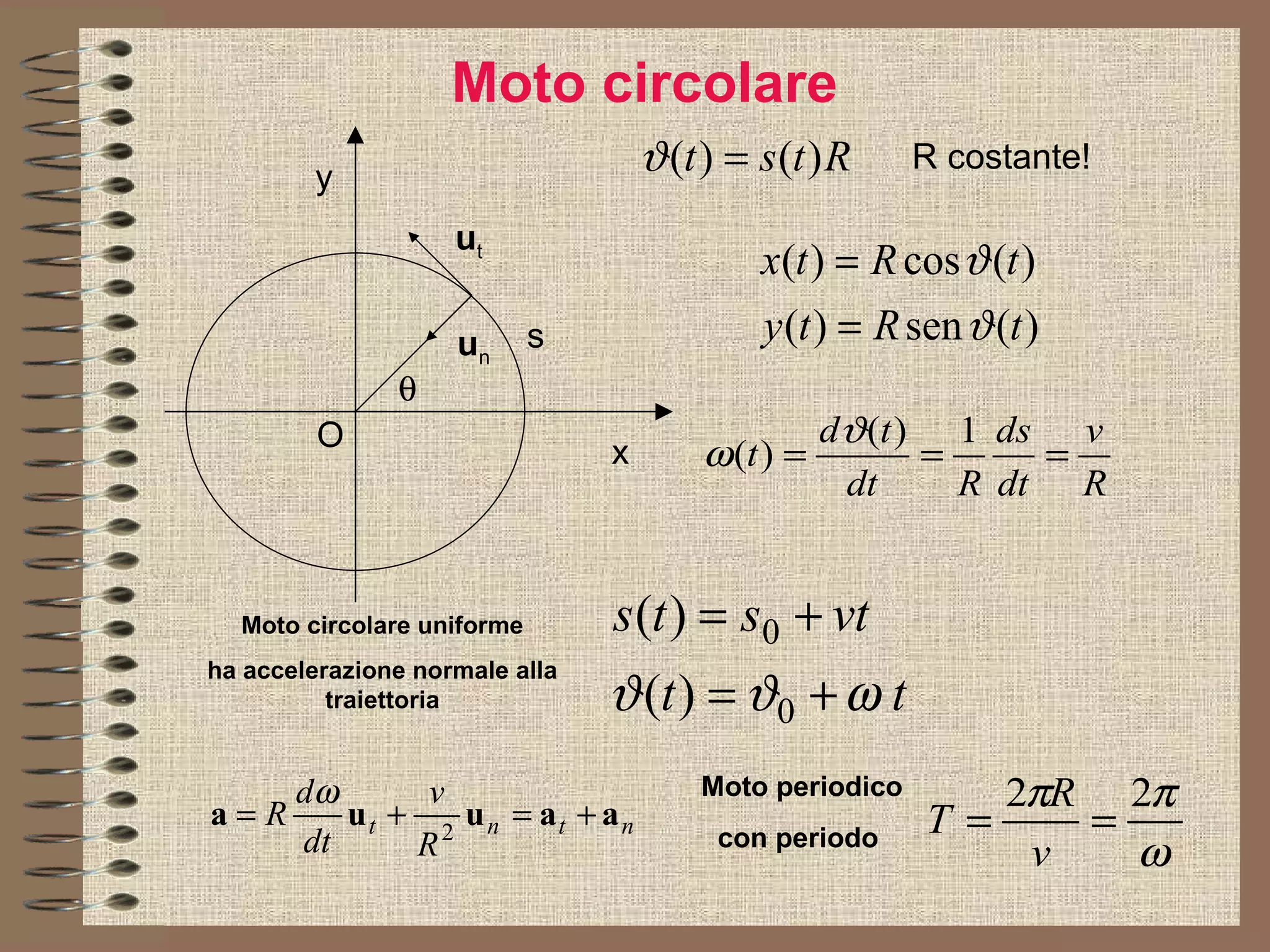
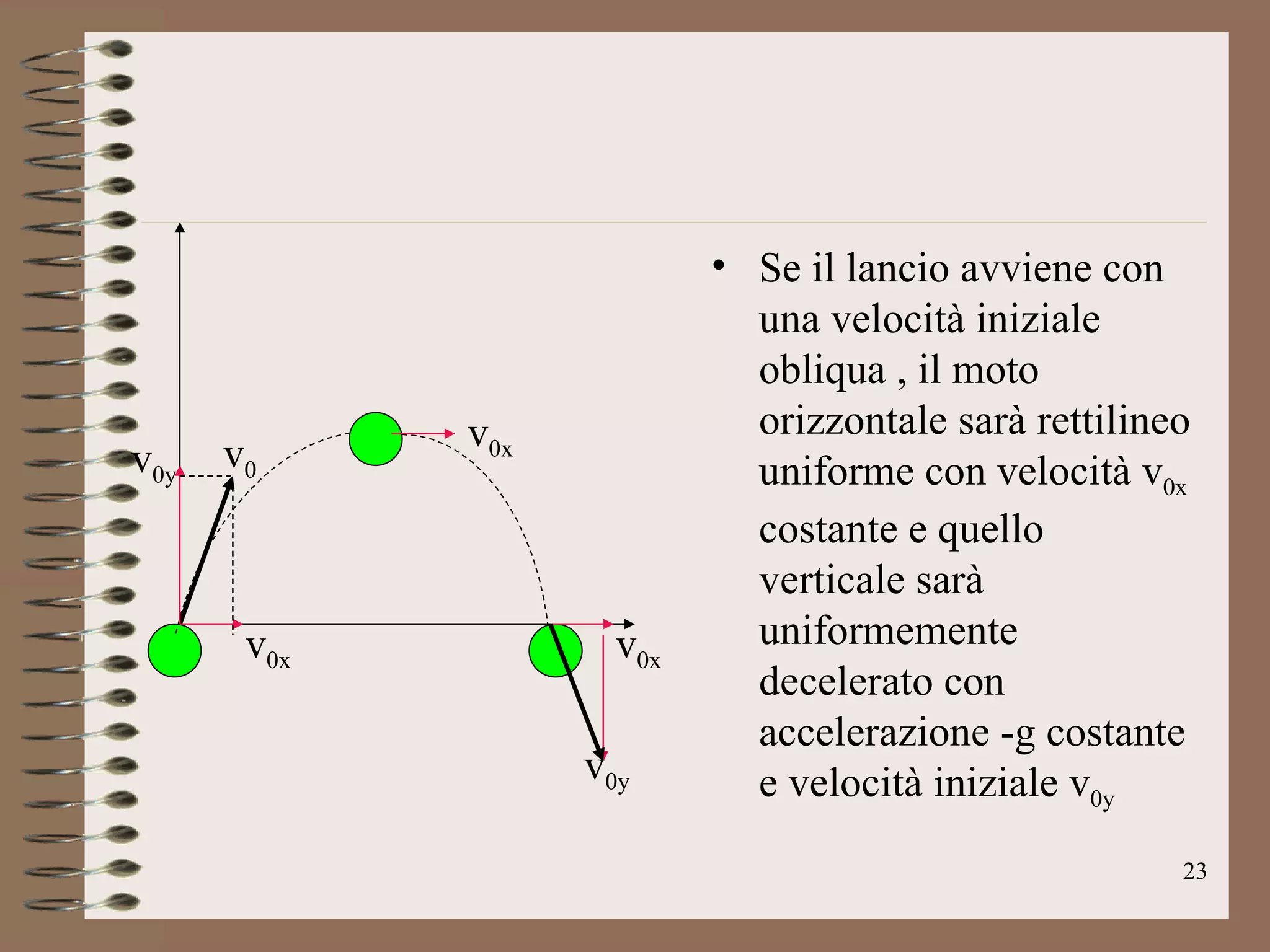
Il documento tratta delle coniche in fisica, concentrandosi sulla circonferenza e la parabola, che descrivono rispettivamente il moto circolare uniforme e il moto parabolico. Viene spiegato come le coniche siano generate dall'intersezione di un cono con un piano e si discute la loro rappresentazione tramite equazioni quadratiche. Infine, il documento analizza le applicazioni fisiche delle coniche, descrivendo il moto nel piano utilizzando sistemi di riferimento cartesiani e polari.

1. LE CONICHE IN FISICA SINTESI E APPUNTI

2. Introduzione alla geometria analitica Le coniche che vengono prese in considerazione in questo modulo sono la circonferenza e la parabola dato che descrivono in modo esaustivo il moto circolare uniforme e il moto parabolico di un grave. Si definisce conica quella curva che si ottiene intersecando un cono rotondo indefinito con un piano non passante per il vertice del cono. Consideriamo un cono rotondo indefinito di vertice V, asse k e sia a l'angolo formato dalla generatrice del cono con l'asse. Sia p un piano generico non passante per il vertice del cono, indichiamo con b l'angolo acuto che p forma con l'asse del cono.

3. Introduzione alla geometria analitica Tipi di sezioni coniche : i piani, intersecando il cono, descrivono una circonferenza ( in giallo ), un' ellisse ( in rosso ), una parabola ( in blu ) e un' iperbole ( in verde )

4. Le coniche in generale Le ellissi si ottengono intersecando il cono con piani che con il suo asse formano angoli maggiori di θ e minori o uguali a π/2; ciascuna di tali intersezioni appartiene ad una sola delle due falde del cono ed è una curva chiusa . Le circonferenze sono casi particolari di ellissi ottenute dalla intersezione del cono con un piano perpendicolare al suo asse. Il fatto di essere curve chiuse rende le ellissi e le circonferenze facilmente visualizzabili.

5. Le coniche in generale Il grafico di ogni equazione quadratica in due variabili reali, se i coefficienti soddisfano determinate condizioni che preciseremo, individua una sezione conica di un piano cartesiano, cioè di un piano riferito ad un sistema di coordinate cartesiane . Si trova inoltre che tutte le sezioni coniche si possono ottenere in questo modo. Se si considera l'equazione quadratica nella forma Si ha la seguente casistica: se 2 b = 4 ac , l'equazione rappresenta una parabola ; se 2 b < a c e a c e/o b 0, l'equazione determina una ellisse ; se a = c e b = 0, l'equazione esprime una circonferenza ; se 2 b > a c , l'equazione rappresenta una iperbole ; se a + c = 0, l'equazione rappresenta una iperbole rettangolare .

6. La circonferenza Circonferenza nel piano cartesiano In geometria analitica una circonferenza in un piano può essere descritta utilmente sia mediante le coordinate cartesiane, sia mediante le coordinate polari, sia in forma parametrica. In un sistema di assi cartesiani Oxy , la circonferenza di centro (α,β) e raggio r è il luogo dei punti caratterizzati dall'equazione: ( x − α) 2 + ( y − β) 2 = r 2 cioè è l'insieme di tutti e soli i punti che distano r da (α,β). All'equazione più generale si dà spesso la forma canonica: x 2 + y 2 + ax + by + c = 0,

7. La parabola In geometria analitica, il piano è dotato di coordinate cartesiane ortogonali, e una parabola può essere descritta come luogo di punti che soddisfa un'equazione di un certo tipo. Una parabola è l'insieme dei punti ( x , y ) del piano cartesiano che soddisfano una equazione quadratica del tipo dove:

8. Applicazione in fisica delle coniche Moto nel piano Descrizione del moto nel piano con coordinate cartesiane polari – intrinseche Moto circolare Moto parabolico

9. Sistemi di riferimento Il moto è relativo Ogni moto va studiato dopo avere fissato un sistema di riferimento, cioè un punto di vista da cui osservare il fenomeno. Un sistema di riferimento è rappresentato da una terna di assi cartesiani

10. Sistemi di riferimento In genere noi studiamo i fenomeni prendendo come sistema di riferimento la Terra

11. Moto nel piano Concetto di vettore che individua il punto nel piano. Posizione individuata anche da coordinate (cartesiane o polari)

12. Moto nel piano Vettore spostamento / Vettore posizione Posizione: r(t)=OP= x(t) ux+ y(t) uy Velocità istantanea Analogamente per l’accelerazione:

13. Moto nel piano coordinate cartesiane Posizione: r(t)=OP= x(t) ux+ y(t) uy

14. Moto nel piano coordinate polari Posizione: r(t)=OP= x(t) ux+ y(t) uy= r(t) ur x y O  u r u 

15. Coordinate intrinseche : accelerazione Accelerazione tangenziale Accelerazione normale o centripeta

16. LA VELOCITA’ La velocità è una grandezza vettoriale definita come rapporto tra spazio percorso e tempo impiegato a percorrerlo V = D s/D t = (s – s0)/(t – t0) Dove s0 è lo spazio percorso all’istante t0 ed s lo spazio percorso all’istante t. L’unità di misura nel S.I. è il m/s

17. Accelerazione L’ accelerazione è una grandezza vettoriale definita come la variazione di velocità in un certo intervallo di tempo a = Δ v/ Δ t (1) L’unità di misura è il m/s 2 Ricorda che: spostamento, velocità ed accelerazione hanno nel moto rettilineo la stessa direzione v s a

19. Moto circolare R costante! Moto circolare uniforme ha accelerazione normale alla traiettoria Moto periodico con periodo x y O u n u t  s

20. Che si può anche scrivere: v =2  r  Dove  è la frequenza La velocità angolare è definita come: Dove  è l’angolo spazzato dal raggio nel tempo t, quindi:

21. La velocità angolare è un vettore perpendicolare al piano della traiettoria e verso testa-punta di una vite destrorsa che si avvita nel verso del moto v =  r L’accelerazione centripeta, cioè diretta verso il centro del moto è data da: a c =   r =v 2 /r  v a c

22. MOTO PARABOLICO è la composizione di un moto rettilineo uniforme orizzontale e di un moto uniformemente accelerato verticale La sua equazione oraria è v 0

23. Se il lancio avviene con una velocità iniziale obliqua , il moto orizzontale sarà rettilineo uniforme con velocità v 0x costante e quello verticale sarà uniformemente decelerato con accelerazione -g costante e velocità iniziale v 0y v 0 v 0x v 0y v 0x v 0x v 0y

24. Se v x e v y sono le componenti della velocità in un generico istante t Le componenti dello spazio lungo gli assi saranno

25. Ricavando t dalla prima e sostituendo nella seconda si ottiene l’equazione oraria del moto Che rappresenta l’equazione di una parabola Ponendo y = 0 si ottiene la distanza tra il punto di lancio e quello di arrivo, cioè la gittata:

26. FINE