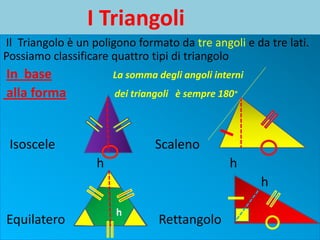
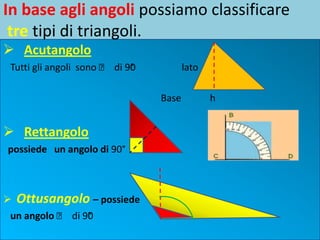
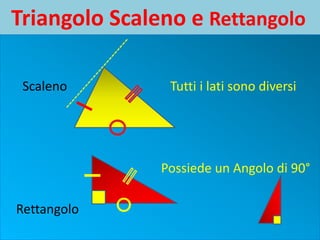
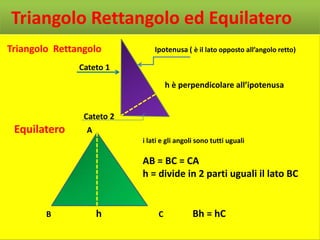
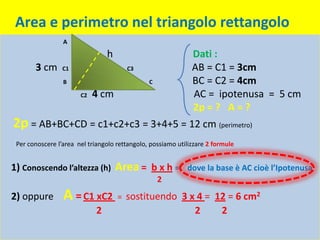
Il documento descrive le caratteristiche dei triangoli, classificandoli in base ai loro lati e angoli. Vengono presentate varie formule per calcolare il perimetro e l'area dei triangoli, inclusi triangoli isosceli, rettangoli ed equilateri. Inoltre, vengono esemplificati calcoli specifici per il perimetro e l'area di un triangolo rettangolo.

1. I Triangoli
Il Triangolo è un poligono formato da tre angoli e da tre lati.
Possiamo classificare quattro tipi di triangolo
In base La somma degli angoli interni
alla forma dei triangoli è sempre 180°
Isoscele Scaleno
h h
h
h
Equilatero Rettangolo

2. In base agli angoli possiamo classificare
tre tipi di triangoli.
 Acutangolo
Tutti gli angoli sono ˂ di 90
° lato
Base h
 Rettangolo
possiede un angolo di 90°
 Ottusangolo – possiede
un angolo ˂ di 90
°

3. Triangolo Scaleno e Rettangolo
Scaleno Tutti i lati sono diversi
Possiede un Angolo di 90°
Rettangolo

4. Triangolo Isoscele
C Caratteristiche: due lati
uguali e base diversa
Isoscele
L’altezza H divide la Base AB in due parti
uguali e divide anche il triangolo isoscele
in due triangoli rettangoli su cui
si potrà applicare il teorema di Pitagora.
A B Nel triangolo ACH
CH - diventa il cateto maggiore
AH = Cateto minore
H CA = Ipotenusa

5. Triangolo Rettangolo ed Equilatero
Triangolo Rettangolo Ipotenusa ( è il lato opposto all’angolo retto)
Cateto 1
h h è perpendicolare all’ipotenusa
Cateto 2
Equilatero A
i lati e gli angoli sono tutti uguali
AB = BC = CA
h = divide in 2 parti uguali il lato BC
B h C Bh = hC

6. Formule
• La lunghezza del perimetro è data dalla somma dei 3 lati
 2p = l1 + l2 + l3 l = lato
• Per misurare l’area occorre moltiplicare la base per l’altezza e
dividere il risultato per due
 A = b x h ( Formula Generale )
2
• Nel triangolo rettangolo possiamo utilizzare anche questa formula
 A = C1 x C2 dove C1= cateto maggiore
2 C2 = cateto minore e l’Ipotenusa

7. Il Triangolo – Applicazione Formule
 Perimetro
2p= l1+l2+l3 =
2p= AB+BC+CD
2p= 8+8+8 cm
 Area A= b x h Formula Generale
2
A= 8 x 6 = 48 = 24 cm2
2 2
Formule Inverse - (b = 2xA) (h= 2xA)
h b

8. Area e perimetro nel triangolo rettangolo
A
h Dati :
3 cm C1 C3 AB = C1 = 3cm
B C BC = C2 = 4cm
C2 4 cm AC = ipotenusa = 5 cm
2p = ? A = ?
2p = AB+BC+CD = c1+c2+c3 = 3+4+5 = 12 cm (perimetro)
Per conoscere l’area nel triangolo rettangolo, possiamo utilizzare 2 formule
1) Conoscendo l’altezza (h) Area = b x h = dove la base è AC cioè l’Ipotenusa
2
2) oppure A = C1 xC2 = sostituendo 3 x 4 = 12 = 6 cm2
2 2 2