Downloaded 13 times
Uploaded byKevin Adit
167618810 potensial-listrik
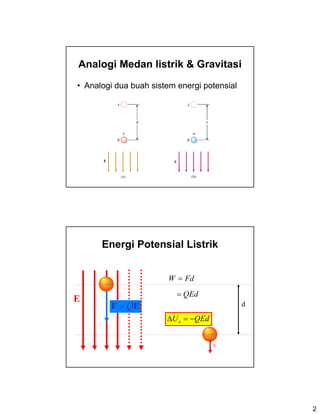
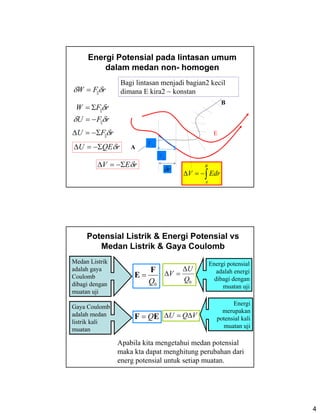
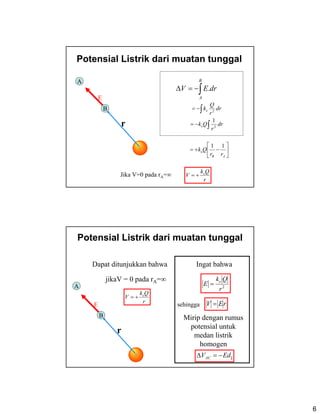
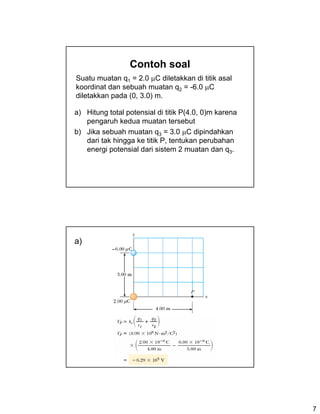
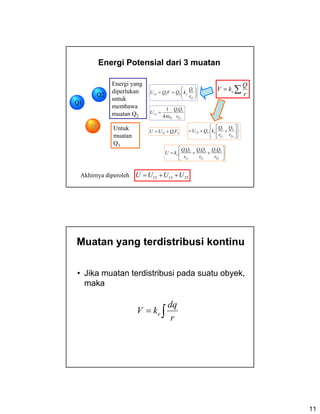
Dokumen ini membahas konsep usaha dalam konteks energi potensial listrik, dengan analogi antara medan listrik dan gravitasi. Energi potensial listrik dijelaskan melalui interaksi muatan dan penggunaan hukum Coulomb, serta persamaan untuk menghitung potensial dan energi dalam medan elektromagnetik. Terdapat juga contoh soal dan penjabaran tentang superposisi potensial dari beberapa muatan.
More Related Content
167618810 potensial-listrik
- 1. 1 Usaha • Anda melakukanusaha ketika mendorong benda ke atas pada suatu bidang miring (bukit) • Semakin tinggi bukit semakin banyak usaha yang anda lakukan: lintasan lebih panjang • Semakin curam/terjal bukit semakin banyak usaha yang anda lakukan : gaya lebih besar usaha adalah suatu produk dari gaya tetap yang bekerja pada benda sepanjang lintasan perpindahan. dFW ||= Energi Potensial Listrik
- 2. 2 Analogi Medan listrik& Gravitasi • Analogi dua buah sistem energi potensial Energi Potensial Listrik E EF Q= +Q +Q d FdW = QEd= QEdUe −=Δ v
- 3. 3 Energi Potensial Listrik •Kerja yang dilakukan (oleh medan listrik) pada partikel bermuatan adalah QEd • Partikel memperoleh tambahan Energi kinetik (QEd) • Oleh karena itu partikel harus telah kehilangan energi potensial sebesar ΔU=-QEd Potensial Listrik • Perubahan energi potensial adalah negatif kerja yang dilakukan oleh medan. sdEqWU B A∫ ⋅−=−=Δ 0 E A B sdE q U VVV B A AB ∫ ⋅−= Δ =Δ=− 0 1 V = 1 J/C 1 eV=1.6×10-19J
- 4. 4 Energi Potensial padalintasan umum dalam medan non- homogen rFW δδ ||= rFU δδ ||−= A B rFW δ||Σ= rFU δ||Σ−=Δ rQEU δΣ−=Δ rδ F|| rEV δΣ−=Δ ∫−=Δ B A EdrV Bagi lintasan menjadi bagian2 kecil dimana E kira2 ~ konstan E F⊥ Potensial Listrik & Energi Potensial vs Medan Listrik & Gaya Coulomb Apabila kita mengetahui medan potensial maka kta dapat menghitung perubahan dari energ potensial untuk setiap muatan. Gaya Coulomb adalah medan listrik kali muatan Medan Listrik adalah gaya Coulomb dibagi dengan muatan uji Energi potensial adalah energi dibagi dengan muatan uji Energi merupakan potensial kali muatan uji 0Q U V Δ =Δ 0Q F E = VQU Δ=ΔEF Q=
- 5. 5 Satuan Potensial (Tegangan)Listrik Satuan SI untuk potensial listrik 0Q U V Δ =Δ EdV −=Δ Satuannya adalah J/C Dikenal sebagai Volts (V) Telah ditunjukkan dVE /Δ= Karenanya E juga memiliki satuan V/m Beda Potensial dalam Medan Homogen E +Q +Q +Q A B C 0|| == dFWBC |||| QEddFWAB == BCABAC WWW += ||QEd= ||QEdUAC −=Δ d|| ||EdVAC −=Δ
- 6. 6 Potensial Listrik darimuatan tunggal + r ∫−=Δ B A drEV . ∫−= dr r Q ke 2 ∫−= dr r Qke 2 1 ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ −+= AB e rr Qk 11 Jika V=0 pada rA=∞ r Qk V e += E B A Potensial Listrik dari muatan tunggal + r jikaV = 0 pada rA=∞ r Qk V e += E B A Dapat ditunjukkan bahwa 2 r Qk E e = Ingat bahwa rEV =sehingga Mirip dengan rumus potensial untuk medan listrik homogen ||EdVAC −=Δ
- 7. 7 Contoh soal a) Hitungtotal potensial di titik P(4.0, 0)m karena pengaruh kedua muatan tersebut b) Jika sebuah muatan q3 = 3.0 μC dipindahkan dari tak hingga ke titik P, tentukan perubahan energi potensial dari sistem 2 muatan dan q3. Suatu muatan q1 = 2.0 μC diletakkan di titik asal koordinat dan sebuah muatan q2 = -6.0 μC diletakkan pada (0, 3.0) m. a)
- 8. 8 b) c) Contoh: Tegangan darisuatu Bola • Berapa potensial listrik antara permukaan sebuah bola dengan jejari 1m dengan sebuah titik A yang berjarak 0.5m dari permukaan apabila bola tersebut memiliki muatan sebesar +4μC? ++ + + + + + + + + + + + + + + A B
- 9. 9 Medan-medan yang berbeda •Medan serba-sama • Muatan titik • Jika lokasi awal (acuan) adalah tak hingga, maka dEV ⋅−=Δ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ −=− AB eAB rr qkVV 11 B e B r qk V = Potensial dari beberapa muatan Prinsip superposisi ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ ++= ... 2 2 1 1 r Q r Q kV e ∑= r Q kV e ...21 ++= VVV 1 1 1 r Q kV e= Total Potensial adalah jumlah seluruh potensial individual Potensial individual Total potensial adalah Dimana dapat dituliskan sebagai
- 10. 10 Superposisi Potensial Listrik •Dengan menggunakan titik acuan di tak hingga, kita dapat menghirung total tegangan/potensial dari banyak muatan • Perhatikan bahwa kita menjumlah secara skalar, bukan vektor. ∑= i i i e r q kV Contoh: Superposisi potensial • Dari gambar disamping, tentukan tegangan di titik pusat koordinat. Asumsikan tegangan sama dengan 0 di titik tak hingga. −3 mC +6 mC +6 mC
- 11. 11 Energi Potensial dari3 muatan ∑= r Q kV e Q2 Q1 Q3 ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ == 12 1 2212 r Q kQVQU e 12 21 0 12 4 1 r QQ U πε = 3312 VQUU += 231312 UUUU ++= ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ++= 23 32 13 31 12 21 r QQ r QQ r QQ kU e Energi yang diperlukan untuk membawa muatan Q2 Untuk muatan Q3 ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ++= 23 2 13 1 312 r Q r Q kQU e Akhirnya diperoleh Muatan yang terdistribusi kontinu • Jika muatan terdistribusi pada suatu obyek, maka ∫= r dq kV e
- 12. 12 Contoh: Potensial olehcincin bermuatan Sebuah elektron diletakkan pada jarak 5 m dari suatu sumbu cincin bermuatan yang terdistribusi secara homogen. Cincin memiliki jari-jari 0.03 m dan muatan persatuan panjang 3 mC/m. Tentukan laju elektron saat melewati loop cincin! r dq kdV e= ( ) 2 1 22 xR Q kV Q r k dQ r k V r dq kdV e ee e + = ==⇒= ∫∫∫ ( ) ( ) ( ) ( ) 2/322 2/3222/122 2 2 1 xR Qxk xxRQkxR dx d Qk dx dV E e eex + = +⎟ ⎠ ⎞ ⎜ ⎝ ⎛ −−=+−=−= −− ( ) 2/1 2 2/32 2 2 0 2 2 2 220 2 ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ + = =+= += x xRm Qek v x m eE x m qE v axvv e e e x e x Medan Ex dapat dihitung sebagai berikut Sehingga kecepatan elektron di sekitar x = 0 menjadi: Contoh: Potensial oleh cincin bermuatan (lanjutan)
- 13. 13 Mencari medan Edari potensial • Berapakah medan listrik pada (3m, 2m) untuk fungsi potensial berikut? • Dengan menentukan gradien (operasi nabla) terhadap fungsi potensial tsb. diperoleh • Sehingga untuk (3m, 2m) diperoleh 22 35),( yxyxyxV ++= jyxiyxyxE ˆ)65(ˆ)52(),( +−+−= CNjiE /27ˆ16)2,3( −−=