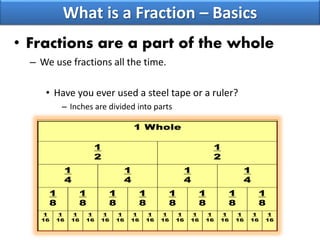
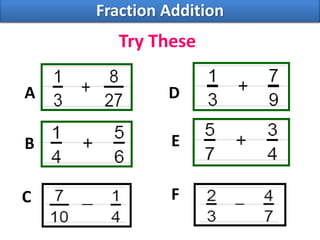
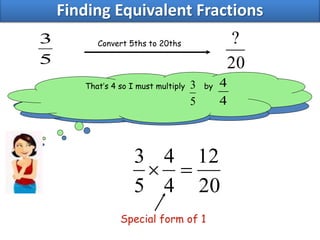
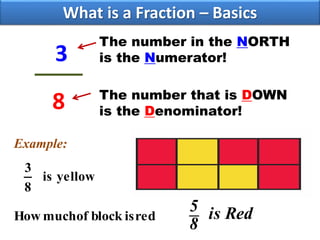
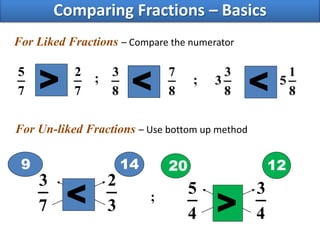
This document provides an overview of fractions including: - The basic components and types of fractions - How to perform operations like addition, subtraction, multiplication, and division of fractions - Converting between improper and mixed fractions - Finding equivalent and reduced fractions - Determining the lowest common denominator - Comparing fractions - The proper order of operations to solve equations with fractions

1. Fractions &
order
of
operations
By: Masoud Nassimi
1
Date: 02/10/2014

2. Fraction Basics
Types of Fractions
Division of Fractions
2
Multiplication of Fraction
Lowest Common Denominator
Addition Fraction
Subtraction of Fraction
Order of Operation

3. What is a Fraction – Basics
• Fractions are a part of the whole
– We use fractions all the time.
• Have you ever used a steel tape or a ruler?
– Inches are divided into parts

4. 3
8
The number in the NORTH
is the Numerator!
The number that is DOWN
is the Denominator!
What is a Fraction – Basics
Example:
yellowis
8
3
redisblockofmuchHow Redis
8
5

5. Types of Fractions – Basics
Proper Fractions – the numerator is SMALLER
than the denominator.
Improper Fractions – the numerator is LARGER
than the denominator.
Equivalent Fractions – are those which are
written with different numerator/denominator
pair, but the result is the same. (2)(12) = (3)(8)
Mixed Fractions – When a fraction is composed of
a whole number and a fraction.
Liked Fractions – When fractions have the same
denominators .
9
7
;
8
3
2
9
;
5
7
12
8
3
2

3
2
3
5
2
;
5
3

6. Mixed numbers to improper fractions

3
1
2
Convert whole numbers to thirds
3
1
2
3
7
3
16
3
1
3
6
3
1
2 


Mixed
number
Improper
fraction
Mixed Fractions – Basics

7. 2
1
32
31



An equivalent fraction is one that has the same value and
position on the number line but has a different denominator
Equivalent fractions can be found by multiplying
the denominator and numerator by the same
multiple that results to 1
1
5
5
4
4
3
3
2
2

Equivalent Fractions – Basics
6
3

4
1
34
31



12
3
;

8. Examples:
?equalandIs
45
30
21
14
21
14 reduce 


721
714
45
30 reduce
9
6
545
530


 reduce 


39
36
Now we know that these two
fractions are actually the same!
Equivalent Fractions – Basics
3
2
3
2
MultiplycrosscanweAlso 45
30
21
14
 30214514 
630630 
? ?

9. 2
2
6
6
7
7
8
8
9
9
10
10
11
11
17
17
25
25
20
20
50
50
125
125
Multiplying by one
• Multiplying any
number by 1
does not
change the
value 4x1=4,
9x1=9 …

10. Simplifying means finding an equivalent fraction with the
LOWEST denominator by making a special form of 1
equal to 1
18
12
6
6
3
2
 1
3
2

3
2

18
12
618
612



3
2

Another way
of doing this
Simplifying Fractions / Reducing – Basics

11. Comparing Fractions – Basics
For Un-liked Fractions – Use bottom up method
8
7
8
3
For Liked Fractions – Compare the numerator
14
< 8
1
5
8
3
3
<7
2
7
5
> ;
;
;
3
2
7
3
9 12
> 4
3
4
5
20
<

12. Example:
Comparing Fractions – Basics
Janet got 10 out of 15 for her test and
Tom got 15 out of 20. Ann said they
both did equally well because they both
got 5 wrong. Is Ann correct?
20
15
15
10
225
<
200
NO
Tom got higher
score
Janet Tom

13. 5
3
20
?Convert 5ths to 20ths
What do we multiply 5 by to get a product of
20?
That’s 4 so I must multiply by
4
4
5
3
20
12
4
4
5
3

Special form of 1
Finding Equivalent Fractions

14. Finding LCD for { 4 , 5 , 9 , 12 , 6 , 20 }
Finding Lowest Common Denominator
The Lowest Common Denominator / Multiple (LCD/LCM)
is the smallest common multiple of two or more numbers.
1) First eliminate the denominator(s) that are already a factor of another
denominator such as 4 ; 5 ; & 6 are factors of 20 & 12.
2) List the denominators left (9, 12, 20) as
shown on the table. Start with a lowest
prime number that is divisible by at least
two numbers with no remainder.
If a number is not divisible, then write the
original number back.
3) Repeat the process until there is one on
each column. LCD is the product of
numbers on the first column
9 12 20
2 9 6 10
2 9 3 5
3 3 1 5
3 1 1 5
5 1 1 1
LCD = 2  2  3 x 3  5 = 180

15. Fraction Multiplication
Numerator times Numerator
Denominator time Denominatorbd
ac
d
c
b
a 
7
4
5
3 
Examples:
72
25;



36
35
5
4
36
35
315
312
13
7
1
2
236
535
55
24 




36
35
15
12 
35
12
8
5
9
5 
13
11
13
14 

16. Fraction Division
bc
ad
c
d
b
a
d
c
b
a 
Examples:
515
555
25
18
15
55
25
18

55
15
25
18 
125
66
The first (left) fraction stays
as is, the second fraction is
reciprocated & the sign
changes from division to
multiplication. Multiply as
explained previous slide
315
11
25
318
3
11
25
18



5
11
25
6

17. Fraction Addition and Subtraction
 The objects must be of the same type, i.e. we combine
bundles with bundles and sticks with sticks.
 In fractions, we can only combine pieces of the same
size. In other words, the denominators must be the
same (Like Fraction). Then add/Subtract the numerators
 If Denominators are different (Unlike Fractions), then we
must first find its equivalents, so all fractions have the
same denominator. Then add / subtract numerators

18. Addition of Fractions with equal denominators
+ = ?Example:
8
3
8
1 
Fraction Addition
Like Fractions
+ =
The answer is
8
3)(1 
2
1
8
4 
88
31

 This is NOT the right answer
because the denominators
cannot be added

19. Addition of Fractions with different denominators
+ = ?Example:
Fraction Addition
Unlike Fractions
5
2
3
1

In this case, we need to first convert them into
equivalent fraction with the same denominator.
15
5
53
51
3
1




15
6
35
32
5
2




An easy choice for a common
denominator is 3×5 = 15
Therefore, 
15
6
15
5
5
2
3
1
15
11

20. Subtraction of Fractions with different denominators
Example:
Fraction Subtraction
Unlike Fractions
5
2
3
2 
In this case, we need to first convert them into
equivalent fraction with the same denominator.
15
10
53
52
3
2 


15
6
35
32
5
2




An easy choice for a common
denominator is 3×5 = 15
Therefore, 
15
610
15
6
15
10
5
2
3
2
15
4

21. This is more difficult than before, so please take notes.
2
1
1
4
1
3 
Easy way to solve mixed numbers is to first convert them into
improper fraction and then perform subtraction/addition
2
121
4
143
2
1
1
4
1
3




2
3
4
13

4
6
4
13

4
3
1
4
7

Fraction Subtraction
2
3
4
13

2
2


22. Try These
A
F
EB
C
D
Fraction Addition

23. Answers On Next Slide
• Each click on the next slide
reveals an answer.
• Check your papers.
• If you discover an incorrect
answer, be able to explain your
mistake.
Fraction Addition

24. Try These
A
F
EB
C
D
17
27
10
9
41
28
13
12
Fraction Addition
2
21
9
20

25. Remember the phrase
“Please Excuse My Dear Aunt Sally” or
PEMDAS.
1. Parentheses - ( ) or [ ]
2. Exponents or Powers
3. Multiply and Divide (from left to right)
4. Add and Subtract (from left to right)
Order of Operation

26. 20 - 3 • 6 + 102 + (6 + 1) • 4
= 20 - 3 • 6 + 102 + (7) • 4 (parentheses)
= 20 - 3 • 6 + 100 + (7) • 4 (exponents)
= 20 - 18 + 100 + 28 (Multiply l/r.)
= 2 + 100 + 28 (Subtract l/r.)
= 130 (Add.)
Order of Operation
Example

27. Which of the following represents
112 + 18 - 33 · (4 + 1) in simplified form?
1. -3,236
2. 4
3. 107
4. 16,996
Answer Now
Order of Operation

28. The
End
28