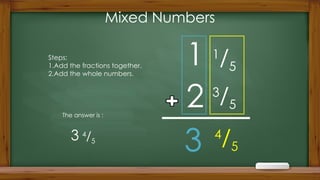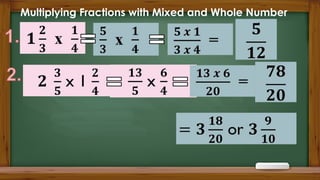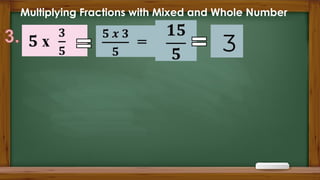The document provides a comprehensive guide on performing arithmetic operations on rational numbers, specifically focusing on addition and subtraction of both like and unlike fractions, as well as operations involving mixed numbers. It outlines step-by-step procedures for simplifying fractions and includes various activities for practice. Additionally, it explains multiplication and division of fractions, emphasizing the importance of simplification and cancellation.

3. 1. Perform operations on rational numbers:
Addition and subtraction of similar/like
fractions.

4. Adding and
Subtracting Like/
Similar Fractions
By: Maren Miller

5. Review
• What is a numerator?
• What is a denominator?
• What does a normal fraction look like?
• What does an improper fraction look like?
• What does a mixed number look like?

6. Review

7. Review

8. Review

9. Review

11. Like Fractions
When fractions have the same
denominator, they are like or similar
fractions.
You can add or subtract fractions when
you have similar fractions.
These are all like or similar fractions.
4 7 6 3 2 5
5 5 5 5 5 5

12. Adding Similar Fractions
Steps:
1. Make sure that you have like fractions.
2. Add the numerators.
3. Write the sum over the denominator.
4. Write the answer in simplest form.
1
6
4
6
5
6
The answer is:
5
6

13. Adding Similar Fractions
Steps:
1. Make sure that you have like fractions.
2. Add the numerators.
3. Write the sum over the denominator.
4. Write the answer in simplest form.
2
3
7
3
7
3
The answer is:
7
3

14. Adding Similar Fractions
Steps:
1. Make sure that you have like fractions.
2. Add the numerators.
3. Write the sum over the denominator.
4. Write the answer in simplest form.
7
9
4
9
11
9
The answer is:
11
9

15. Subtracting Similar Fractions
Steps:
1. Make sure that you have like fractions.
2. Subtract the numerators.
3. Write the difference over the denominator.
4. Write the answer in simplest form.
7
8
3
8
4
8
The answer is:
1
2

16. Subtracting Similar Fractions
Steps:
1. Make sure that you have like fractions.
2. Subtract the numerators.
3. Write the difference over the denominator.
4. Write the answer in simplest form.
4
7
3
7
1
7
The answer is:
1
7

17. Subtracting Similar Fractions
Steps:
1. Make sure that you have like fractions.
2. Subtract the numerators.
3. Write the difference over the denominator.
4. Write the answer in simplest form.
2
3
1
3
1
3
The answer is:
1
3

18. Mixed Numbers
There are two ways to change mixed numbers so you can
add or subtract.
• Change the mixed number into an improper fraction.
• Change just the fraction and leave the whole number
alone.

19. Mixed Numbers
1 1
/5
2 3
/5
Steps:
1.Add the fractions together.
2.Add the whole numbers.
4
/5
3
The answer is :
3 4
/5

20. Example: Add or subtract, write in simplest form.
1. 1 3
/8 - 11
/8 =
2. 2 2
/5 + 1 1
/5 =
3. 1 7
/8 – 1 6
/8 =
4. 3 4
/7 + 2 3
/7 =
1
/4
3 3
/5
1
/8
6
2 7
/9

21. ACTIVITY 1: Add or subtract, then simplify.
1.1
/5 + 2
/5 =
2. 2
/3 - 1
/3 =
3. 3
/4 + 2
/4 =
5
/4 or 1 1
/4
3
/5
1
/3

22. ACTIVITY 1: Add or subtract, then simplify.
8
/9
or 1 1
/7
8
/7
2
/2 = 1
4. 5
/7 + 3
/7 =
5. 3
/2 - 1
/2 =
6. 3
/9 + 5
/9 =

23. ACTIVITY 1: Add or subtract, then simplify.
7. 2
/8 - 2
/8 =
8. 4
/5 - 3
/5 =
9. 12
/4 - 3
/4 =
10. 2
/6 + 3
/6=
0
5
/6
1
/5
9
/4
or
2 1
/4

24. Activity 2: Answer the ff. and write your conclusion.
2
14
5
14
7
14
The answer
is:
1
2

25. Activity 2: Answer the ff. and write your conclusion.
20
24
10
24
10
24
The answer
is:
5
12

27. 1. Perform operations on rational numbers:
Addition and subtraction of unlike or
dissimilar fractions.

33. Unlike Fractions
Unlike fractions have different denominators.
Adding or subtracting with unlike fractions
isn’t that different from adding or
subtracting like fractions. You just have to
find what their denominators have in
common.
2
3
5
6
5
8
3
4
These are all unlike or dissimilar fractions.

34. Changing Unlike to Like
2
3
4
6
Steps:
1.Find a common multiple that will go into both denominators.
2.Multiply the numerator and denominator by the same number so the
denominator is the same as the common multiple.
WHAT EVER YOU DO TO THE BOTTOM YOU HAVE TO DO TO THE TOP!
3, 6, 9
2
3
5
15
Now you’re ready to
use these fractions
for addition and
subtraction!
2
2
2, 4, 6
3
6
19
6

35. Changing Unlike to Like
3
6
21
42
Steps:
1.Find a common multiple that will go into both denominators.
2.Multiply the numerator and denominator by the same number so the
denominator is the same as the common multiple.
WHAT EVER YOU DO TO THE BOTTOM YOU HAVE TO DO TO THE TOP!
6,12,18,24,30,36,42
7
6
2
12
7
7
7,14, 21,28,35,42
6
42
33
42

36. Changing Unlike to Like
8
12
64
96
Steps:
1.Find a common multiple that will go into both denominators.
2.Multiply the numerator and denominator by the same number so the
denominator is the same as the common multiple.
WHAT EVER YOU DO TO THE BOTTOM YOU HAVE TO DO TO THE TOP!
8,16,24,32,40,48,56,64
72,80,88,96
8
12
5
60
8
8 12, 24,36,48,60,72,84,96
12
96
4
96

37. Changing Unlike to Like
8
9
56
63
Steps:
1.Find a common multiple that will go into both denominators.
2.Multiply the numerator and denominator by the same number so the
denominator is the same as the common multiple.
WHAT EVER YOU DO TO THE BOTTOM YOU HAVE TO DO TO THE TOP!
7,14,21,28,35,42,49,56,63
7
9
4
36
7
7 9,18,27,36,45,54,63
9
63
20
63

38. Activity #1 Add fractions, put them in simplest form
1. 1
/2 + 1
/3 = 2. )
1
/3 + 1
/5 =
3.) 5
/6 + 1
/3 = 4.)
1
/8 + 3
/4 =
5.) 3
/3 + 5
/6 =
5
/6
8
/15
7
/8
1 5
/6
1 1
/6

39. Activity #2 Subtract fractions, put them in simplest form
1.1
/5 - 2
/5 = 2.)
1
/4 - 1
/6 =
3.) 7
/8 - 2
/3 = 4.)
4
/5 - 3
/10 =
1
/10
1
/12
5
/24
1
/2
5
/9

40. Activity 3: Answer the ff. and write your conclusion.
1. Nomi swam four-fifths of a lap in the morning and
seven-fifteenths of a lap in the evening. How much
farther did Nomi swim in the morning than in the
evening?
4
5
7
15
12-7
15
5
15
1
3

41. Activity 3: Answer the ff. and write your conclusion.
2. It took Gabriel five-thirds of an hour to complete his math
homework on Monday, three-fourths of an hour on Tuesday,
and five-sixths of an hour on Wednesday. How many hours did
he take to complete his homework altogether?
5
3
3
4
20+9+10
12
39
12
5
6

43. 1. Perform operations on rational numbers:
Multiplying fractions.

45. Multiplying Fractions
Multiply the numerator by numerator and
multiply the denominator by denominator.
Simplify if possible.
5
6
18
25
90
150
3
5
Or we may use the other way,
multiplying fractions using cancellation.

46. Multiplying fractions using cancellation
Look to simplify before multiplying.

47. Multiplying Fractions By Cancelling Common Factors
Look to simplify before multiplying.
9
16
10
21
90
336
45
168
15
56

48. Multiplying Fractions By Cancelling Common Factors
Look to simplify before multiplying.
14
15
15
16
210
240
7
8

49. Multiplying Fractions with Mixed and Whole Number

50. Multiplying Fractions with Mixed and Whole Number

51. Activity 1: Multiply the ff. fractions.
2
15
7
10
1
3
1
3
1
63

52. Activity 2: Multiply the fractions. Use canceling when
possible.
11
8
6

53. Activity 3: Solve the ff. problem.
1. A student can eat 1/8 of a pizza. If
there are 40 students in Sherill's class,
how many pizzas does Sherill need ?

54. Activity 3: Solve the ff. problem.
There are 50 lions.

56. 1. Perform operations on rational numbers:
Multiplying fractions.

58. Dividing Fractions
Change the division symbol as multiplication and take
the reciprocal of the second fraction and multiply
the numerator by numerator and multiply the
denominator by denominator. Simplify if possible.

59. Dividing Fractions
Change the division symbol as multiplication and take
the reciprocal of the second fraction and multiply
the numerator by numerator and multiply the
denominator by denominator. Simplify if possible.

60. Dividing Fractions
Change the division symbol as multiplication and take
the reciprocal of the second fraction and multiply
the numerator by numerator and multiply the
denominator by denominator. Simplify if possible.

61. Activity 1: Divide the ff. fractions.

62. Activity 2: Solve the ff. problem.
1. A piece of wire is 2/5 m long. If it is cut
into 8 pieces of equal length, how long will
each piece be?

63. Activity 2: Solve the ff. problem.
2. How many halves are there in six-
fourths?
Therefore, there are 3 halves in six-fourths.