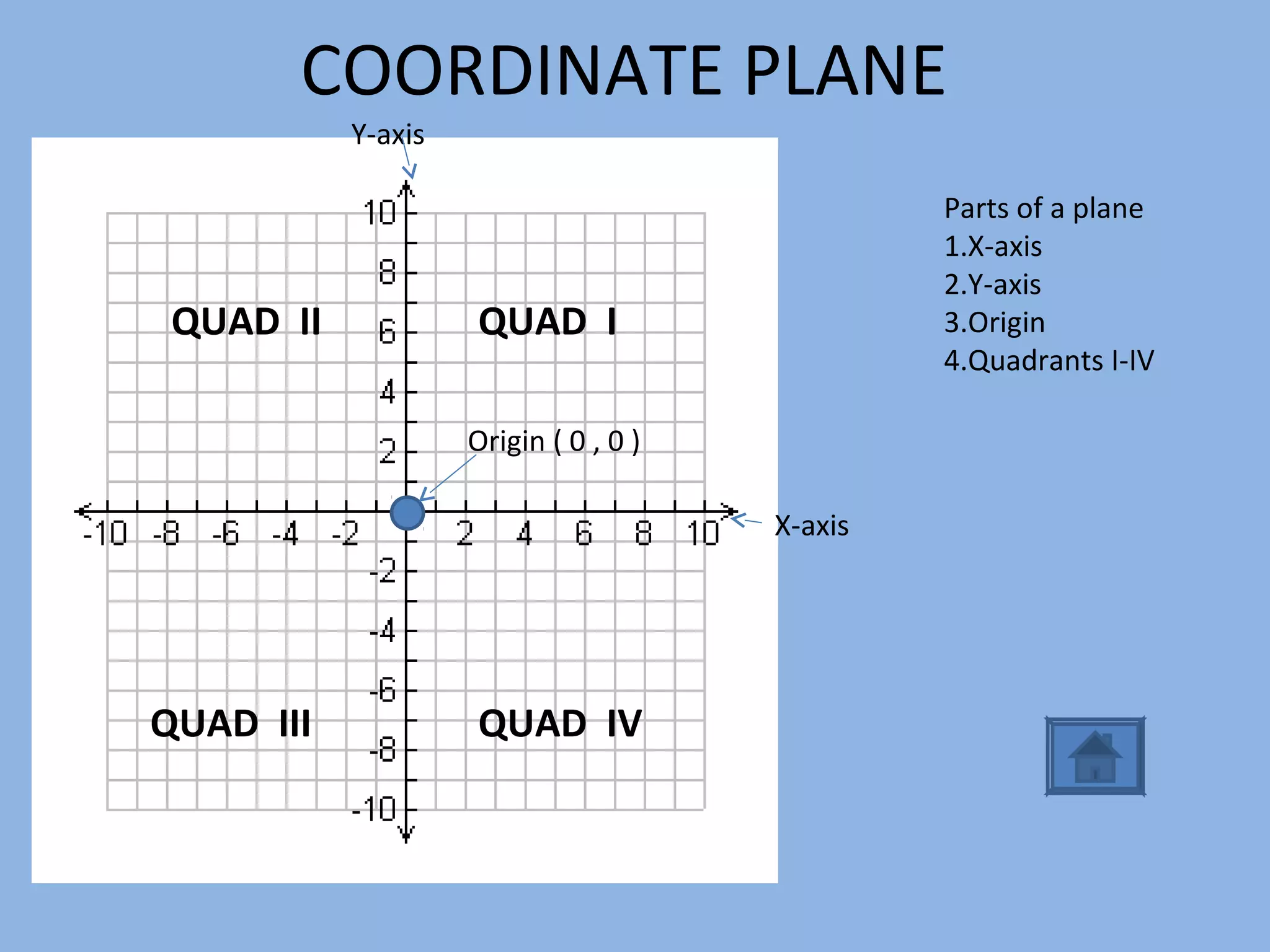
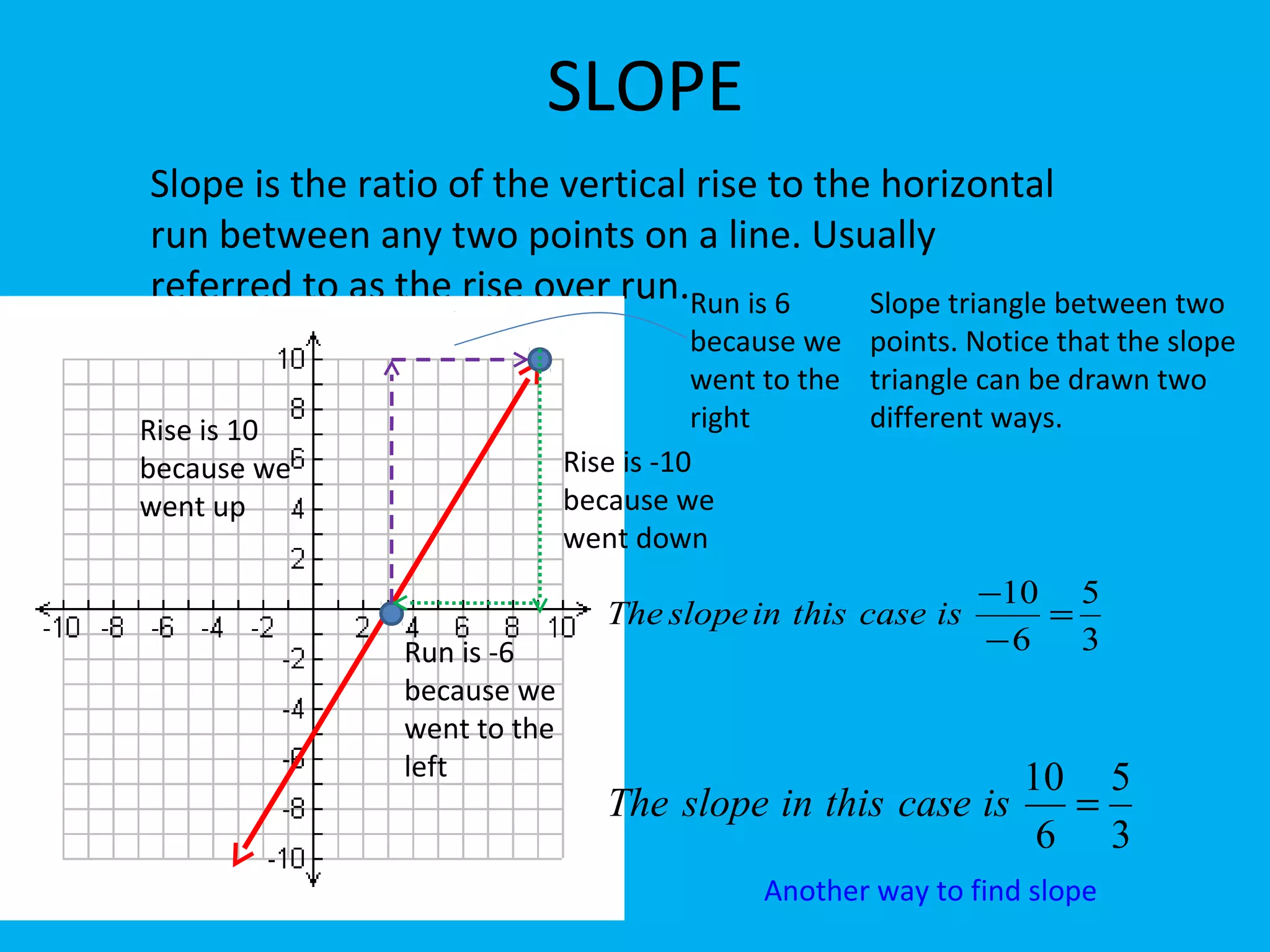
The document covers fundamental concepts related to linear equations, including plotting points, calculating slopes, identifying x and y intercepts, and using slope-intercept form to graph lines. It provides formulas for finding slopes between points and instructions for converting equations to slope-intercept form, as well as methods for graphing lines. Additionally, it includes a variety of assignments for practice on these topics.

1. LINEAR EQUATIONS PART I
1. Basic Coordinate Plane Info
2. Review on Plotting Points
3. Finding Slopes
4. x and y intercepts
5. Slope-Intercept Form of a Line
6. Graphing Lines
7. Determine the equation of a line given two points, slope an
Assignments

2. COORDINATE PLANE
Parts of a plane
1.X-axis
2.Y-axis
3.Origin
4.Quadrants I-IV
X-axis
Y-axis
Origin ( 0 , 0 )
QUAD IQUAD II
QUAD III QUAD IV

3. PLOTTING POINTS
Remember when plotting
points you always start at
the origin. Next you go left
(if x-coordinate is negative)
or right (if x-coordinate is
positive. Then you go up (if
y-coordinate is positive) or
down (if y-coordinate is
negative)
Plot these 4 points
A (3, -4), B (5, 6), C (-4, 5)
and D (-7, -5)
A
B
C
D

4. SLOPE
Slope is the ratio of the vertical rise to the horizontal
run between any two points on a line. Usually
referred to as the rise over run. Slope triangle between two
points. Notice that the slope
triangle can be drawn two
different ways.
Rise is -10
because we
went down
Run is -6
because we
went to the
left
3
5
6
10
=
−
−
iscasethisinslopeThe
Rise is 10
because we
went up
Run is 6
because we
went to the
right
3
5
6
10
=iscasethisinslopeThe
Another way to find slope

5. FORMULA FOR FINDING SLOPE
21
21
12
12
YY
XX
YY
XX
RUN
RISE
SLOPE
−
−
=
−
−
==
The formula is used when you know
two points of a line.
),(),( 2211 YXBandYXAlikelookThey
EXAMPLE

6. Find the slope of the line between the two points (-4, 8) and (10, -4)
If it helps label the points. 1X 1Y
2X 2Y
Then use the
formula
12
12
YY
XX
−
−
)8()4(
)4()10(
−−
−−
FORMULAINTOSUBSTITUTE
6
7
12
14
)8(4
410
)8()4(
)4()10(
−=
−
=
−+−
+
=
−−
−−
SimplifyThen

7. X AND Y INTERCEPTS
The x-intercept is the x-coordinate of a point
where the graph crosses the x-axis.
The y-intercept is the y-coordinate of a point
where the graph crosses the y-axis.
The x-intercept would be 4 and is
located at the point (4, 0).
The y-intercept is 3 and is
located at the point (0, 3).

8. SLOPE-INTERCEPT FORM OF A LINE
The slope intercept form of a line is y = mx + b, where
“m” represents the slope of the line and “b”
represents the y-intercept.
When an equation is in slope-intercept form the
“y” is always on one side by itself. It can not be
more than one y either.
If a line is not in slope-intercept form, then we must
solve for “y” to get it there.
Examples

9. IN SLOPE-INTERCEPT NOT IN SLOPE-INTERCEPT
y = 3x – 5 y – x = 10
y = -2x + 10 2y – 8 = 6x
y = -.5x – 2 y + 4 = 2x
Put y – x = 10 into slope-intercept form
Add x to both sides and would get y = x + 10
Put 2y – 8 = 6x into slope-intercept form.
Add 8 to both sides then divide by 2 and would get y = 3x + 4
Put y + 4 = 2x into slope-intercept form.
Subtract 4 from both sides and would get y = 2x – 4.

10. GRAPHING LINES
BY MAKING A TABLE OR USING THE
SLOPE-INTERCEPT FORM
I could refer to the table method by input-output table or x-y table. For now I
want you to include three values in your table. A negative number, zero, and a
positive number.
Graph y = 3x + 2
INPUT (X) OUTPUT (Y)
-2 -4
0 2
1 5
By making a table it gives me three points, in this case (-2, -4) (0, 2) and (1, 5) to plot
and draw the line.
See the graph.

11. Plot (-2, -4), (0, 2) and (1, 5)
Then draw the line. Make sure your
line covers the graph and has
arrows on both ends. Be sure to
use a ruler.
Slope-intercept graphing

12. Slope-intercept graphing
Steps
1.Make sure the equation is in slope-intercept form.
2.Identify the slope and y-intercept.
3.Plot the y-intercept.
4.From the y-intercept use the slope to get another point to draw the line.
1. y = 3x + 2
2. Slope = 3 (note that this means the
fraction or rise over run could be (3/1)
or (-3/-1). The y-intercept is 2.
3. Plot (0, 2)
4. From the y-intercept, we are going
rise 3 and run 1 since the slope was
3/1.

13. FIND EQUATION OF A LINE GIVEN 2
POINTS
1. Find the slope between the two
points.
2. Plug in the slope in the slope-
intercept form.
3. Pick one of the given points and plug
in numbers for x and y.
4. Solve and find b.
5. Rewrite final form.
Find the equation of the line between (2, 5) and (-2, -3).
1. Slope is 2.
2. y = 2x + b
3. Picked (2, 5) so
(5) = 2(2) + b
4. b = 1
5. y = 2x + 1
Two other ways

14. Steps if given the slope and
a point on the line.
1.Substitute the slope into
the slope-intercept form.
2.Use the point to plug in
for x and y.
3.Find b.
4.Rewrite equation.
If given a graph there are three
ways.
One way is to find two points on
the line and use the first method
we talked about.
Another would be to find the
slope and pick a point and use the
second method.
The third method would be to find
the slope and y-intercept and plug
it directly into y = mx + b.

15. Assignments
Pages 206-208 #’s 1-31, 33-39
Pages 233-235 #’s 10-21, 23-36, 43, 44
Pages 272-275 #'s 4-39, 54-73
Pages 282-283 #’s 20-34, 49-51
Pages 213-215 #'s 3-48
Pages 219-221 #’s 1-32, 35-42
Pages 225-227 #'s 18-32, 39-47
Pages 246-249 #'s 3-48, 67-78
Pages 288-290 #'s 3-35, 41-48