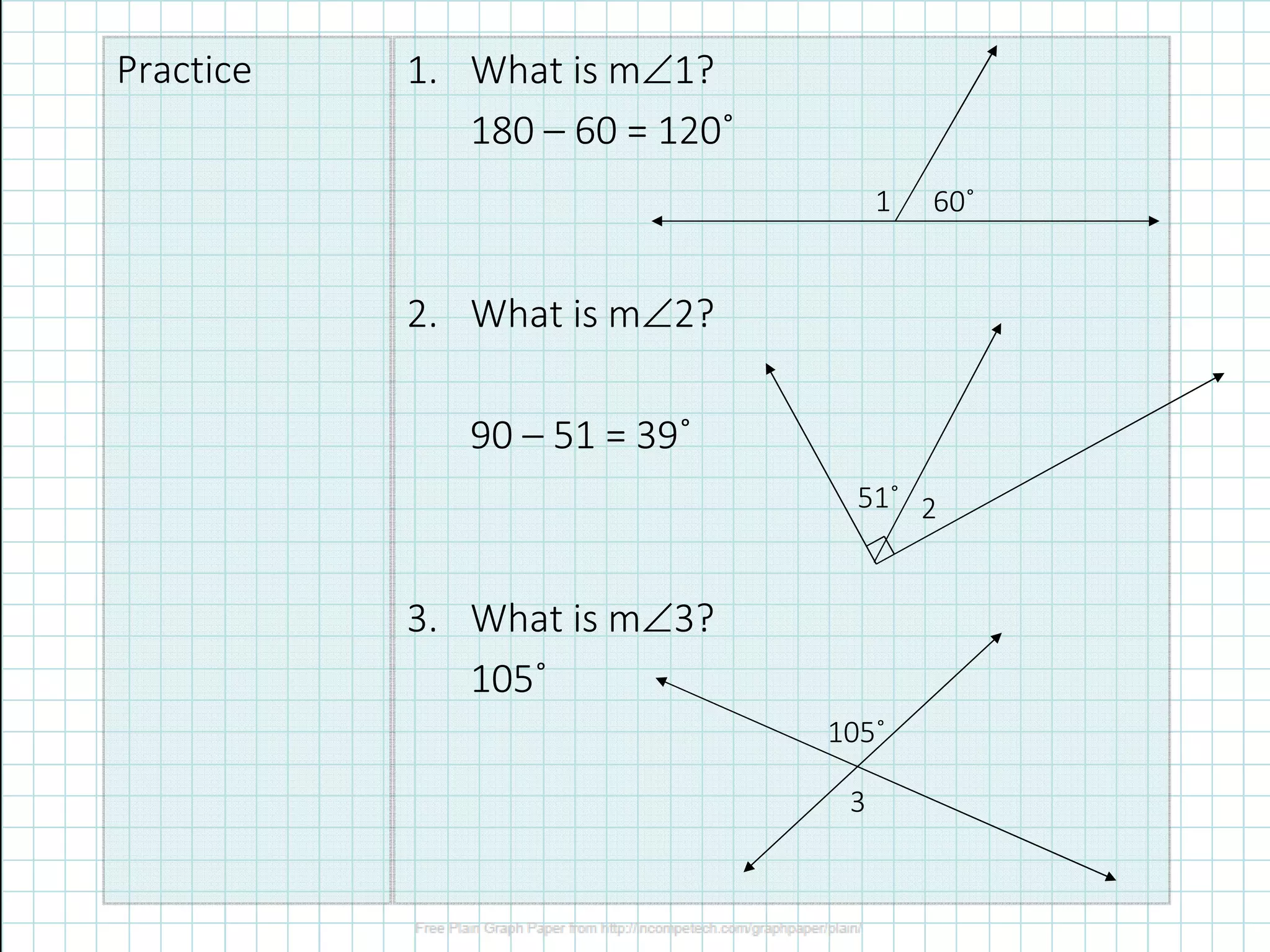
The document outlines the objectives for students to identify and use relationships between different types of angles including linear pairs, vertical angles, complementary angles, and supplementary angles. It provides definitions and examples for adjacent angles, linear pairs, vertical angles, complementary angles (sum of 90°), and supplementary angles (sum of 180°). Additionally, there are practice problems for students to determine the measures of specific angles.

1. Pairs of Angles
Objectives:
The student will be able to (I can):
Identify
• linear pairs
• vertical angles
• complementary angles
• supplementary angles
and use these relationships to set up and solve equations.

2. adjacent anglesadjacent anglesadjacent anglesadjacent angles – two angles in the same plane with a
common vertex and a common side, but no common
interior points.
Example:
∠1 and ∠2 are adjacent angles.
linear pairlinear pairlinear pairlinear pair – two adjacent angles whose noncommon sides
are opposite rays. (They form a line.)
Example:
1
2

3. vertical anglesvertical anglesvertical anglesvertical angles – two nonadjacent angles formed by two
intersecting lines. They are always congruent.They are always congruent.They are always congruent.They are always congruent.
Example:
∠1 and ∠4 are vertical angles
∠2 and ∠3 are vertical angles
1
2
3
4

4. complementary anglescomplementary anglescomplementary anglescomplementary angles – two angles whose measures have
the sum of 90°.
supplementary anglessupplementary anglessupplementary anglessupplementary angles – two angles whose measures have the
sum of 180°.
∠A and ∠B are complementary. (55+35)
∠A and ∠C are supplementary. (55+125)
A
55°
B
35°
C
125°

5. Practice 1. What is m∠1?
2. What is m∠2?
3. What is m∠3?
1 60˚
51˚ 2
105˚
3

6. Practice 1. What is m∠1?
180 – 60 = 120˚
2. What is m∠2?
90 – 51 = 39˚
3. What is m∠3?
105˚
1 60˚
51˚ 2
105˚
3