アルゴリズムとデータ構造11

アルゴリズムとデータ構
造
１１．「整列アルゴリズ
ム II 」2011 年 4 月 27 日（水）
服部　健太

2011/4/27 アルゴリズムとデータ構造 11 2
概要
 より効率的な整列手法である，クイックソー
ト，ヒープソート，マージソートについて説
明する
 それらの計算量についても議論する
 優先順位キューについて説明し，ヒープによ
る実現方法を示す
 基数ソートの概要を説明する

クイックソート
 平均， O(n log n) の高速なアルゴリズム
 ただし，最悪の場合， O(n2
) かかる
 1960 年に C.A.R. ホーアが発明
 Elliot803 という計算機向けに，シェルソートのラ
イブラリルーチンを実装しているときに思いつい
たらしい
 分割統治（ Divide and Conquer ）という考
え方にもとづく

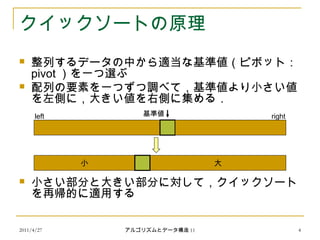
クイックソートの原理
 整列するデータの中から適当な基準値（ピボット：
pivot ）を一つ選ぶ
 配列の要素を一つずつ調べて，基準値より小さい値
を左側に，大きい値を右側に集める．
 小さい部分と大きい部分に対して，クイックソート
を再帰的に適用する
小大
基準値left right

クイックソートの素朴な実現
def quick_sort(A, left, right):
if left < right:
p = partition(A, left, right)
quick_sort(A, left, p – 1)
quick_sort(A, p + 1, right)
def partition(A, left, right):
pivot = A[right]
p = left - 1
for i in range(left, right):
if A[i] <= pivot:
p = p + 1; swap(A, p, i)
swap(A, p + 1, right)
return p + 1
2 8 7 1 3 5 6 4
left right
↑i↑p
2 8 7 1 3 5 6 4
↑i↑p
2 8 7 1 3 5 6 4
↑i↑p
2 8 7 1 3 5 6 4
↑i↑p
2 1 7 8 3 5 6 4
↑i↑p
2 1 3 8 7 5 6 4
↑i↑p
2 1 3 8 7 5 6 4
↑i↑p
2 1 3 87 5 64
↑i↑p

クイックソートの計算量
 最悪の計算量
 ピボットとして常に，最大，または，最小のものが選択さ
れる
 一方が n-1 ，もう一方が空の組に分割される
 O(N2
)
 最良の計算量
 ピボットとして常に中央の値が選択される
 半分ずつに分割される
 O(NlogN)
 平均的な計算量
 O(NlogN)

ヒープソート
 以下の形のコードで表せる
 for i in range(n-1, 0, -1):
 A[1], …, A[i] のうち最大値を求めそれを A[p] と
する
 A[i] と A[p] を入れ換える
 選択法の改良
 単純な選択法では，線形探索によって最大値（最
小値）を求めた
 最大値をすばやく求めることができれば，たとえ
ば， logN の計算量で最大値を取り出せれば，全
体の計算量は NlogN となる

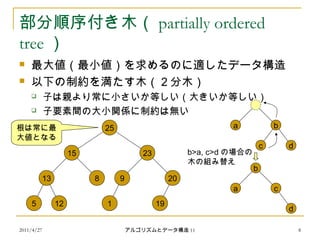
部分順序付き木（ partially ordered
tree ）
 最大値（最小値）を求めるのに適したデータ構造
 以下の制約を満たす木（２分木）
 子は親より常に小さいか等しい（大きいか等しい）
 子要素間の大小関係に制約は無い
25
15 23
13 8 9
5 12 1
根は常に最
大値となる
19
20
a b
c d
b
a c
d
b>a, c>d の場合の
木の組み替え

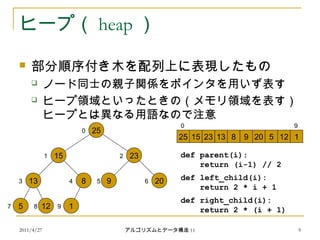
ヒープ（ heap ）
 部分順序付き木を配列上に表現したもの
 ノード同士の親子関係をポインタを用いず表す
 ヒープ領域といったときの（メモリ領域を表す）
ヒープとは異なる用語なので注意
25
15 23
13 9
5 12
20
25 15 23 13 8 9 20
1
8
5 12 1
0 9
0
1 2
3 4 5 6
7 8 9
def parent(i):
return (i-1) // 2
def left_child(i):
return 2 * i + 1
def right_child(i):
return 2 * (i + 1)

ヒープからの最大値の取り出し
25
15 23
13 9
5 12
20
1
8
15 1
13 9
5 12
208
23
15 23
13 9
5 12
208
1
15 20
13 9
5 12
18
23
（１）配列の最後の要素を先頭に持ってくる
　　　　 A[0] = A[heap_size-1]
　　　　 heap_size =heap_size - 1
（２）ヒープを正しく組み替える
　　大きい方の子と交換

ヒープの組み替え
 入力：配列 A ，インデックス i
 left_child(i) と right_child(i) はそれぞれヒープ
 A[i] は，子より小さいかもしれない
 ヒープ条件が満たされていないかもしれない
def max_heapify_down(A, i, heap_size):
l = left_child(i)
r = right_child(i)
if l < heap_size and A[l] ＞ A[i]:
largest = l
else:
largest = i
if r < heap_size and A[r] ＞ A[largest]:
largest = r
if largest != i:
swap(A, i, largest)
max_heapify_down(A, largest, heap_size)
heap_size はヒープ
の要素数を保持する
ものとする

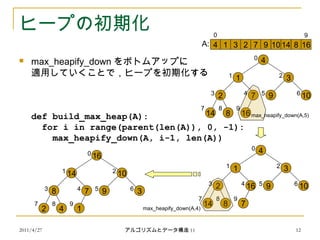
ヒープの初期化
 max_heapify_down をボトムアップに
適用していくことで，ヒープを初期化する
def build_max_heap(A):
for i in range(parent(len(A)), 0, -1):
max_heapify_down(A, i-1, len(A))
1 3
2 9
14 8
10
4
16
7
4 1 3 2 7 9 1014 8 16A:
0
1 2
3 4 5 6
7 8 9
90
max_heapify_down(A,5)
14 10
8 9
2 4
3
16
1
7
0
1 2
3 4 5 6
7 8 9
1 3
2 9
14 8
10
4
7
16
0
1 2
3 4 5 6
7 8 9

ヒープソートの実現
 以下の処理を繰返し，大きい方の値から順次
確定していく
 ヒープから最大値を取り出して，ヒープ
の大きさを１減らし，ヒープを再構成す
る
 ヒープの大きさを減らすとき， A[i] の場所
があくので，取り出した最大値をそこに
置くのがポイント
def heap_sort(A):
heap_size = len(A)
build_max_heap(A)
for i in range(len(A)-1, 0, -1):
swap(A, i, 0)
heap_size = heap_size – 1
max_heapfy_down(A, 0, heap_size)
14 10
8 9
2 4
3
16
1
7
0
1 2
3 4 5 6
7 8 9
14
108
9
2
4 3
161
7
0
1 2
3 4 5 6
7 8
swap(A,1,10)
heap_size を 1 減らす

ヒープソートの計算量
 ヒープの作成： O(N)
 max_heapify_down(A,i) で調べる段数
 最大値を取り出す部分： O(N log N)
 したがって， O(N log N)
 平均的には，クイックソートの 2 倍くらい遅い
     
   
)1(21)1(2)2(2221
2
1)1(log8/24/12/0
24/18/
12/14/012/
32
+−=×−+×−++×+×
=
×−++×+×+×
+
++
−−
kkk
N
NNNN
NN
NNNNi
kkk
k



とすると，となる．
全体では，
段，では～
段，では～段，では～が

優先順位キュー（ priority queue ）
 以下の 3 つの操作を提供する抽象データ型
 INSERT(PQ, x)
 優先順位キュー PQ に要素 x を挿入する
 REMOVE(PQ)
 優先順位キュー PQ から最大（最小）の値を持つ要素を取り
除き，それを返す
 PEEK(PQ)
 優先順位キュー PQ の最大（最小）の値を取得する
 応用例：
 ジョブのスケジューリング：
優先度の高いジョブから取り出して実行する
 イベント駆動のシミュレーション：
直近のイベントから順に取り出してシミュレートする

ヒープによる優先順位キューの実
現
def max_heap_insert(PQ, x):
PQ.elems[PQ.heap_size] = x
PQ.heap_size = PQ.heap_size + 1
max_heapify_up(PQ.elems, PQ.heap_size - 1)
def max_heapify_up(A, i):
while i > 0:
j = parent(i)
if A[j] >= A[i]: break
swap(A, i, j)
i = j
 練習問題：
 max_heap_insert(PQ), max_heap_remove(PQ) のコードを書け

解答例
def max_heap_peek(PQ):
return PQ.elems[0]
def max_heap_remove(PQ):
if PQ.heap_size < 1: error(“empty queue”)
max = PQ.elems[0]
PQ.elems[0] = PQ.elems[PQ.heap_size-1]
PQ.heap_size = PQ.heap_size – 1
max_heapify_down(PQ.elems, 0, PQ.heap_size)
return max

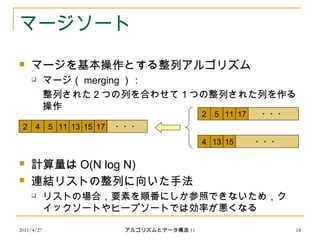
マージソート
 マージを基本操作とする整列アルゴリズム
 マージ（ merging ）：
整列された２つの列を合わせて１つの整列された列を作る
操作
 計算量は O(N log N)
 連結リストの整列に向いた手法
 リストの場合，要素を順番にしか参照できないため，ク
イックソートやヒープソートでは効率が悪くなる
2 115 17
4 1513
2 54 11 13 1715
・・・
・・・
・・・

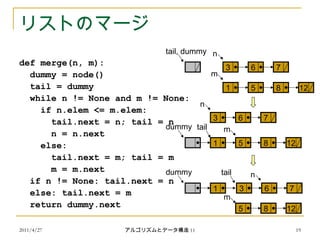
リストのマージ
def merge(n, m):
dummy = node()
tail = dummy
while n != None and m != None:
if n.elem <= m.elem:
tail.next = n; tail = n
n = n.next
else:
tail.next = m; tail = m
m = m.next
if n != None: tail.next = n
else: tail.next = m
return dummy.next
3 6 7
n
1 5 8 12
m
tail, dummy
dummy
1
tail
5 8 12
m
dummy
1
tail
3 6 7
n
5 8 12
m
3 6 7
n

マージソート（リスト版）の実現
 リストを 2 つに分割し，それぞれのリストに対して，再帰的にマー
ジソートを行い，それらを再びマージする．
def merge_sort(n):
if n != None and n.next != None:
p = n; q = n.next
while q != None and q.next != None:
p = p.next; q = q.next.next
m = p.next
p.next = None
return merge(merge_sort(n), merge_sort(m))
else:
return n
リストの中央を見つける巧妙
なテクニック．
p がリストの末尾に到達した
時点で， q は半分ほど進んで
いる

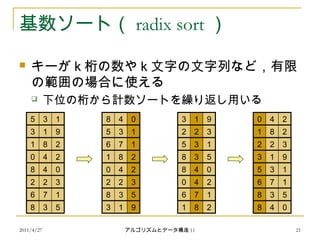
基数ソート（ radix sort ）
 キーが k 桁の数や k 文字の文字列など，有限
の範囲の場合に使える
 下位の桁から計数ソートを繰り返し用いる
3 1 9
1 8 2
0 4 2
8 4 0
2 2 3
6 7 1
8 53
5 13
3 1 9
1 8 2
0 4 2
8 4 0
2 2 3
6 7 1
8 53
5 13
3 1 9
1 8 2
0 4 2
8 4 0
2 2 3
6 7 1
8 53
5 13
3 1 9
1 8 2
0 4 2
8 4 0
2 2 3
6 7 1
8 53
5 13

アルゴリズムとデータ構造11

More Related Content

What's hot

Similar to アルゴリズムとデータ構造11

More from Kenta Hattori

アルゴリズムとデータ構造11