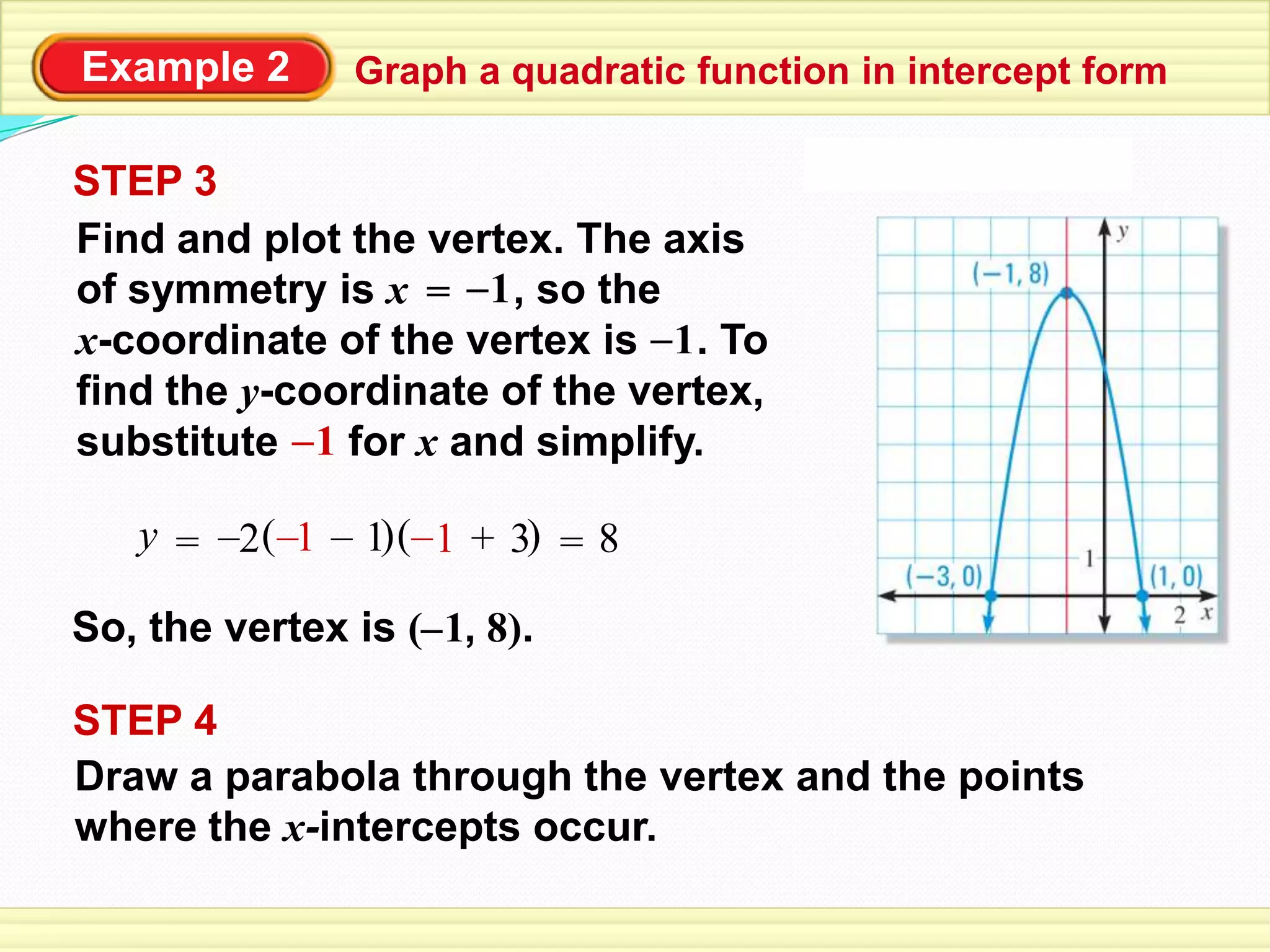
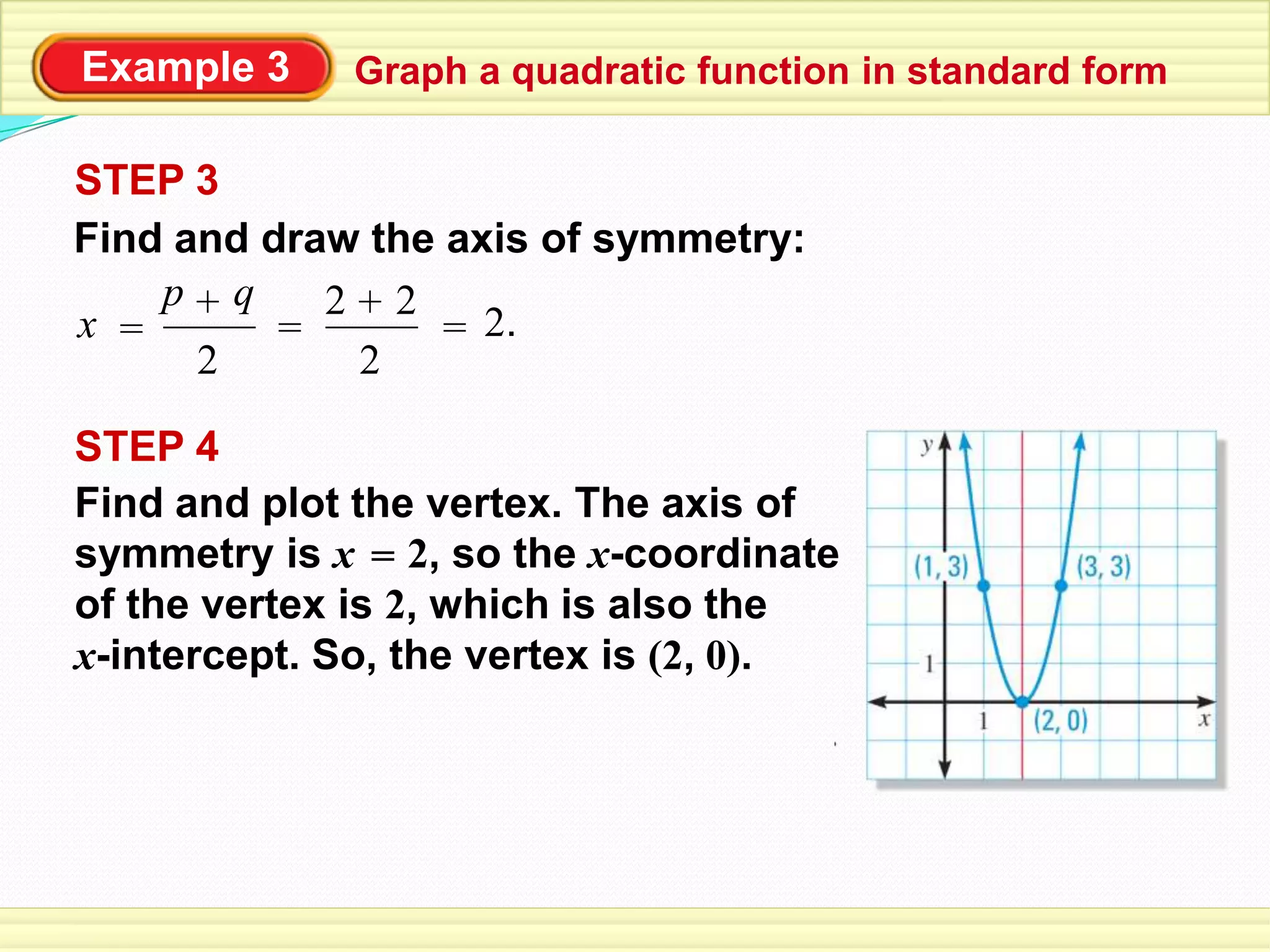
This document provides examples of using quadratic functions in intercept form. It demonstrates how to identify the x-intercepts from the function, graph the function by plotting intercepts and the vertex, write a function given intercepts and a point, and model a real-world scenario like a dolphin's leap using a quadratic function. Key aspects covered include the intercept form equation, finding the vertex and axis of symmetry, and completing the steps to graph or write a quadratic function based on given information.

1. y = a(x - p)(x-q)

2. Characteristics of
 The general form where is
called the intercept form of a quadratic function.
 The x-intercepts are p and q.
 The axis of symmetry is halfway between and
AoS:
 The parabola opens up if and down if
y = a(x- p)(x-q) a ¹ 0
y = a(x - p)(x-q)
(p,0) (q,0)
x =
p+q
2
a > 0 a < 0

3. Example 1 Find x-intercepts
Find the x-intercepts of the graph of ( )1+x= ( ).5x–y –
SOLUTION
To find the x-intercepts, you need to find the values of x
when y = 0.
Write original function.=y ( )1+x ( )5x– –
Substitute 0 for y.=0 ( )1+x ( )5x– –
Zero-product property1+x 5x – = 0= 0 or
Solve for x.x 5x == or1–
The x-intercepts are and 5.1–ANSWER

4. Example 2 Graph a quadratic function in intercept form
Graph ( )1 +x= ( ).3x–y –2
STEP 2
Find and draw the axis of symmetry:
2
q+p
x = =
2
+1 ( )3–
= 1.–
STEP 1
Identify the x-intercepts. The x-intercepts are and
Plot (1, 0) and ( 3, 0).
p = 1
q = –3. –

5. Example 2 Graph a quadratic function in intercept form
STEP 4
Draw a parabola through the vertex and the points
where the x-intercepts occur.
So, the vertex is ( , 8).–1
STEP 3
Find and plot the vertex. The axis
of symmetry is x , so the
x-coordinate of the vertex is . To
find the y-coordinate of the vertex,
substitute for x and simplify.
= –1
–1
–1
( )1 += ( )3–y –2 1– 1– 8=

6. Example 3 Graph a quadratic function in standard form
Graph y = 12 +x2 12.x–3
Rewrite the quadratic function in intercept form.
STEP 1
Write the function.=y 12 +x2 12x–3
Factor out 3.=y 4 +x2 4x–3( )
= x 2–3( )2 Factor the trinomial.
Write in intercept form.= x 2–3( ) x 2–( )
STEP 2
Identify the x-intercepts. There is one x-intercept, 2.
Plot (2, 0).

7. Example 3
STEP 3
Find and draw the axis of symmetry:
2
q+p
x = = = 2.
2
2+2
STEP 4
Find and plot the vertex. The axis of
symmetry is x 2, so the x-coordinate
of the vertex is 2, which is also the
x-intercept. So, the vertex is (2, 0).
=
Graph a quadratic function in standard form

8. Example 3
Draw a parabola through the points.
STEP 6
STEP 5
Plot a point and its reflection. Choose a value for x, say
x 1. When x 1, y 3. Plot (1, 3). By reflecting the
point in the axis of symmetry, you can also plot (3, 3).
= = =
Graph a quadratic function in standard form

9. Example 4 Write a quadratic function in intercept form
Write a quadratic function in intercept form whose
graph has x-intercepts 1 and 3 and passes through
the point (0, 12).
–
–
STEP 1
Substitute the x-intercepts into
The x-intercepts are p
( )px= ( ).y –a qx –
and= 1– q 3.=
( )1x= ( )y +a 3x – Simplify.
–Substitute 1 for p and 3 for q.( x= ( )y –a 3x –( )1– )

10. Example 4 Write a quadratic function in intercept form
Find the value of a in using the given point (0, 12).
STEP 2
( )1x= (y +a 3x – )
–
Simplify.12– = 3a–
Divide each side by 3.–4 = a
ANSWER
y =The function in intercept form is ( )1x (+4 3x – ).
Substitute 0 for x and 12 for y.–( )10= ( )+ 30 –12– a

11. Example 5 Model a parabolic path using intercept form
BIOLOGY
When a dolphin leaps out of
the water, its body follows a parabolic path
through the air.
Write a function whose graph is
the path of the dolphin in the air.
SOLUTION
STEP 1
( )0x= (y a 4x – ),– = (y ax 4x – ).or
Identify the x-intercepts. The dolphin leaves the water at (0, 0) and re-
enters at (4, 0), so the x-intercepts of the path are p 0 and q 4. The
function is of the form
= =

12. Example 5 Model a parabolic path using intercept form
STEP 2
Find the axis of symmetry and the vertex. The axis of symmetry is
The maximum height of 2 meters occurs on the axis of symmetry, so the
vertex of the graph is (2, 2).2
4+0
x = 2.=
Find the value of a. Substitute the coordinates of
the vertex into the function. The vertex is (2, 2), so
2 a (2 – 0)(2 – 4), or a
STEP 3
= =
2
1
– .

13. Example 5 Model a parabolic path using intercept form
ANSWER
The graph of the function
path.
is the dolphin’s
2
1
= – (x 4x – )y

14. 10.3 Warm-Up
Find the x-intercepts of the graph of the quadratic
function.
1.
Graph the quadratic function. Label the vertex, axis of
symmetry, and x-intercept(s).
2.
Write a quadratic function in intercept form whose
graph has the given x-intercept(s) and passes through
the given point.
3. x-intercepts: -6 and 2. point:
y = -2(x -5)(x +1)
y = (x+3)(x-4)
(-2,8)