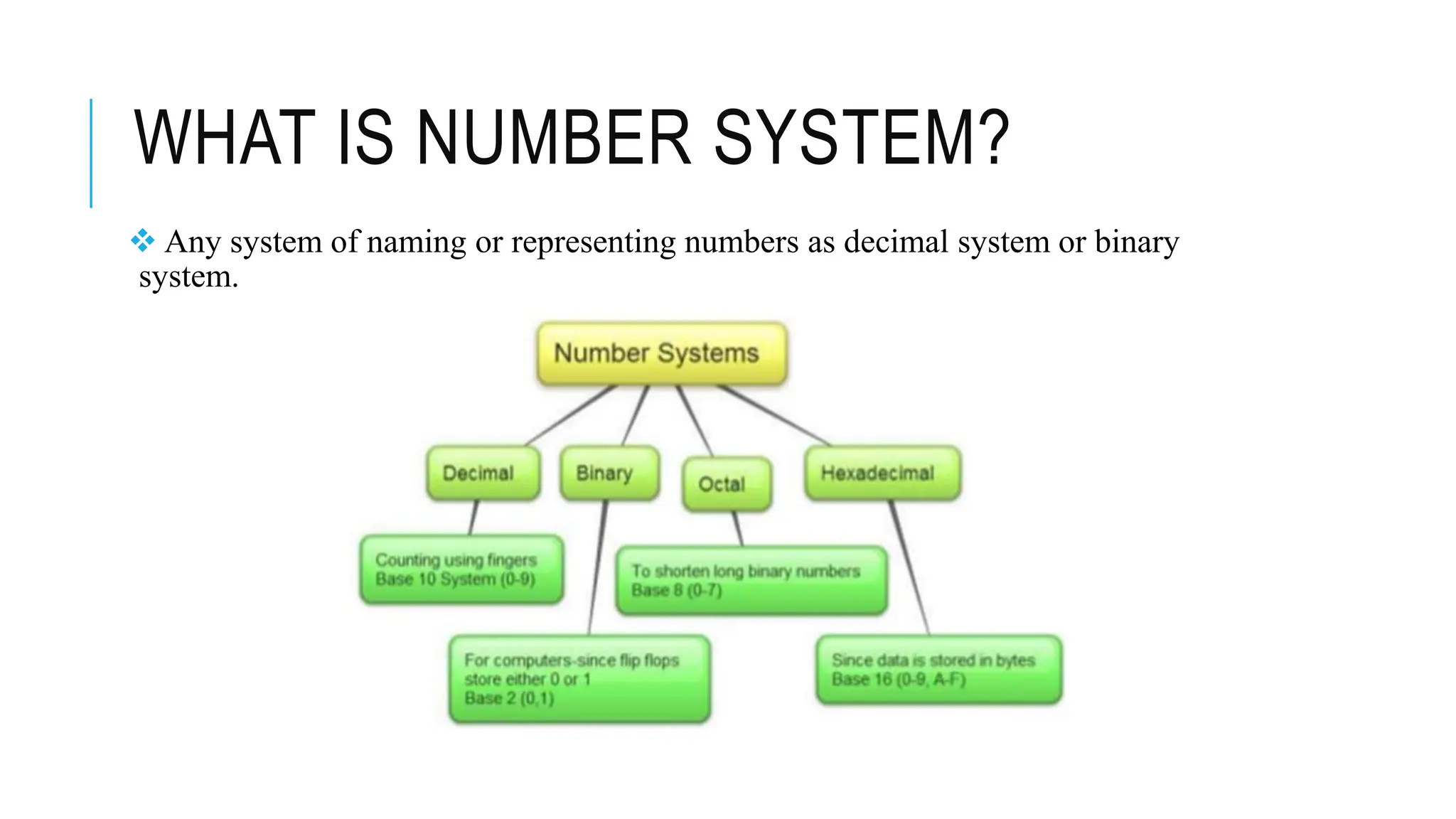
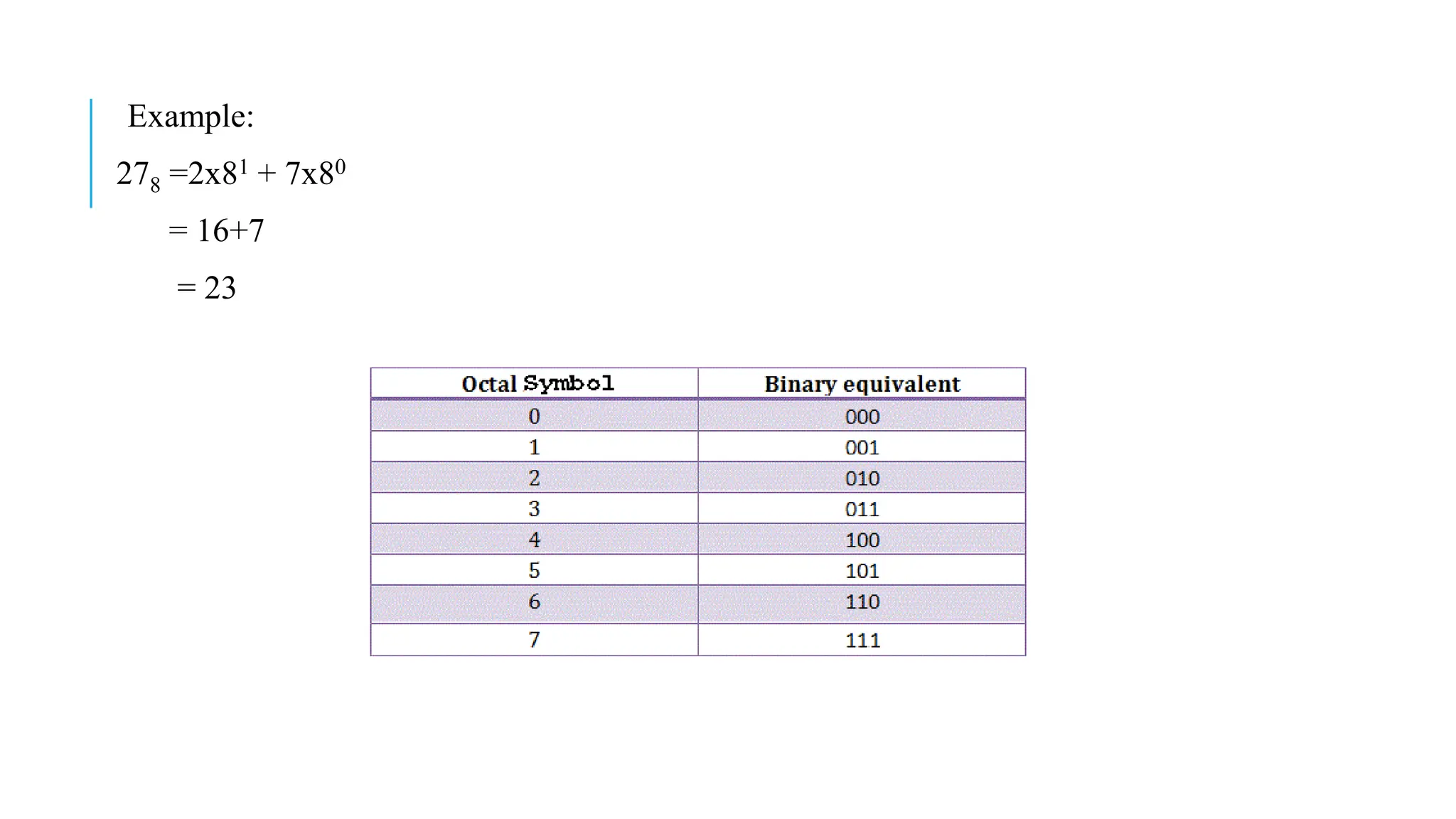
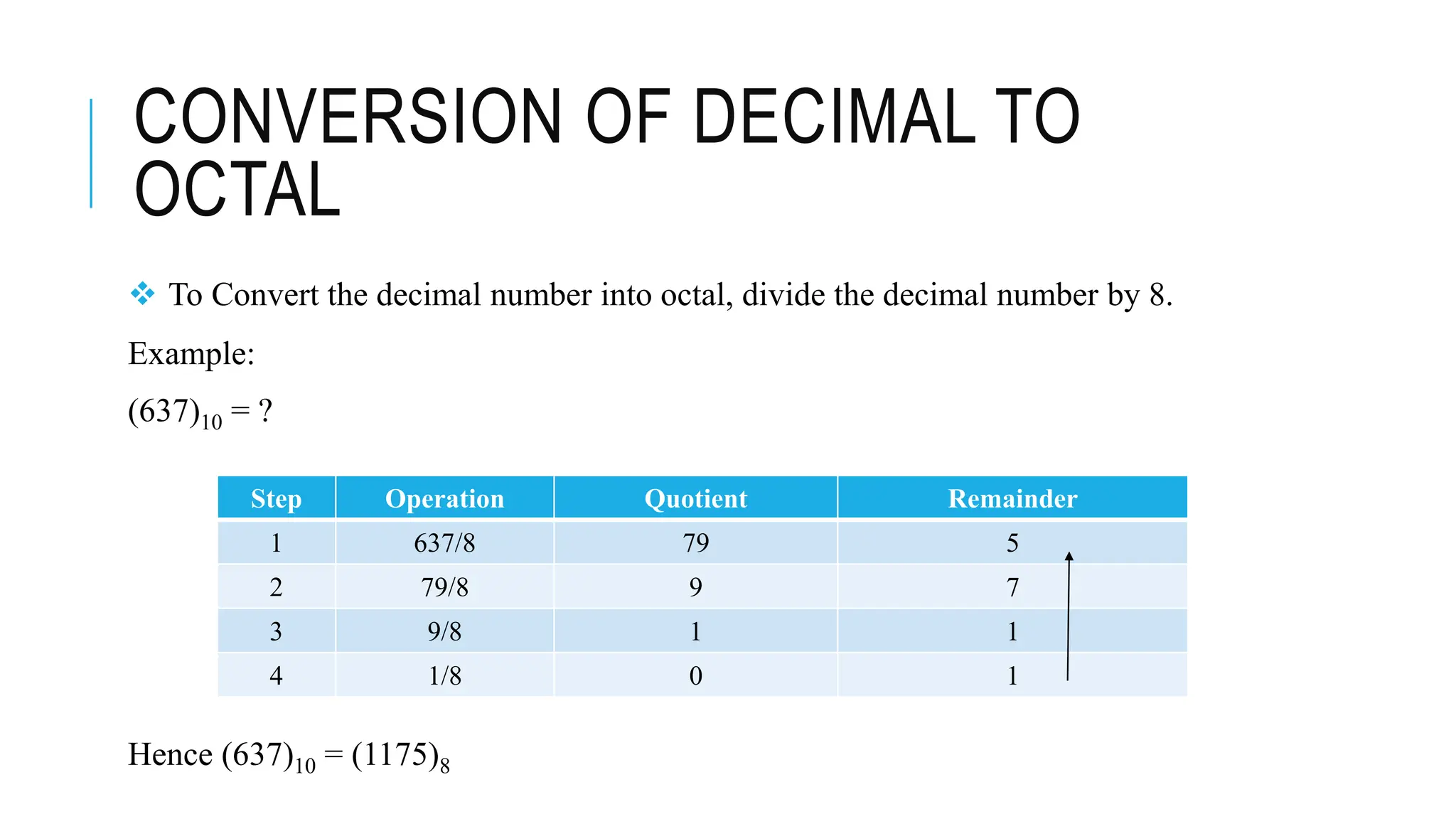
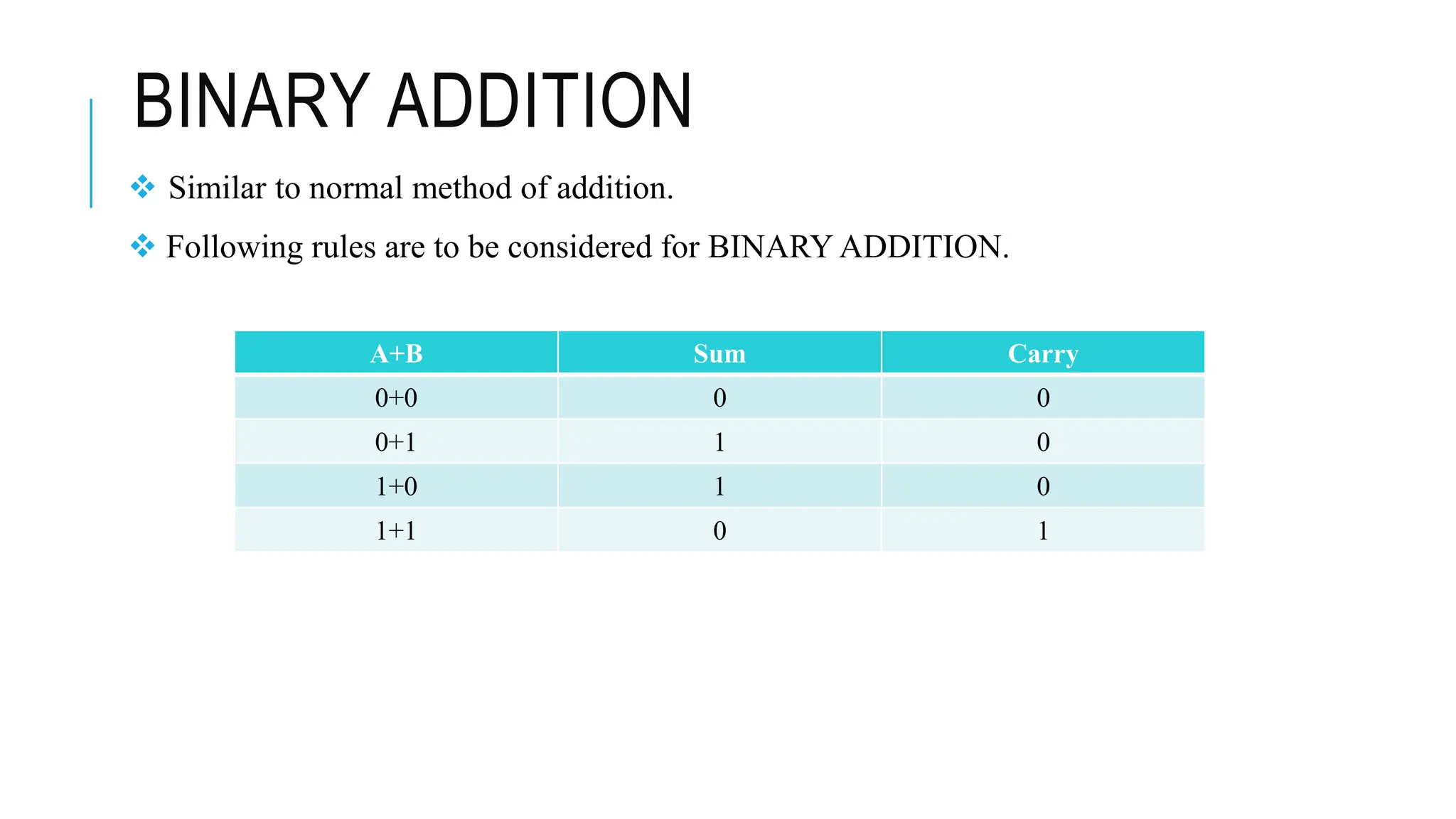
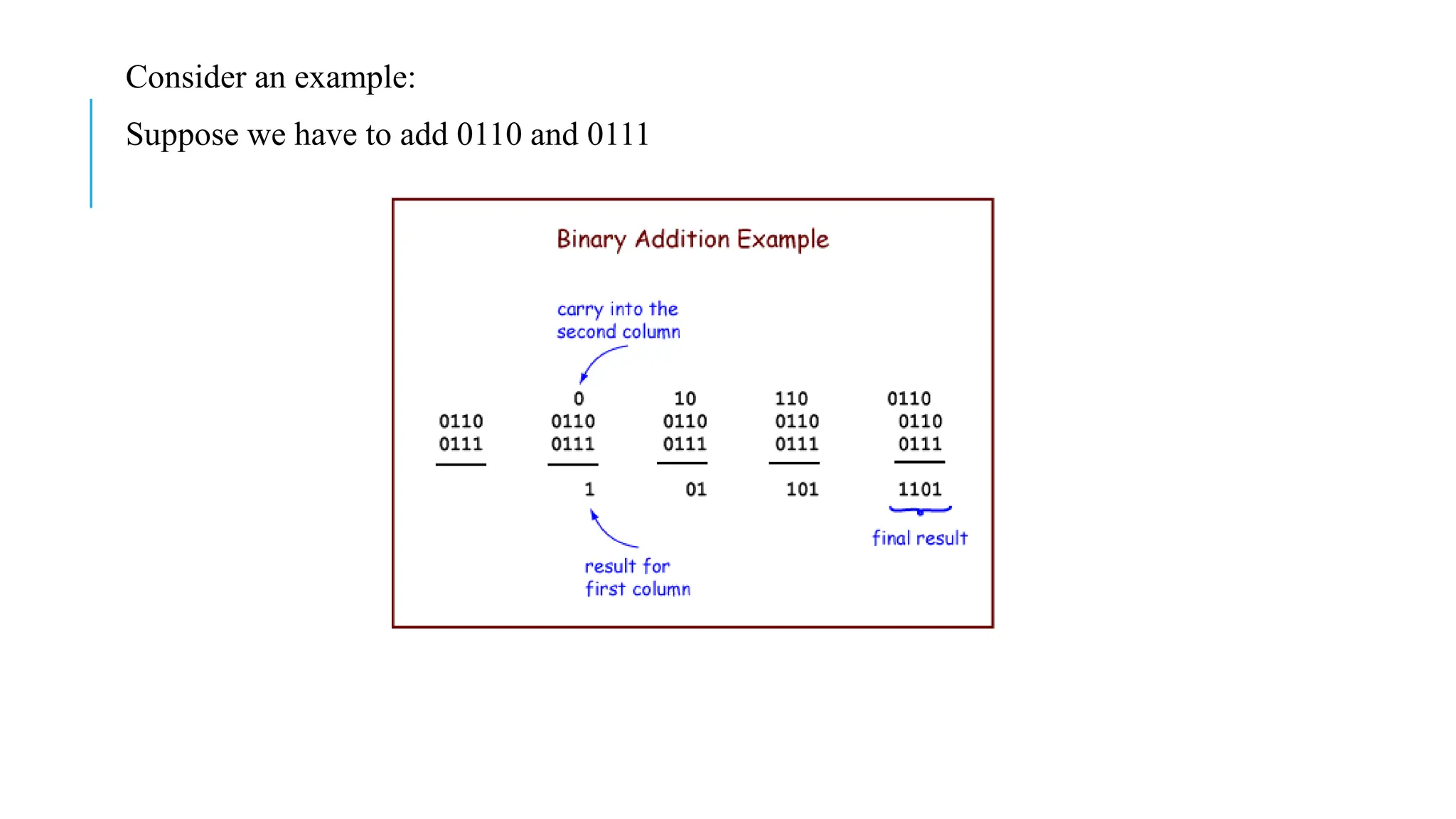
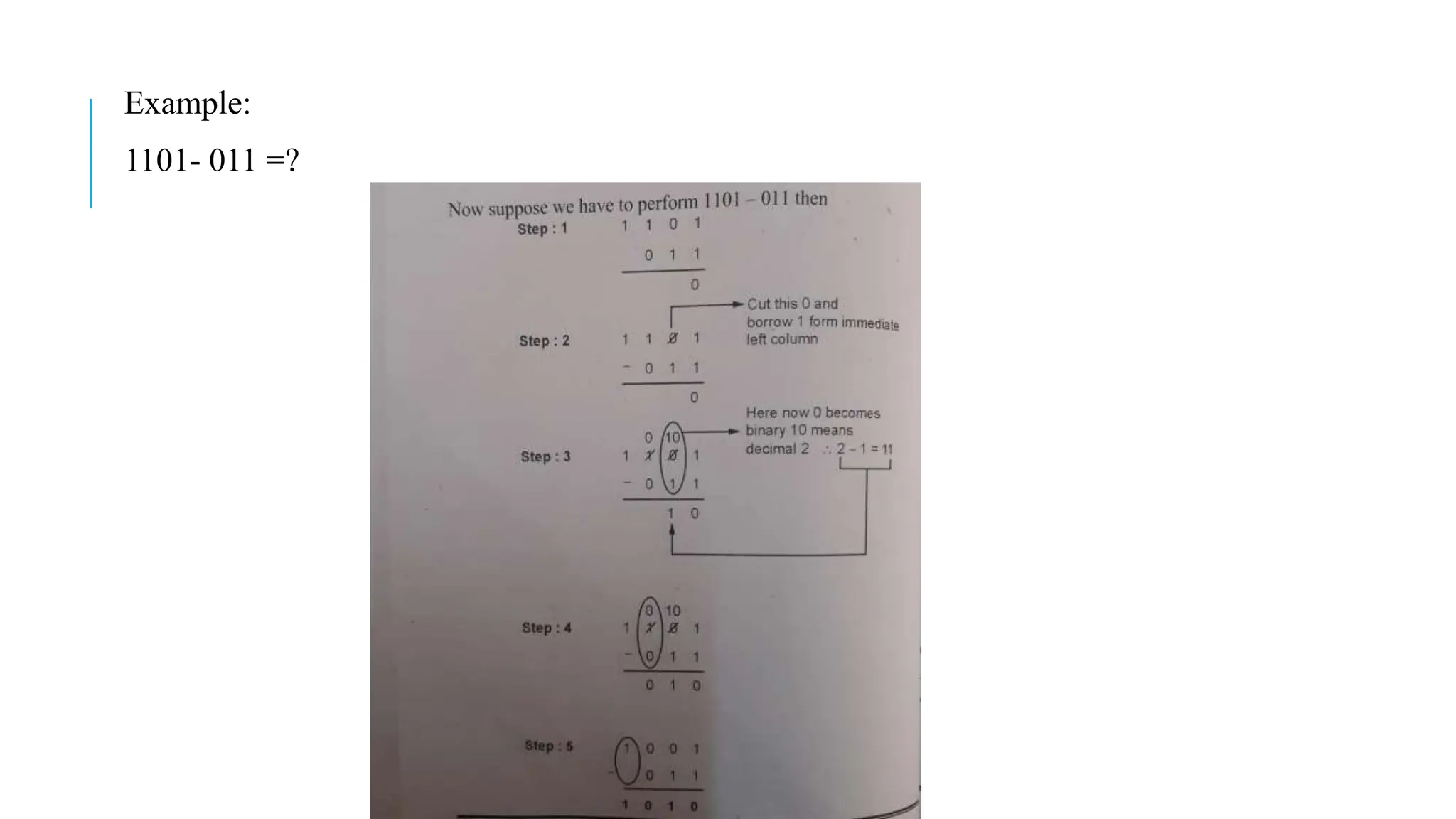
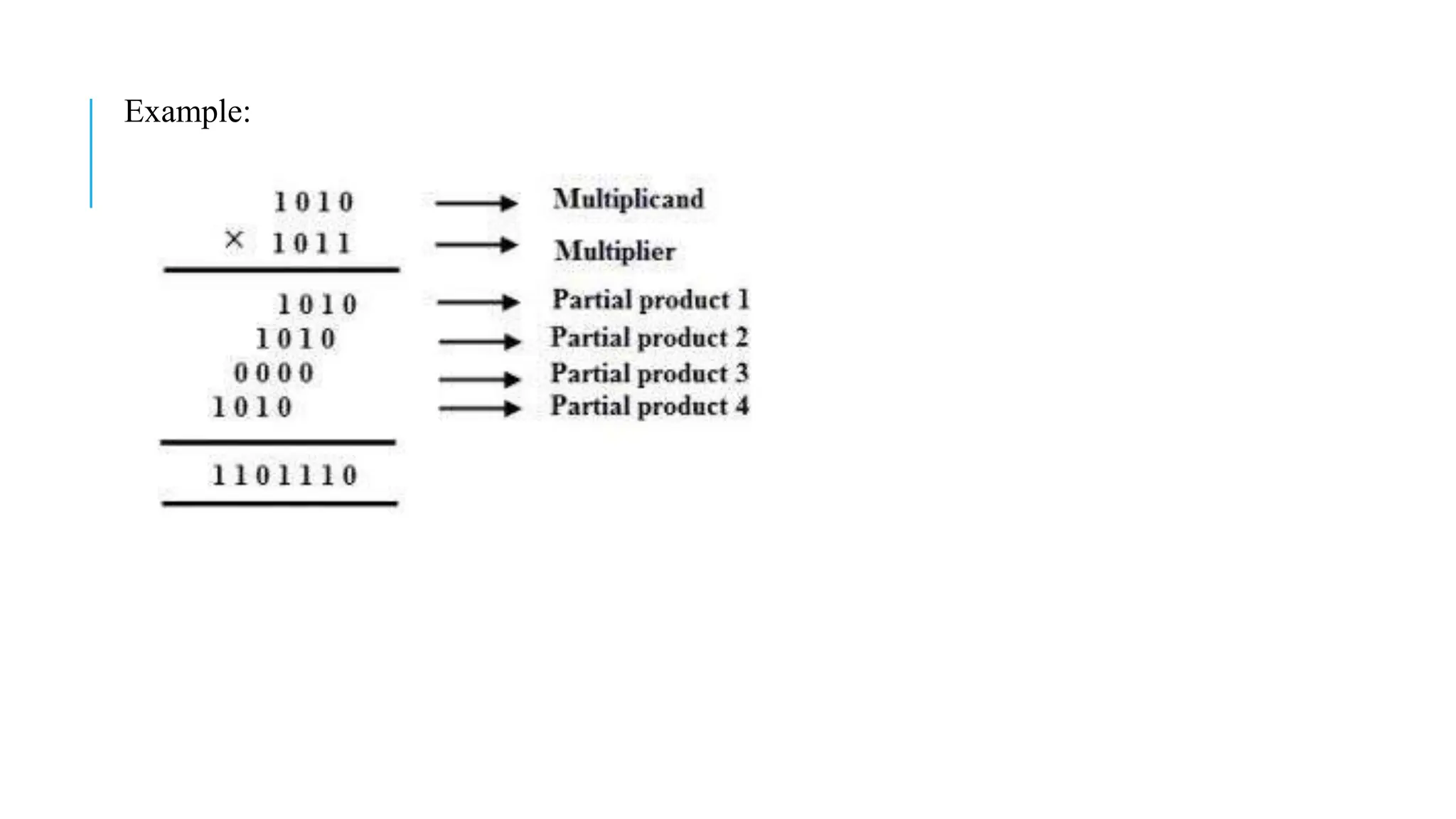
The document explains various number systems, including binary, decimal, octal, and hexadecimal systems, and their applications in computing. It discusses how computers utilize binary representation, arithmetic operations, and conversions between these systems, providing examples for clarity. Additionally, it covers binary addition, subtraction, multiplication, division, and the concepts of one's and two's complements.

1. NUMBER SYSTEM

2. WHAT IS NUMBER SYSTEM?
 Any system of naming or representing numbers as decimal system or binary
system.

3. BINARY NUMBER SYSTEM
 Binary number refers to a term in which a number is expressed using two different
symbols, i.e. 0 and 1.
 This system is used by all modern computers as well as computer based devices.
 Each digit in binary system is known as bit.
binary digits = bits

4. WHY DO COMPUTERS USE BINARY
SYSTEM?
• Processor of each computer is made up of billions of transistors which include a
switch that is activated by electronic signals.
• Digits used in binary system are 0 and 1
0 reflects ON
1 reflects OFF states of a transistor.
• Hence all types of software, music, videos, programs, documents are stored in
binary language.
• Computers only understand base 2, i.e 0 (OFF) and 1 ( ON)
• Every piece of data passed through any part of the computer is done by using base 2
(binary)
• For an n- digit number, the value of a digit depends on its position.

5. Example:
10101 =base is 2
So, it will be calculated as 10101b where b is 2
1x24 + 0x23 + 1x22 + 0x21 + 1x20
16+0+4+0+1 = 21

6. 100011= base is 2
So, it will be calculated as 100011b where b is 2
1x25 + 0x24 + 0x23 0x22 + 1x21 + 1x20
32+0+0+0+2+1 =35
Binary numbers are written as

7. DECIMAL NUMBER SYSTEM
• Decimal number system composes of 10 digits namely 0,1,2,3,4,5,6,7,8 and 9 with base 10.
• It uses a dot (.) i.e. decimal point to denote fractions.
• In this system, position of every digit is important as 1st position shows units place, 2nd of the
left being Tens place and next as Hundreds and so on.

8. Every digit positioned to the left of decimal point is 10 times bigger and every
digit positioned to the right of decimal point is 10 times smaller.

9. Example
In decimal system 253810 is written as
253810 = 2x103 + 5x102 + 3x101 + 8x100
= 2000 + 500 + 30 + 8
= 2538d
All numbers are represented as combination of digits 0-9
Position 3 2 1 0 . -1 -2 -3
Position
value
103 102 101 100 10-1 10-2 10-3
Quantity 1000 100 10 1 1 01 001

10. OCTAL NUMBER SYSTEM
Octal number system requires 8 as a base and 8 digits ( 0,1,2,3,4,5,6 and 7)

11. Example:
278 =2x81 + 7x80
= 16+7
= 23

12. HEXADECIMAL NUMBER SYSTEM
• Hexadecimal number system has 16 as base. It has 10 numeric digits
0,1,2,3,4,5,6,7,8,9 and alphabets from A to F.

13. Example:
BC1216 = 11x163 + 12x162 + 1x161+ 2x160
= 45056 + 3072 +16 + 2
= 48146
BA5916 = 11x163 + 10x162 + 5x161 + 9x160
= 45056 + 2560 + 80 + 9
= 47705

14. CONVERSION OF DECIMAL TO
BINARY
 Divide each decimal number by 2 that will give remainder as 1 or 0.
 The remainder at the top is known as Least Significant Bit (LSB) and at the bottom
is known as Most Significant Bit (MSB).
MSB CAN NEVER BE ZERO!!

15. Example:
Convert 29410 into binary number.
Divide the number by 2
i.e 147 and remainder 0 (LSB)
Again divide by 2
i.e 73 and remainder 1
Divide by 2
i.e 36 and remainder 1
Divide by 2
i.e 18 and remainder 0
Divide by 2
i.e 9 and remainder 0
Divide by 2
i.e 4 and remainder 1
Divide by 2
i.e 2 and remainder 0
Divide by 2
i.e 0 and remainder 1 (MSB)
ANSWER: 101001102

16. CONVERSION OF BINARY TO DECIMAL
 Determine positional value of each digit.
 Multiply the obtained positional value of base 2 by the binary digit.
Example:
Convert (100101)2 to decimal number.
100101= 1x25 + 0x24 + 0x23 + 1x22 + 1x21 + 1x20
= 32+0+0+4+0+1
= 37
Therefore, (100101)2 = (37)10

17. CONVERSION OF OCTAL TO DECIMAL
 Determine the positional value of each digit.
Example:
(62)8 = 6x81 + 2x80
= 48 +2
= 50

18. CONVERSION OF DECIMAL TO
OCTAL
 To Convert the decimal number into octal, divide the decimal number by 8.
Example:
(637)10 = ?
Hence (637)10 = (1175)8
Step Operation Quotient Remainder
1 637/8 79 5
2 79/8 9 7
3 9/8 1 1
4 1/8 0 1

19. CONVERSION OF OCTAL TO
BINARY
 First convert each octal digit into 3 digit binary number
 Combine all the binary groups of 3 digits into single binary number.

20. CONVERSION HEXADECIMAL TO
BINARY
Example 1:
Convert 9AF into binary number.
 Consider binary number for each digit.
Binary number
9 means 1001
A means 1010
F means 1111
9AF= (100110101111)2

21. Example 2:
CE45=?
C = 1100
E = 1110
4 = 0100
5 = 0101
CE45= 1100111001000101

22. CONVERSION OF BINARY TO
HEXADECIMAL
Consider an example,
1110110
 Make groups of four binary digits from right to left.
111 0110
 Add preceding zero.
0111 0110
 Now convert each number from each group to hexadecimal number.
0111 0110
7 6
Hence, (1110110)2 = (76)16

23. BINARY ADDITION
 Similar to normal method of addition.
 Following rules are to be considered for BINARY ADDITION.
A+B Sum Carry
0+0 0 0
0+1 1 0
1+0 1 0
1+1 0 1

24. Example:
1. Add 10010 and 1001
 it will be calculated as
10010
+ 1001
11011
2. Add 00111 and 10101
0111
00111
+10101
11100

25. Consider an example:
Suppose we have to add 0110 and 0111

26. BINARY SUBTRACTION
Binary subtraction is similar to normal subtraction.
BINARY SUBTRACTION TABLE

27. Example:
1101- 011 =?

28. ONE’S COMPLEMENT METHOD
One’s compliment of a binary number is defined as the value obtained by inverting all
the bits.
i.e 0 will be written as 1
1 will be written as 0
Example: 10101 will be written as
01010-------- one’s complement of 10101.
This is useful for obtaining two’s complement of a number.

29. Subtraction using one’s complement.
A) 110101 – 100101
Solution:
Find out 1’s complement of second number.
100101------- 011010
Add 1’s complement to 1st number.
110101
+ 011010
1001111 (Add the carry)
+ 1
010000 -------- ANSWER!
B) 101011 – 111001
111001----- 000110
101011
+000110
110001
No carry, then find out 1’s compliment
of the obtained answer.
110001------ 001110-------- ANSWER!

30. TWO’S COMPLEMENT
This is used to represent negative integer values in binary.
Example:
Find out 2’s complement of 1001101.
Step 1:
Find out 1’s complement of original number.
1001101  0110010
Step 2:
Add 1 to 1’s complemented value
0110010
+ 1
0110011  two’s compliment of 1001101

31. Subtraction using two’s complement.
Example
110110- 010110
Solution:
Find out 2’s complement of second number.
010110  101001 1’s complement
+ 1
101010  2’s complement
Add 2’s complement to 1st number.
110110
+ 101010
1100000
If there’s a carry drop it.
Answer will be 100000
If there’s no carry then find the 2’s complement of the final answer.

32. BINARY MULTIPLICATION
The rules of binary multiplication are as follows.
A X B Multiplication
0 x 0 0
0 x 1 0
1 x 0 0
1 x 1 1

33. Example:

34. BINARY DIVISION
 Division in binary system is same as in decimal system.
 The quotient should be either 1 or 0 depending on the divisor.
A/B
0/1 0
1/1 1

35. Example 1:
10010 / 11
Example 2: