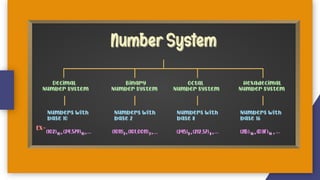
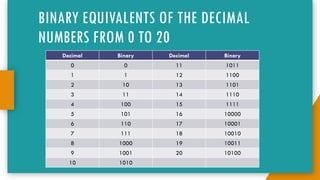
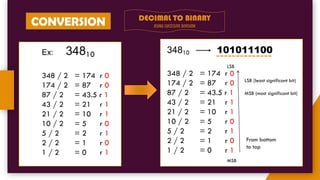
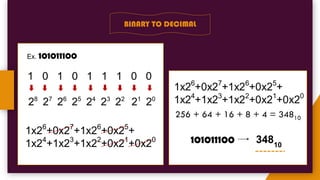
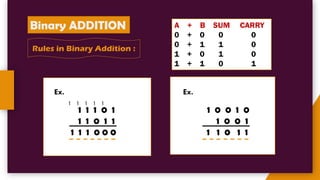
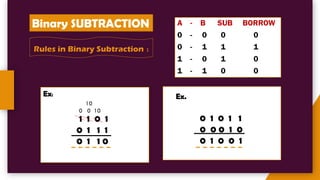
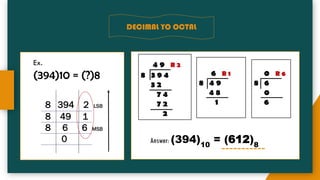
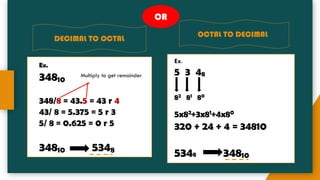
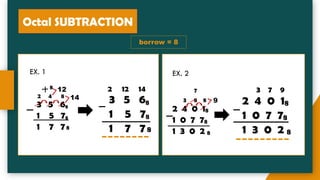
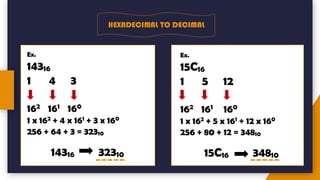
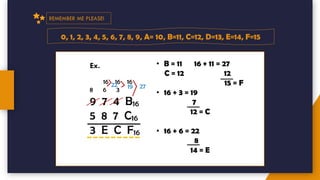
The document provides an introduction to number systems used in computing, detailing various types such as binary, octal, decimal, and hexadecimal systems. It explains how numbers are represented, including conversion methods between different bases and operations like addition and subtraction in these systems. Examples are given to illustrate concepts, particularly focusing on the binary and decimal systems.

1. INTRODUCTION TO
NUMBER SYSTEM

2. What is Number Systems?
Number systems are the technique to
represent numbers in the computer system
architecture, every value that you are saving
or getting into/from computer memory has a
defined number system.

4. Types of Number System
❑ Binary number system
❑ Octal number system
❑ Decimal number system
❑ Hexadecimal (hex) number system

5. DECIMAL NUMBER SYSTEM
The decimal number system was invented and
popularized by the Arabs (and it’s called Arabic number
system).
The decimal number system is said to have base 10
because it uses 10 digits, from 0 to 9.
Digits are positional, which means the digit holds a
different weight(value) depending on the position.
Examples of decimal numbers are:-
(12)10, (345)10, (119)10, (200)10

6. A number system which uses digits from 0 to 9 to represent a number with
base 10 is the decimal system number. The number is expressed in base-10
where each value is denoted by 0 or first nine positive integers. Each
value in this number system has the place value of power 10. It means the
digit at the tens place is ten times greater than the digit at the unit place.
Let us see some more examples:
(92)10 = 9×101+2×100
(200)10 = 2×102+0x101+0x100
The decimal numbers which have digits present on the right side of the
decimal (.) denote each digit with decreasing power of 10. Some examples
are:
(30.2)10= 3×101+0x100+2×10-1
(212.367)10 = 2×102+1×101+2×100+3×10-1+6×10-2+7×10-3

7. BINARY SYSTEM
A Binary number system has only two digits that are 0 and 1. Every
number (value) represents with 0 and 1 in this number system. The base
of binary number system is 2, because it has only two digits.
▪ Bit --- the smallest unit of digital technology, stands for "BInary digiT.“
▪ A byte is a group of eight bits.
▪ A kilobyte is 1,024 bytes or 8,192 bits.
▪ The advantage of the binary system is its simplicity. A computing device
can be created out of anything that has a series of switches, each of
which can alternate between an "on" position and an "off" position.
▪ When a switch is "on" it represents the value of one, and when the
switch is "off" it represents the value of zero

8. BINARY EQUIVALENTS OF THE DECIMAL
NUMBERS FROM 0 TO 20
Decimal Binary Decimal Binary
0 0 11 1011
1 1 12 1100
2 10 13 1101
3 11 14 1110
4 100 15 1111
5 101 16 10000
6 110 17 10001
7 111 18 10010
8 1000 19 10011
9 1001 20 10100
10 1010

9. CONVERSION
Binary to Decimal
In this conversion, a number with base 2 is converted into number with base 10.
Each binary digit here is multiplied by decreasing power of 2. Let us see one
example:
Example:
Convert (11011)2 to decimal number.
1×24+1×23+0x22+1×21+1×20
=16+8+0+2+1
=27
Therefore, (11011)2 = (27)10

10. Convert 1110012 to decimal:
Binary number 1 1 1 0 0 1
Power of 2 25
24 23 22 21 20
1110012 = 1⋅25+1⋅24+1⋅23+0⋅22+0⋅21+1⋅20 = 5710
Convert 101012 to decimal:
Binary number 1 0 1 0 1
Power of 2 24
23 22 21 20
101012 = 1 ⋅ 24 + 0 ⋅ 23 + 1 ⋅ 22 + 0 ⋅ 21 + 1 ⋅ 20 = 2110

11. TRY THIS:
A. 1111112
B. 100102
C. 1110102

12. CONVERSION DECIMAL TO BINARY
USING SUCESSIVE DIVISION
Ex: 34810
348 / 2 = 174 r 0
174 / 2 = 87 r 0
87 / 2 = 43.5 r 1
43 / 2 = 21 r 1
21 / 2 = 10 r 1
10 / 2 = 5 r 0
5 / 2 = 2 r 1
2 / 2 = 1 r 0
1 / 2 = 0 r 1
34810 101011100
LSB
348 / 2 = 174 r 0
174 / 2 = 87 r 0
87 / 2 = 43.5 r 1
43 / 2 = 21 r 1
21 / 2 = 10 r 1
10 / 2 = 5 r 0
5 / 2 = 2 r 1
2 / 2 = 1 r 0
1 / 2 = 0 r 1
MSB
LSB (least significant bit)
MSB (most significant bit)
From bottom
to top

13. Example #2

14. BINARY TO DECIMAL
Ex. 101011100
1 0 1 0 1 1 1 0 0
28
27
26
25
24
23
22
21
20
1x26
+0x27
+1x26
+0x25
+
1x24
+1x23
+1x22
+0x21
+0x20
256 + 64 + 16 + 8 + 4 = 34810
101011100 34810

15. Binary ADDITION
✓Is much like your normal everyday addition (decimal addition),
except that it carries on a value of 2 instead of a value of 10.
For example:
In decimal addition, if you add 8+2 you get ten, which is write as
10; in the sum this gives a digit 0 and a carry of 1.

16. Binary ADDITION A + B SUM CARRY
0 + 0 0 0
0 + 1 1 0
1 + 0 1 0
1 + 1 0 1
Rules in Binary Addition :
Ex.
1 1 1 0 1
1 1 0 1 1
1 1 1 0 0 0
1 1 1 1 1
Ex.
1 0 0 1 0
1 0 0 1
1 1 0 1 1

17. Binary SUBTRACTION
✓Is also similar to that decimal subtraction with the
difference that when 1 is subtracted from 0, it is necessary
to borrow 1 from the next higher order bit and that bit is
reduced by 1 (or is added to the next bit of subtrahend) and
remainder is 1.

18. Binary SUBTRACTION
Ex:
1 1 0 1
0 1 1 1
0 1 1 0
Rules in Binary Subtraction :
A - B SUB BORROW
0 - 0 0 0
0 - 1 1 1
1 - 0 1 0
1 - 1 0 0
10
0 0 10
Ex.
0 1 0 1 1
0 0 0 1 0
0 1 0 0 1

19. OCTAL NUMBER SYSTEM
The octal numeral system, or oct for short, is the base-8
number system, and uses the digits 0 to 7. All the eight
digits from 0 to 8 have same physical meaning as that
of decimal numbers. Octal numerals can be made
from binary numerals by grouping consecutive binary
digits into groups of three (starting from the right).

20. CONVERSION OCTAL TO DECIMAL
Ex.
(370)8
= ( ? )10
3 7 08
82
81
80
= 3 x 8 + 7 x 8 + 0 x 8
= 3 x 64 + 7 x 8 + 0 x 1
= 192 + 56 + 0
= 24810
Answer: (370)8
= (248)10

21. DECIMAL YO OCTAL
Ex.
(394)10 = (?)8
8 394 2 LSB
8 49 1
8 6 6 MSB
0
4 9 R 2
8 3 9 4
3 2
7 4
7 2
2
6 R 1
8 4 9
4 8
1
0 R 6
8 6
0
6
Answer: (394)10
= (612)8

22. DECIMAL TO OCTAL
OCTAL TO DECIMAL
Ex.
34810
348/8 = 43.5 = 43 r 4
43/ 8 = 5.375 = 5 r 3
5/ 8 = 0.625 = 0 r 5
34810 5348
OR
Multiply to get remainder
Ex.
5 3 48
82 81 80
5x82+3x81+4x80
320 + 24 + 4 = 34810
5348 34810

23. OCTAL TO BINARY CONVERSION TABLE

24. Example:
1. Convert octal 1548 to binary:
1548 = 1 5 4 = 1 101 100 = 11011002

25. Octal ADDITION
EX. 1
147
+ 261
4308
Convert to octal :
➢ 7 + 1 = 8
8 8
1 0
➢ 1 + 4 + 6 = 11
8 11
1 3
1 0
carry sum
1 3
carry sum
EX. 2
366.23
+ 243.62
632.058
Convert to octal :
➢ 2 + 6 = 8
8 8
1 0
1 0
carry sum
➢ 1 + 6 + 3 = 10
8 10
1 2
➢ 1 + 6 + 4 = 11
8 11
1 3
1 2
carry sum
1 3
carry sum

26. Octal SUBTRACTION
EX. 1
8
2 4 8
3 5 68
1 5 78
1 7 78
12
14
EX. 2
7
3 8 8
2 4 0 18
1 0 7 78
1 3 0 2 8
2 12 14
3 5 68
1 5 78
1 7 78
borrow = 8
9
3 7 9
2 4 0 18
1 0 7 78
1 3 0 2 8

27. HEXADECIMAL NUMBER SYSTEM
Hexadecimal (or hex) is a base 16 system used
to simplify how binary is represented. A hex
digit can be any of the following 16 digits: 0 1 2
3 4 5 6 7 8 9 A B C D E F.
10 = A 13 = D
11 = B 14 = E
12 = C 15 = F

28. CONVERSION DECIMAL TO HEXADECIMAL
Ex.
28710
287/16 = 17.9375 = 17 r 15
17/16 = 1.0625 = 1 r 1
1/16 = 0.0625 = 0 r 1
1 1 15
F 28710 11F16
Ex.
34810
348/16 = 21.75 = 21 r 12
21/6 = 1.3125 = 1 r 5
1/16 = 0. 0625 = 0 r 1
1 5 12
C 34810 15C16

29. HEXADECIMAL TO DECIMAL
Ex.
15C16
1 5 12
162 161 160
1 x 162 + 5 x 161 + 12 x 160
256 + 80 + 12 = 34810
15C16 34810
Ex.
14316
1 4 3
162 161 160
1 x 162 + 4 x 161 + 3 x 160
256 + 64 + 3 = 32310
14316 32310

30. REMEMBER ME PLEASE!
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A= 10, B=11, C=12, D=13, E=14, F=15
ADDITION
(HEXADECIMAL)
Ex.
5 6 8 9
+ 4 5 7 4
9 B F D
• 9 + 4 = 13 = D
• 8 + 7 = 15 = F
• 6 + 5 = 11 = B

31. REMEMBER ME PLEASE!
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A= 10, B=11, C=12, D=13, E=14, F=15
Ex.
3 F 816
+ 5 B 316
9 A B16
• 8
+3
11 = B
• F = 15
B = 11
26
16 26
1 r 10
1 10 = A
sum carry
not a hexadecimal

32. SUBTRACTION
(HEXADECIMAL)
Ex.
8 16
9 A 516
8 B 416
0 F 116
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A= 10, B=11, C=12, D=13, E=14, F=15
REMEMBER ME PLEASE!
26
• A = 10
B = 11
• 16 + 10 = 26
26
- 11
15 = F

33. 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A= 10, B=11, C=12, D=13, E=14, F=15
REMEMBER ME PLEASE!
Ex.
16 16 16
8 6 3
9 7 4 B16
5 8 7 C16
3 E C F16
27
19
22
• B = 11 16 + 11 = 27
C = 12 12
15 = F
• 16 + 3 = 19
7
12 = C
• 16 + 6 = 22
8
14 = E

34. THANK YOU!