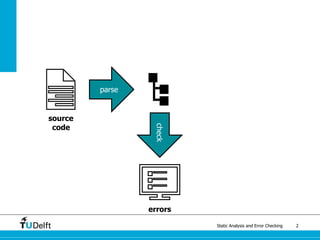
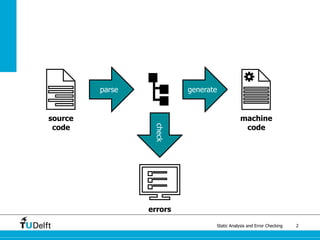
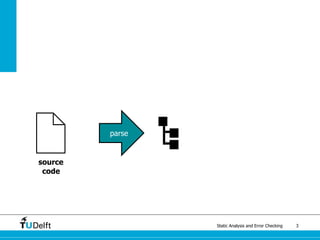
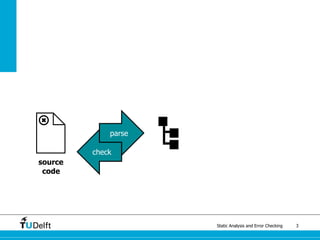
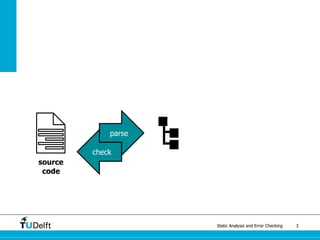
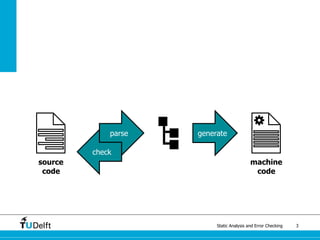
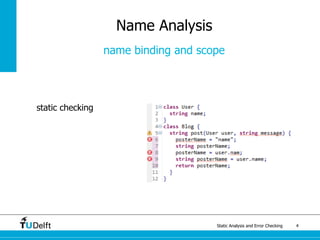
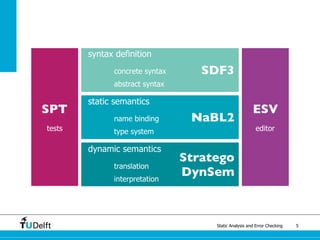
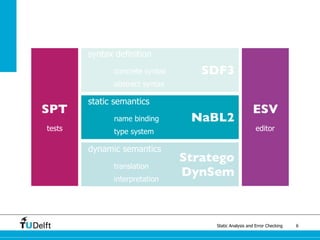
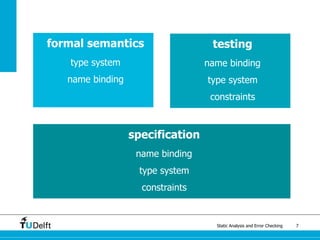
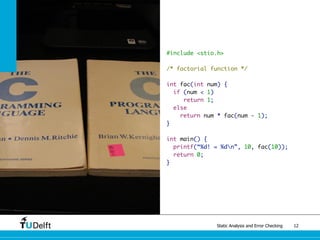
The document discusses static analysis and error checking in compiler construction. It introduces key concepts like parsing source code, performing static semantic checks, and generating machine code. Specific techniques covered include name analysis, type systems, formal semantics, and testing static analysis. Examples are provided using Tiger, a simple imperative language, to illustrate type rules and name binding. The document also discusses theoretical foundations in formal language theory and decidability/complexity.

1. IN4303 2016-2017
Compiler Construction
Introduction to Static Semantics
static analysis and error checking
Guido Wachsmuth, Eelco Visser

2. Static Analysis and Error Checking 2
source
code

3. Static Analysis and Error Checking 2
source
code
parse

4. Static Analysis and Error Checking 2
source
code
errors
parse
check

5. Static Analysis and Error Checking 2
source
code
errors
parse generate
check
machine
code

6. Static Analysis and Error Checking 3
source
code

7. Static Analysis and Error Checking 3
source
code
parse

8. Static Analysis and Error Checking 3
source
code
parse
check

9. Static Analysis and Error Checking 3
source
code
parse
check

10. Static Analysis and Error Checking 3
source
code
parse generate
machine
code
check

11. Static Analysis and Error Checking 4
static checking
Name Analysis
name binding and scope

12. Static Analysis and Error Checking 4
static checking
editor services
Name Analysis
name binding and scope

13. Static Analysis and Error Checking 4
static checking
editor services
transformation
Name Analysis
name binding and scope

14. Static Analysis and Error Checking 4
static checking
editor services
transformation
refactoring
Name Analysis
name binding and scope

15. Static Analysis and Error Checking 4
static checking
editor services
transformation
refactoring
code generation
Name Analysis
name binding and scope

16. Static Analysis and Error Checking
Stratego
DynSem
NaBL2
SDF3
ESV
editor
SPT
tests
5
syntax definition
concrete syntax
abstract syntax
static semantics
name binding
type system
dynamic semantics
translation
interpretation

17. Static Analysis and Error Checking
Stratego
DynSem
NaBL2
SDF3
ESV
editor
SPT
tests
6
syntax definition
concrete syntax
abstract syntax
static semantics
name binding
type system
dynamic semantics
translation
interpretation

18. Static Analysis and Error Checking 7
formal semantics
type system
name binding
testing
name binding
type system
constraints
specification
name binding
type system
constraints

19. Static Analysis and Error Checking 8
Formal Semantics
static semantics

20. Static Analysis and Error Checking 9
word problem χL: Σ*
→ {0,1}
w → 1, if w∈L
w → 0, else
Theoretical Computer Science
decidability & complexity

21. Static Analysis and Error Checking 9
word problem χL: Σ*
→ {0,1}
w → 1, if w∈L
w → 0, else
decidability
type-0: semi-decidable
type-1, type-2, type-3: decidable
Theoretical Computer Science
decidability & complexity

22. Static Analysis and Error Checking 9
word problem χL: Σ*
→ {0,1}
w → 1, if w∈L
w → 0, else
decidability
type-0: semi-decidable
type-1, type-2, type-3: decidable
complexity
type-1: PSPACE-complete
type-2, type-3: P
Theoretical Computer Science
decidability & complexity

23. Static Analysis and Error Checking 9
word problem χL: Σ*
→ {0,1}
w → 1, if w∈L
w → 0, else
decidability
type-0: semi-decidable
type-1, type-2, type-3: decidable
complexity
type-1: PSPACE-complete
type-2, type-3: P
Theoretical Computer Science
decidability & complexity
PSPACE⊇NP⊇P

24. Static Analysis and Error Checking 10
formal grammars
context-sensitive
context-free
regular
theoretical computer science
decidability & complexity

25. Static Analysis and Error Checking 10
formal grammars
context-sensitive
context-free
regular
theoretical computer science
decidability & complexity

26. Static Analysis and Error Checking 10
formal grammars
context-sensitive
context-free
regular
theoretical computer science
decidability & complexity

27. Static Analysis and Error Checking 11
/* factorial function */
let
var x := 0
function fact(n : int) : int =
if n < 1 then 1 else (n * fact(n - 1))
in
for i := 1 to 3 do (
x := x + fact(i);
printint(x);
print(" ")
)
end

28. Static Analysis and Error Checking 12
#include <stio.h>
/* factorial function */
int fac(int num) {
if (num < 1)
return 1;
else
return num * fac(num - 1);
}
int main() {
printf(“%d! = %dn”, 10, fac(10));
return 0;
}

29. Static Analysis and Error Checking 13
class Main {
public static void main(String[] args) {
System.out.println(new Fac().fac(10));
}
}
class Fac {
public int fac(int num) {
int num_aux;
if (num < 1)
num_aux = 1;
else
num_aux = num * this.fac(num - 1);
return num_aux;
}
}

30. Static Analysis and Error Checking 14
static semantics
restricting context-free languages
context-sensitive
language
context-free grammar
L(G) = {w∈Σ*
| S G
*
w}

31. Static Analysis and Error Checking 14
context-free superset
static semantics
restricting context-free languages
context-sensitive
language
context-free grammar
L(G) = {w∈Σ*
| S G
*
w}

32. Static Analysis and Error Checking 14
context-free superset
static semantics
restricting context-free languages
context-sensitive
language
context-free grammar
L(G) = {w∈Σ*
| S G
*
w}

33. Static Analysis and Error Checking 14
context-free superset
static semantics
restricting context-free languages
context-sensitive
language
context-free grammar
L(G) = {w∈Σ*
| S G
*
w}
static semantics
L = {w∈ L(G) | ⊢ w}

34. Static Analysis and Error Checking 14
context-free superset
static semantics
restricting context-free languages
context-sensitive
language
context-free grammar
L(G) = {w∈Σ*
| S G
*
w}
static semantics
L = {w∈ L(G) | ⊢ w}
judgements
well-formed ⊢ w
well-typed E ⊢ e : t

35. Static Analysis and Error Checking 15
Formal Semantics
type systems

36. Static Analysis and Error Checking 16
Tiger
type system
E ⊢ i : int
E ⊢ s : string
E ⊢ nil : ⊥

37. Static Analysis and Error Checking 17
Tiger
type system
E ⊢ () : ∅
E ⊢ e1 : t1
E ⊢ e2 : t2
E ⊢ e1 ; e2 : t2

38. Static Analysis and Error Checking 18
Tiger
type system
E ⊢ e1 : int
E ⊢ e2 : int
E ⊢ e1 + e2 : int
E ⊢ e1 : int
E ⊢ e2 : int
E ⊢ e1 < e2 : int
E ⊢ e1 : string
E ⊢ e2 : string
E ⊢ e1 < e2 : int
E ⊢ e1 : array of t
E ⊢ e2 : int
E ⊢ e1[e2] : t

39. Static Analysis and Error Checking 19
Tiger
type system
E ⊢ e1 : t1
E ⊢ e2 : t2
t1 ≅ t2
E ⊢ e1 = e2 : int
t1 <: t2
t1 ≅ t2
t2 <: t1
t1 ≅ t2
t ≠ ∅
t ≅ t
⊥<: {f1, …, fn}
⊥<: array of t

40. Static Analysis and Error Checking 20
Tiger
type system
E ⊢ e1 : t1
E ⊢ e2 : t2
t1 ≅ t2
E ⊢ e1 := e2 : ∅
E ⊢ e1 : int
E ⊢ e2 : t1
E ⊢ e3 : t2
t1 ≅ t2
E ⊢ if e1 then e2 else e3: t2

41. Static Analysis and Error Checking 21
Formal Semantics
name binding

42. Static Analysis and Error Checking 22
Tiger
scoping
let
type t = u
type u = int
var x: u := 0
in
x := 42 ;
let
type u = t
var y: u := 0
in
y := 42
end
end

43. Static Analysis and Error Checking 22
Tiger
scoping
let
type t = u
type u = int
var x: u := 0
in
x := 42 ;
let
type u = t
var y: u := 0
in
y := 42
end
end

44. Static Analysis and Error Checking 22
Tiger
scoping
let
type t = u
type u = int
var x: u := 0
in
x := 42 ;
let
type u = t
var y: u := 0
in
y := 42
end
end

45. Static Analysis and Error Checking 22
Tiger
scoping
let
type t = u
type u = int
var x: u := 0
in
x := 42 ;
let
type u = t
var y: u := 0
in
y := 42
end
end

46. Static Analysis and Error Checking 22
Tiger
scoping
let
type t = u
type u = int
var x: u := 0
in
x := 42 ;
let
type u = t
var y: u := 0
in
y := 42
end
end

47. Static Analysis and Error Checking 23
Tiger
variable names
E ⊢ e1 : t1
t ≅ t1
E ⊕ v ↦ t ⊢ e2 : t2
E ⊢ let var v : t = e1 in e2: t2
E(v) = t
E ⊢ v : t

48. Static Analysis and Error Checking 24
Tiger
function names
E ⊕ v1 ↦ t1 ,…, vn ↦ tn ⊢ e1 : tf
E ⊕ f ↦ t1 × … × tn → tf ⊢ e2 : t
E ⊢ let
function f (v1 : t1, …, vn : tn) = e1
in e2: t
E(f) = t1 × … × tn → tf
e1 : t1
…
en : tn
E ⊢ f (e1, …, en) : t

49. Static Analysis and Error Checking 25
Testing Static Analysis

50. Static Analysis and Error Checking 26
test outer name [[
let type t = u
type [[u]] = int
var x: [[u]] := 0
in
x := 42 ;
let type u = t
var y: u := 0
in
y := 42
end
end
]] resolve #2 to #1
test inner name [[
let type t = u
type u = int
var x: u := 0
in
x := 42 ;
let type [[u]] = t
var y: [[u]] := 0
in
y := 42
end
end
]] resolve #2 to #1
Testing
name binding

51. Static Analysis and Error Checking 27
test integer constant [[
let type t = u
type u = int
var x: u := 0
in
x := 42 ;
let type u = t
var y: u := 0
in
y := [[42]]
end
end
]] run get-type to IntTy()
test variable reference [[
let type t = u
type u = int
var x: u := 0
in
x := 42 ;
let type u = t
var y: u := 0
in
y := [[x]]
end
end
]] run get-type to IntTy()
Testing
type system

52. Static Analysis and Error Checking 28
test undefined variable [[
let type t = u
type u = int
var x: u := 0
in
x := 42 ;
let type u = t
var y: u := 0
in
y := [[z]]
end
end
]] 1 error
test type error [[
let type t = u
type u = string
var x: u := 0
in
x := 42 ;
let type u = t
var y: u := 0
in
y := [[x]]
end
end
]] 1 error
Testing
constraints

53. Static Analysis and Error Checking 29
context-free superset
Testing
static semantics
language

54. Static Analysis and Error Checking 30
Next

55. Imperative and Object-Oriented Languages
Next
Week 5
• lexical analysis: from regular grammar to DFA
31

56. Imperative and Object-Oriented Languages
Next
Week 5
• lexical analysis: from regular grammar to DFA
Week 6
• name binding rules
• name resolution with scope graphs
31

57. Imperative and Object-Oriented Languages
Next
Week 5
• lexical analysis: from regular grammar to DFA
Week 6
• name binding rules
• name resolution with scope graphs
Week 8
• constraint-based type analysis
31

58. Imperative and Object-Oriented Languages
Next
Week 5
• lexical analysis: from regular grammar to DFA
Week 6
• name binding rules
• name resolution with scope graphs
Week 8
• constraint-based type analysis
Q2
• dynamic semantics, code generation, optimization
• parsing algorithms
31

59. Static Analysis and Error Checking 32
Spoofax
annotated terms
t{t1, ..., tn}
add additional information to a term but preserve its signature

60. Static Analysis and Error Checking 33
Except where otherwise noted, this work is licensed under

61. Static Analysis and Error Checking 34
attribution
slide title author license
1 Inspection Kent Wien CC BY-NC 2.0
2, 3 PICOL icons Melih Bilgil CC BY 3.0
10 Noam Chomsky Maria Castelló Solbes CC BY-NC-SA 2.0
11, 16-20, 22-24 Tiger Bernard Landgraf CC BY-SA 3.0
12 The C Programming Language Bill Bradford CC BY 2.0
13 Italian Java book cover