Guido Wachsmuth, profile picture
Uploaded byGuido Wachsmuth
PDF, PPTX1,950 views

Declarative Semantics Definition - Term Rewriting

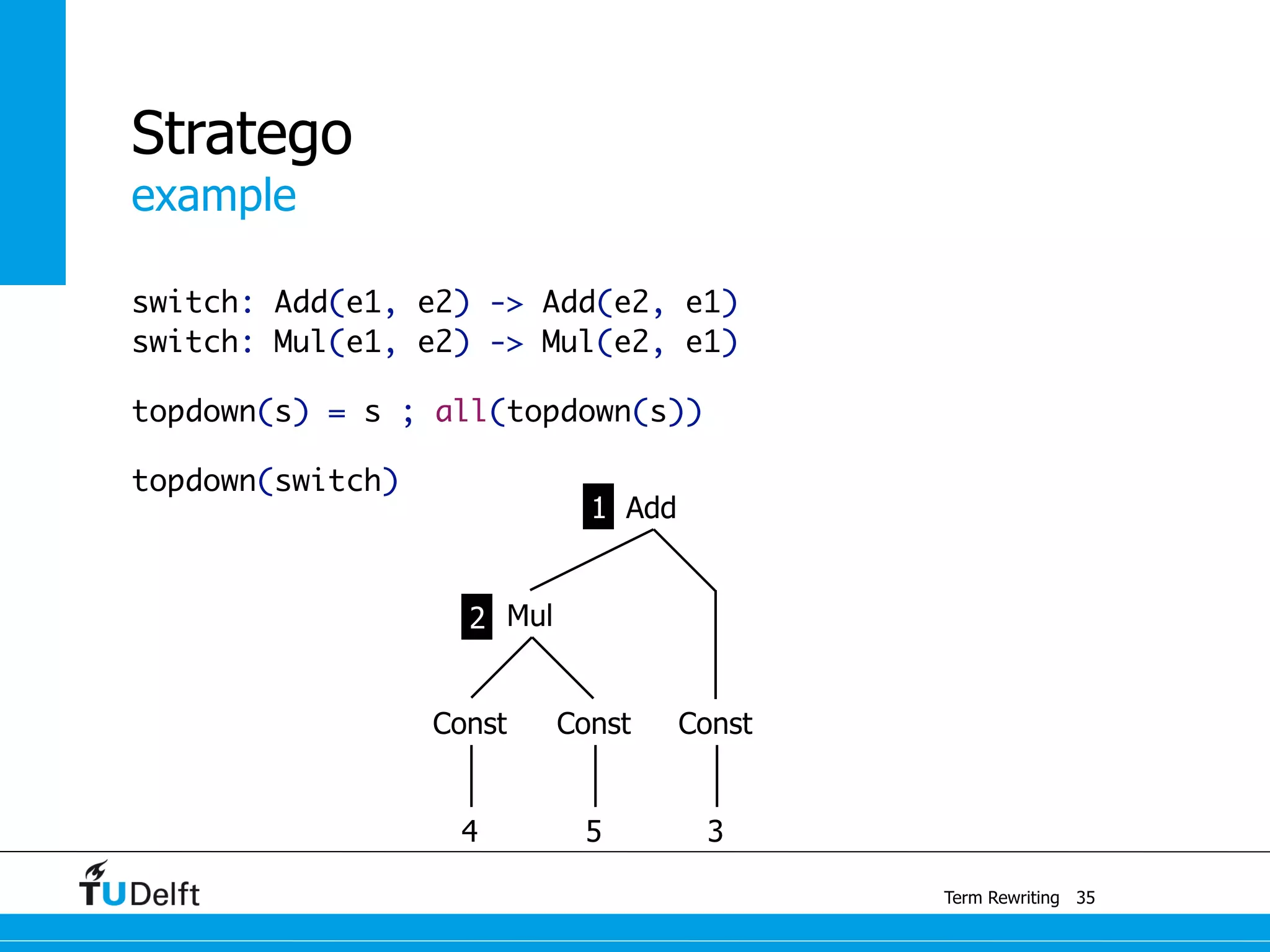
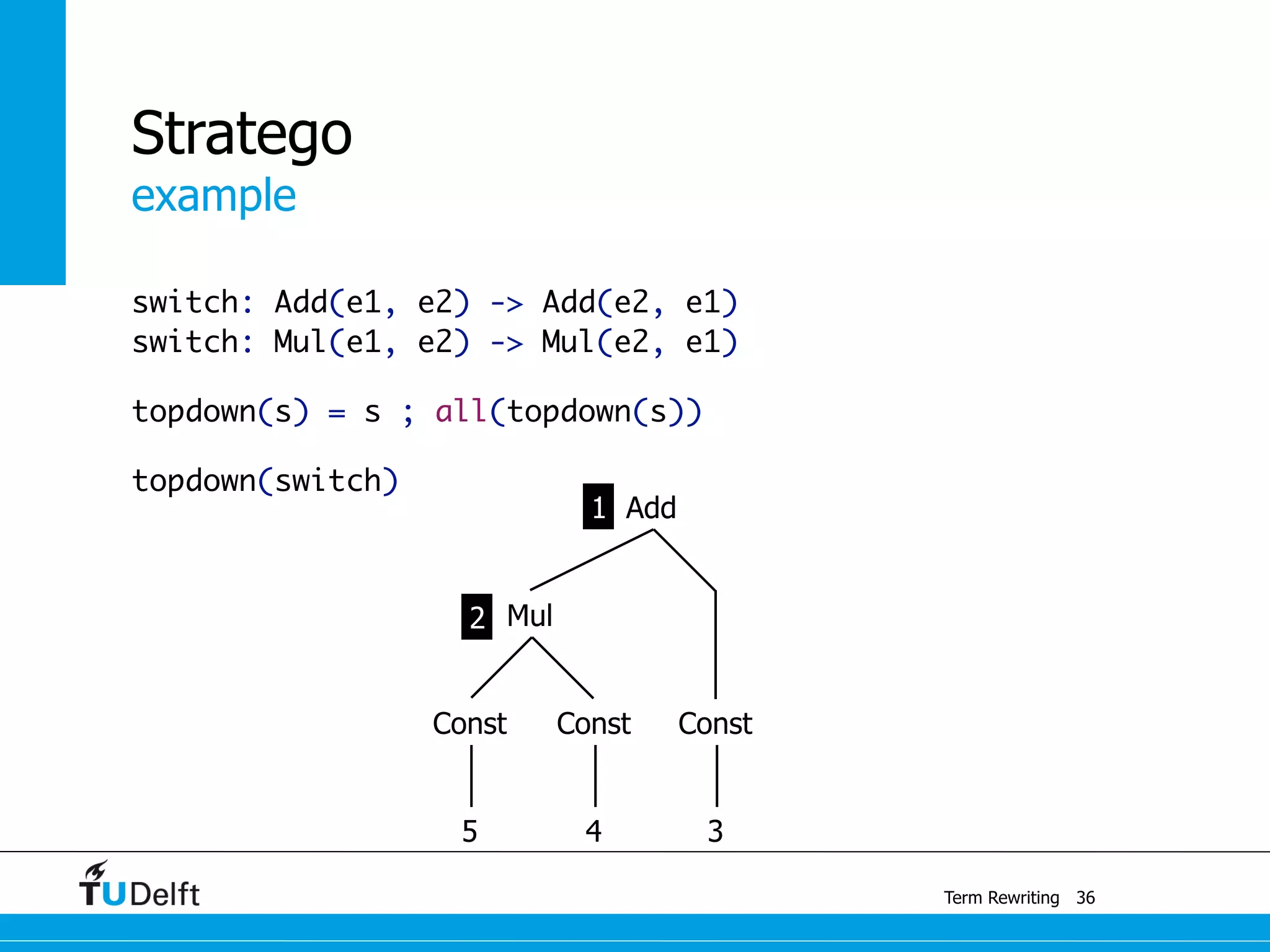
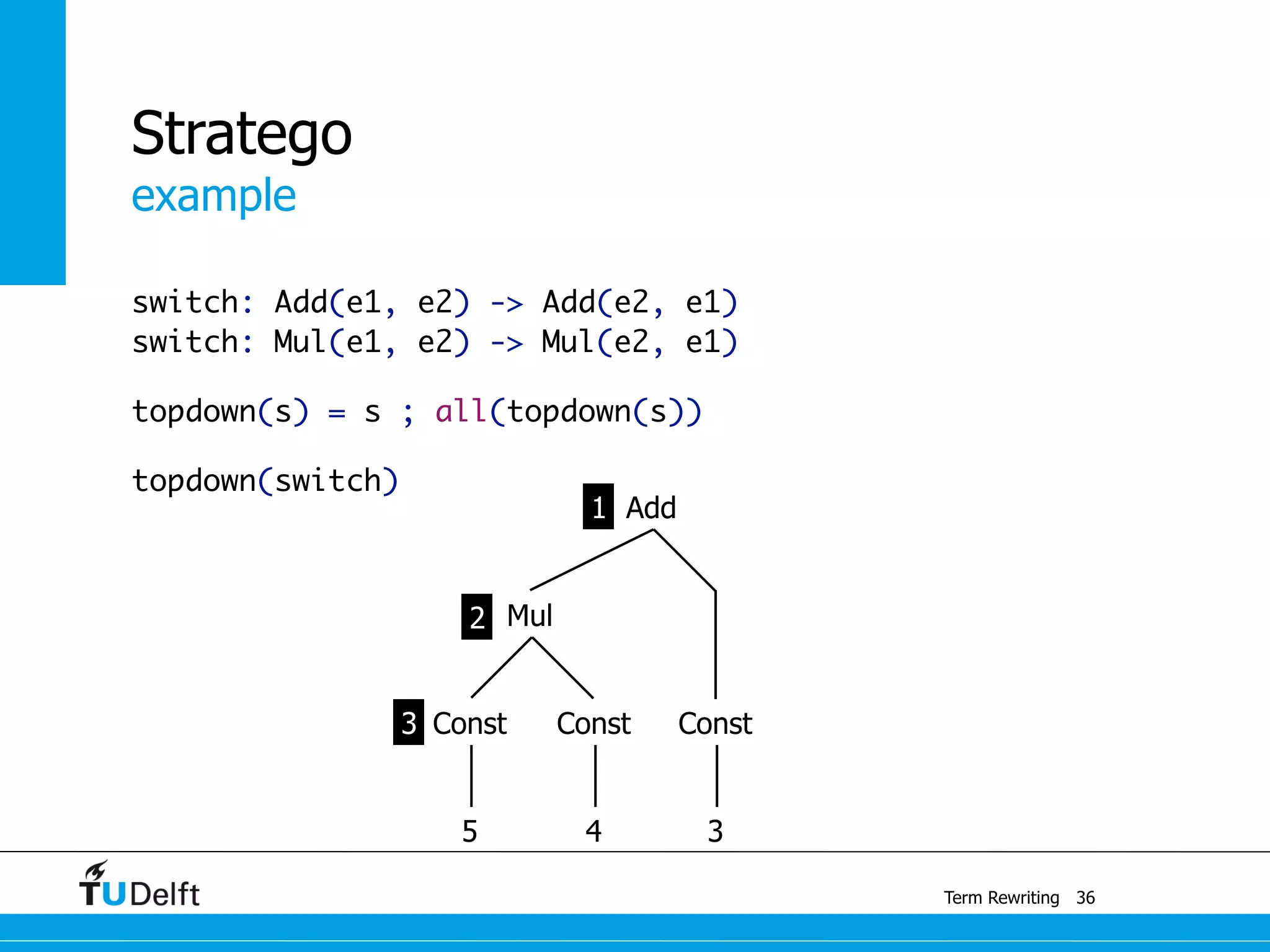
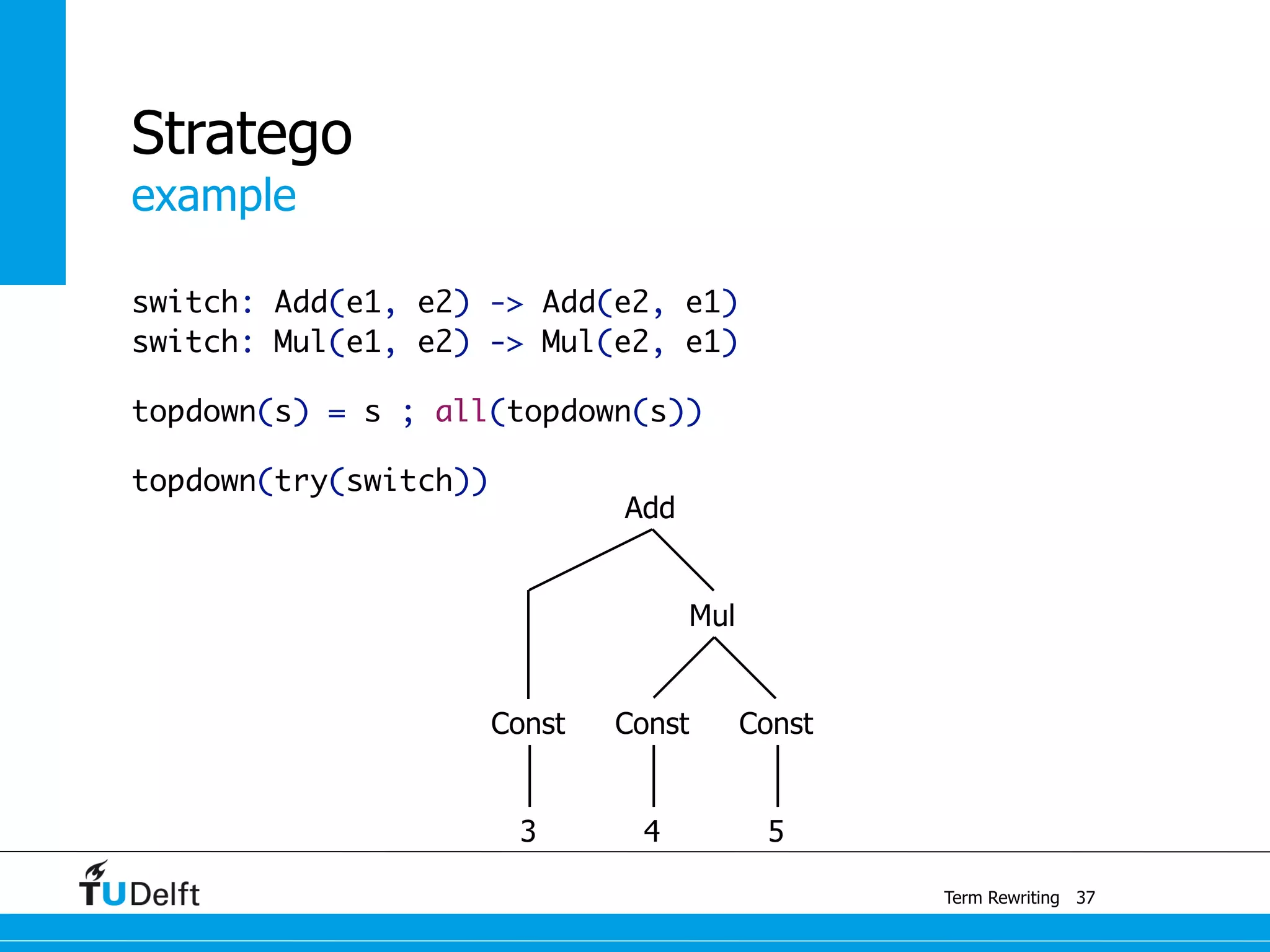
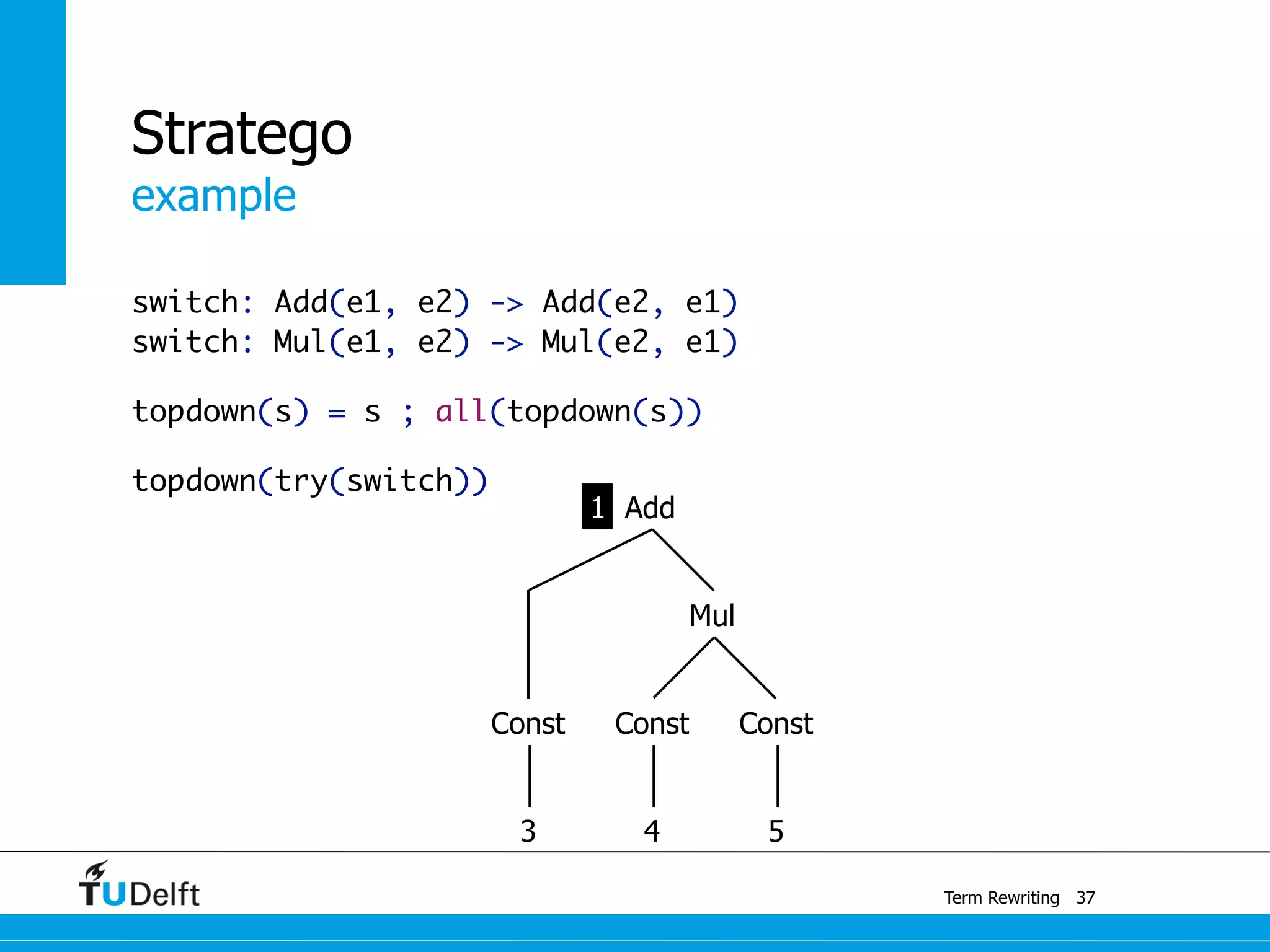
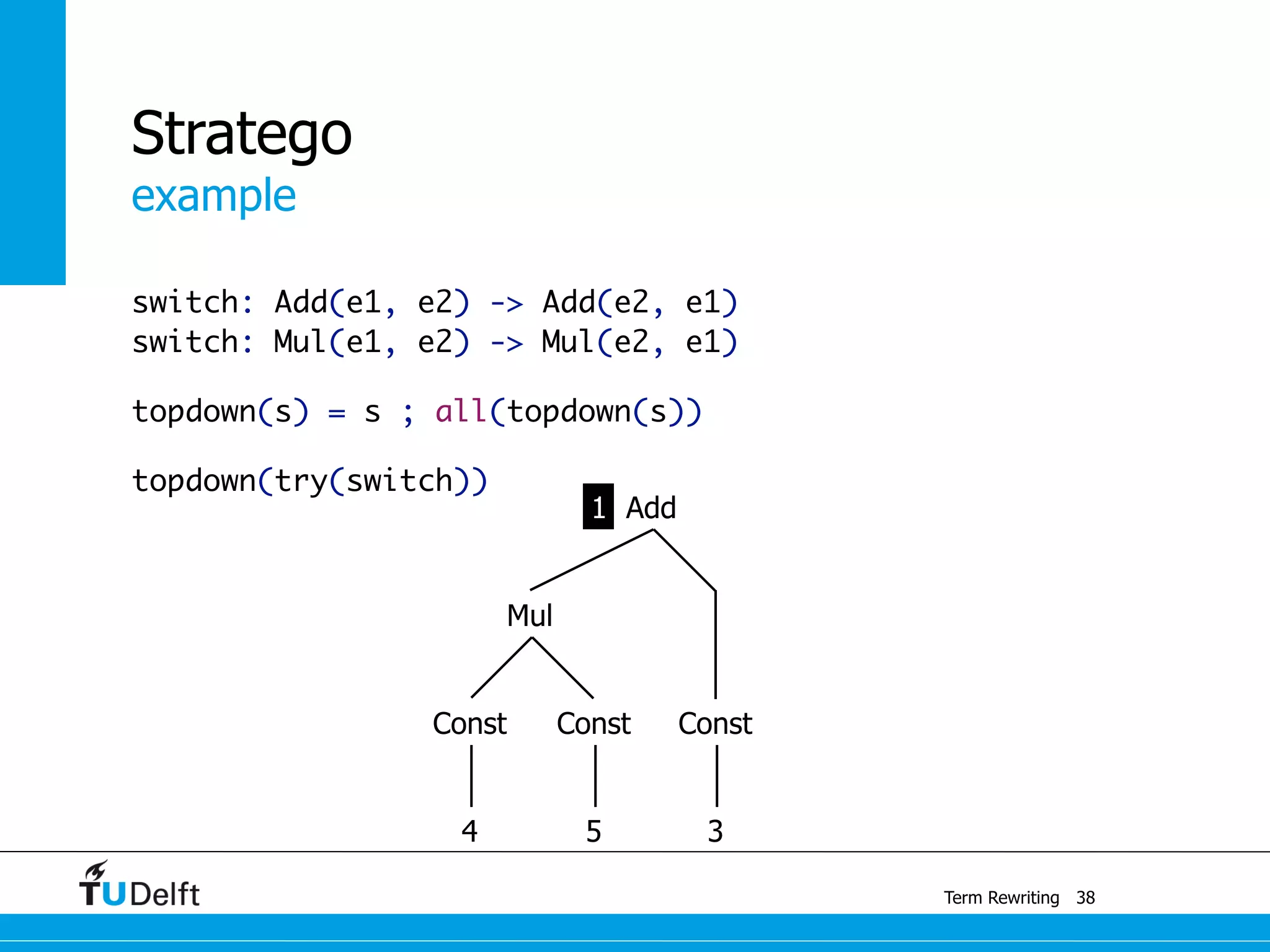
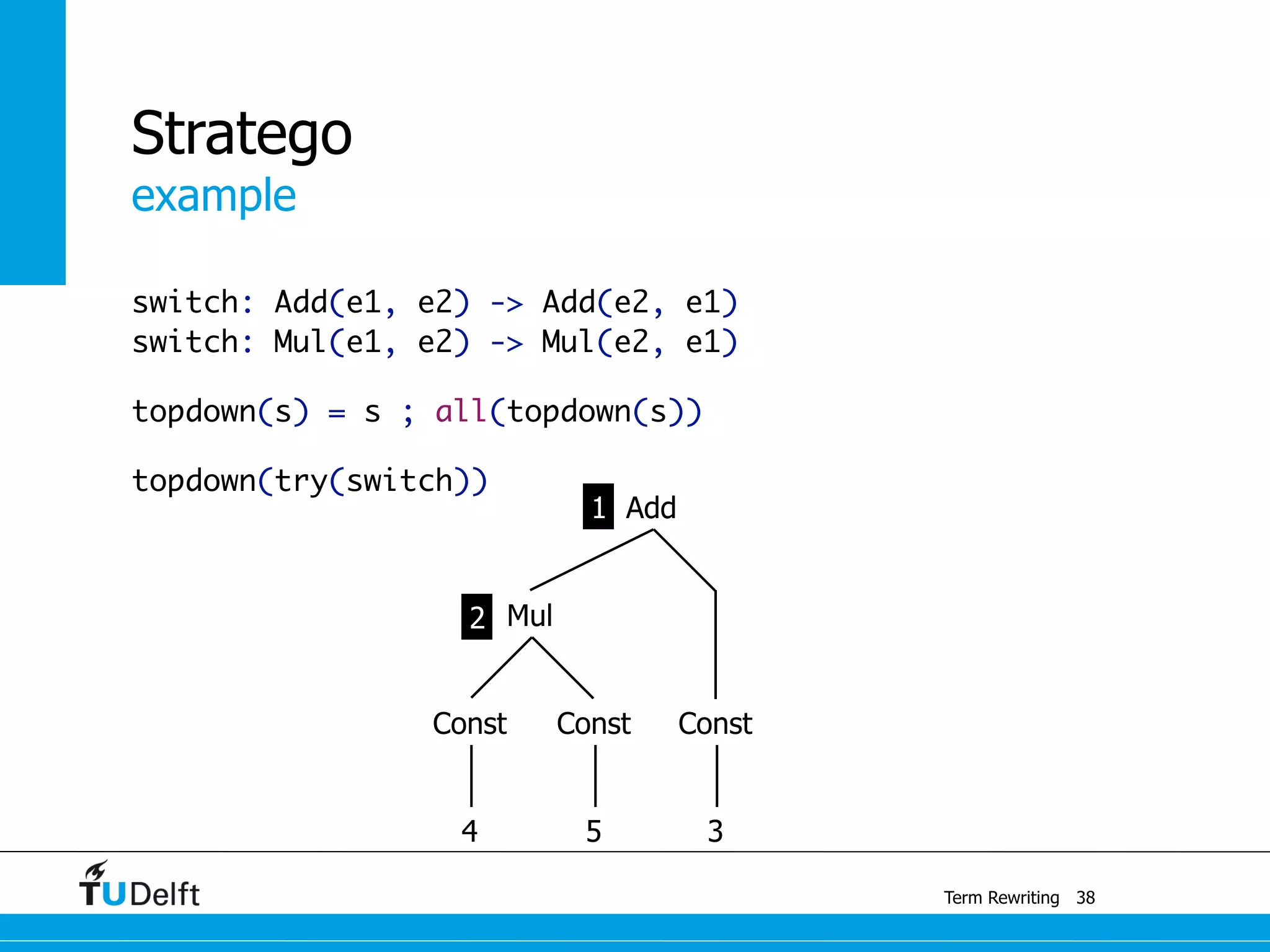
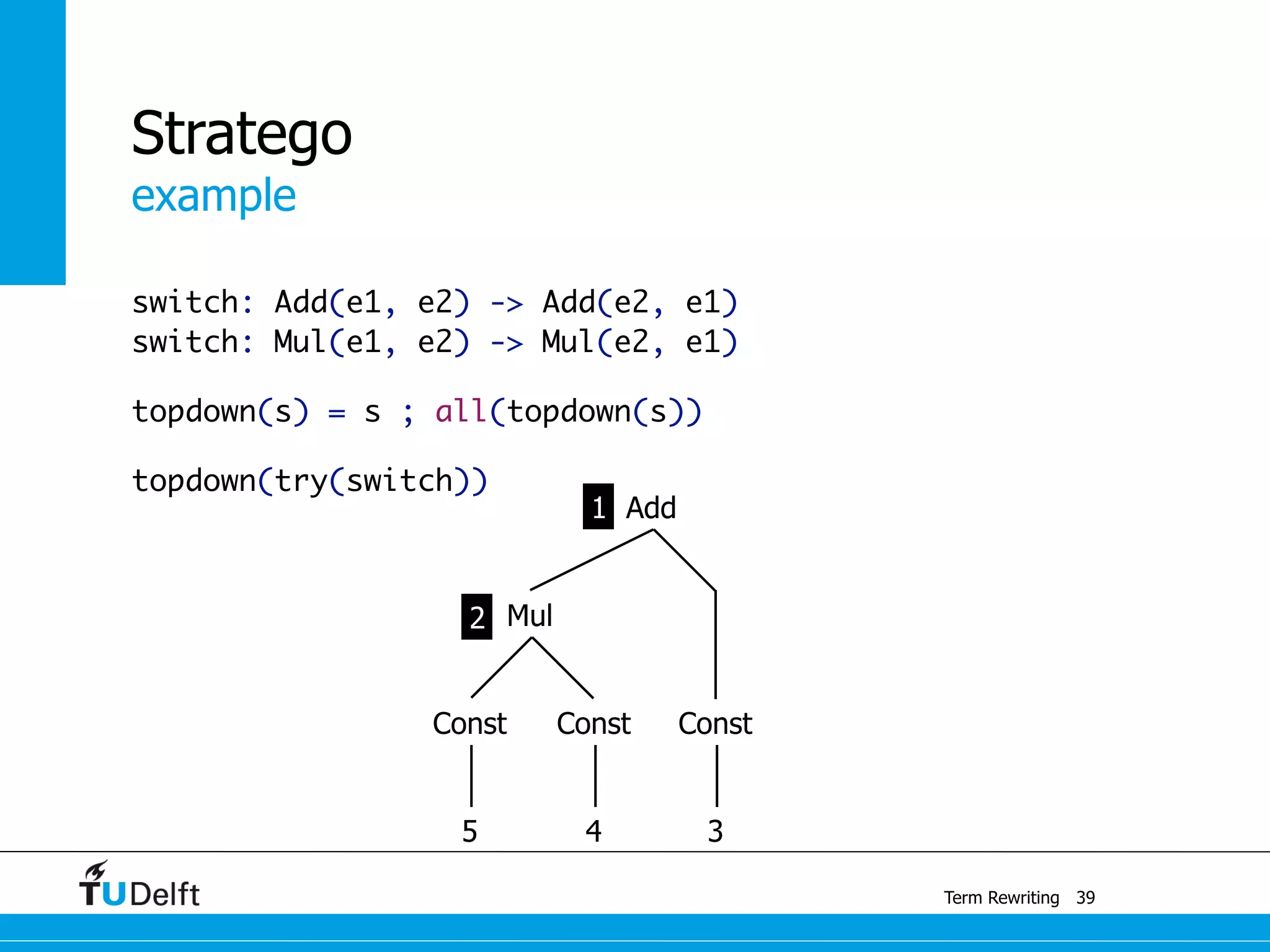
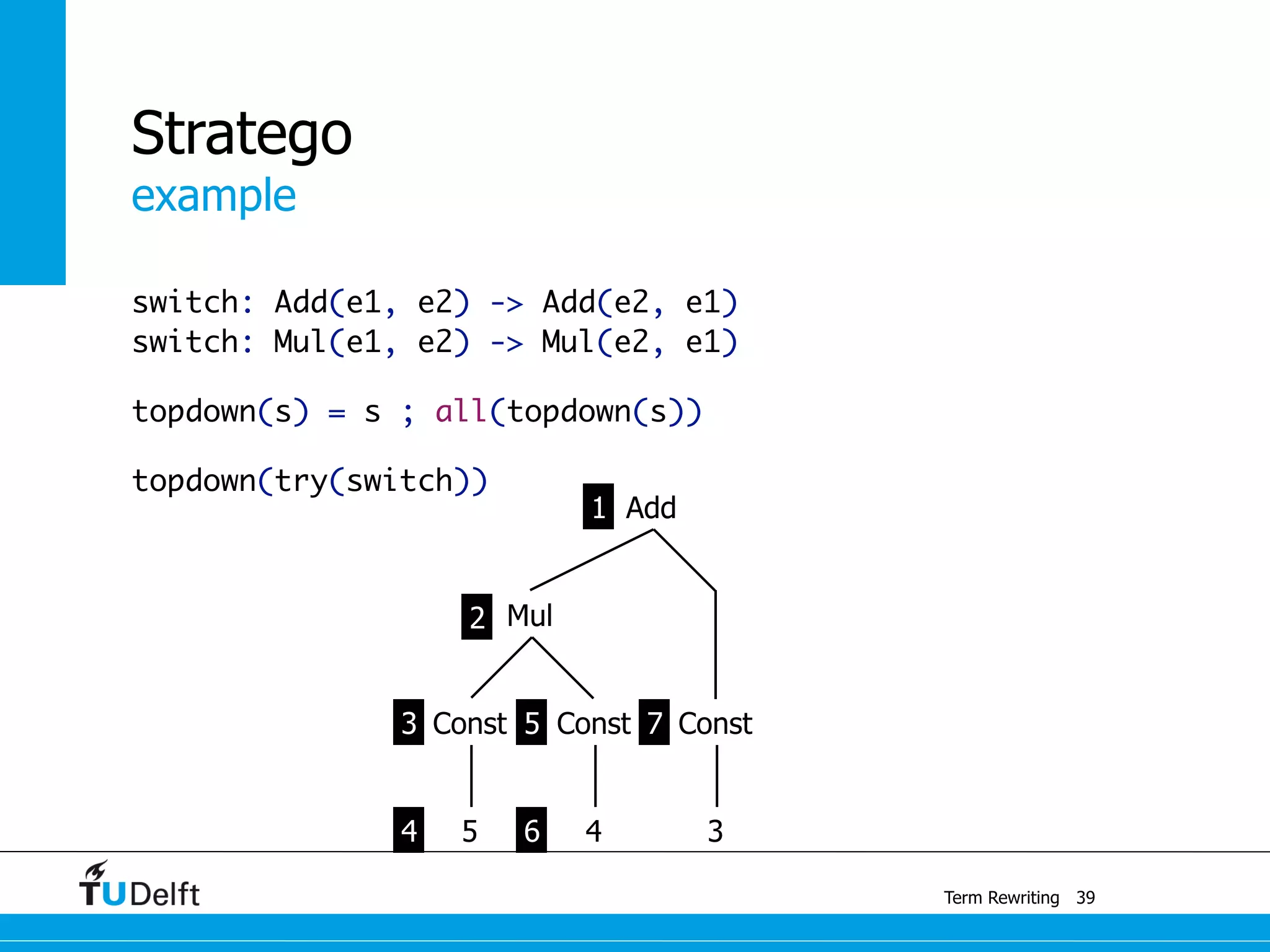
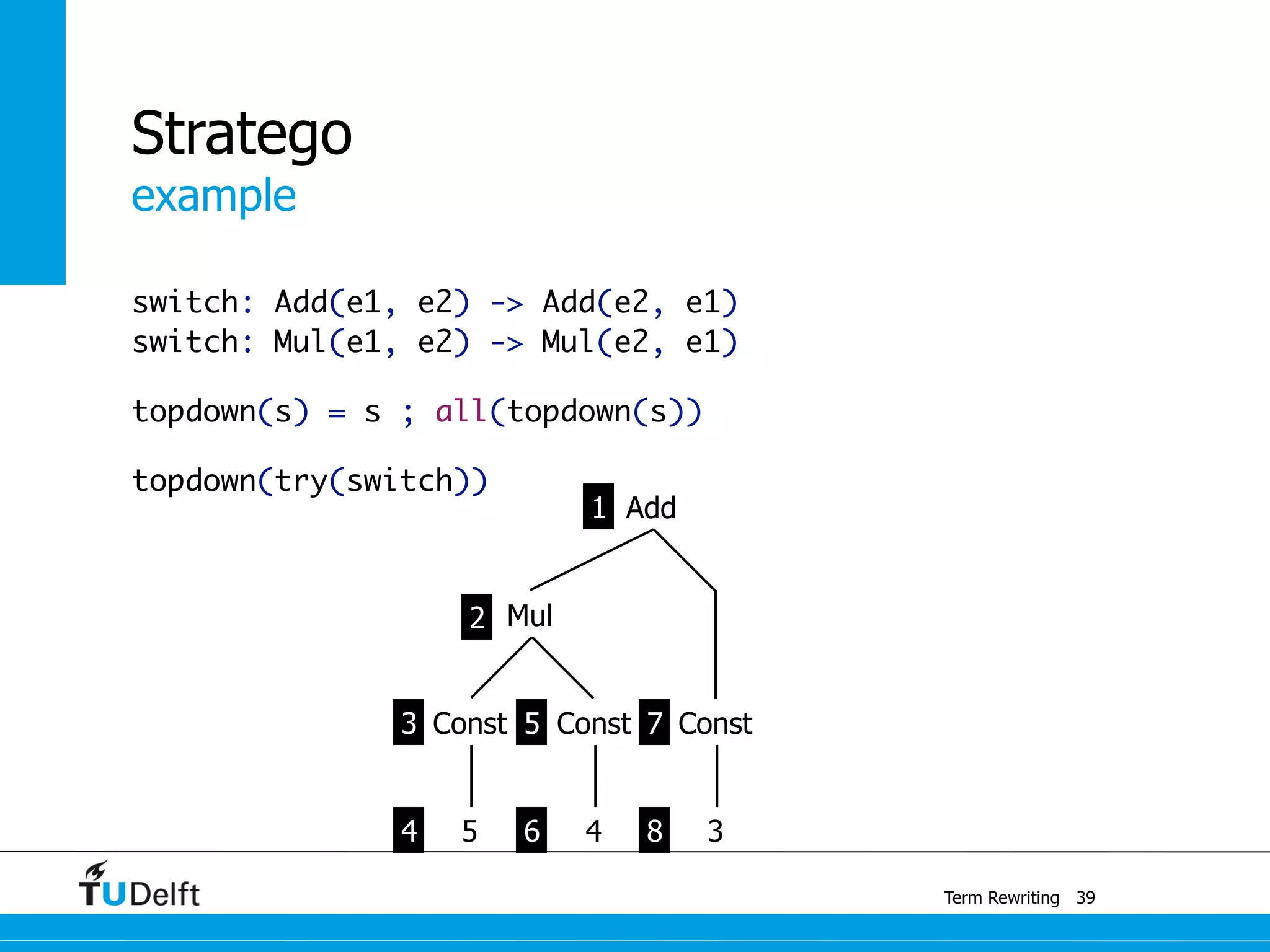
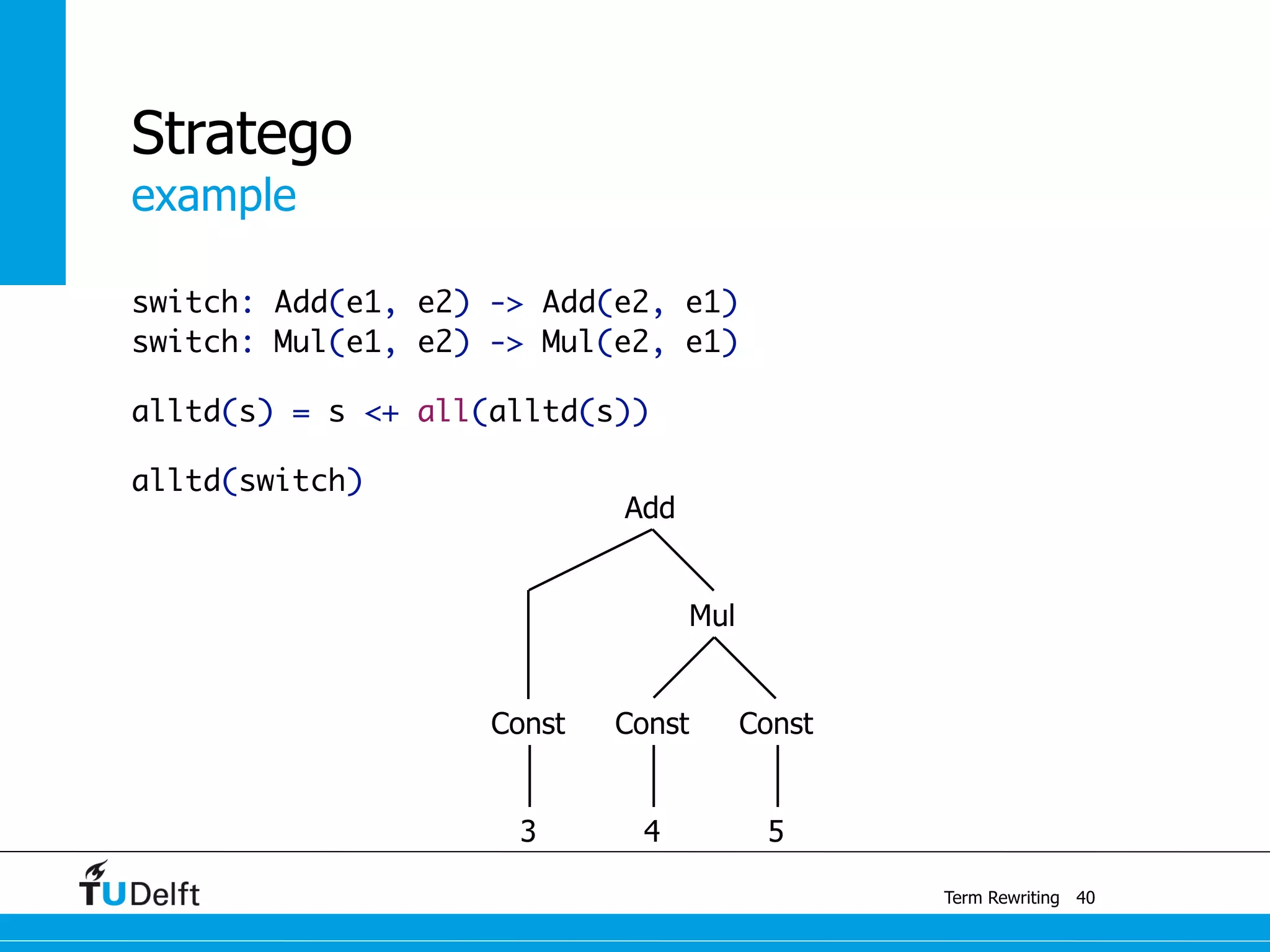
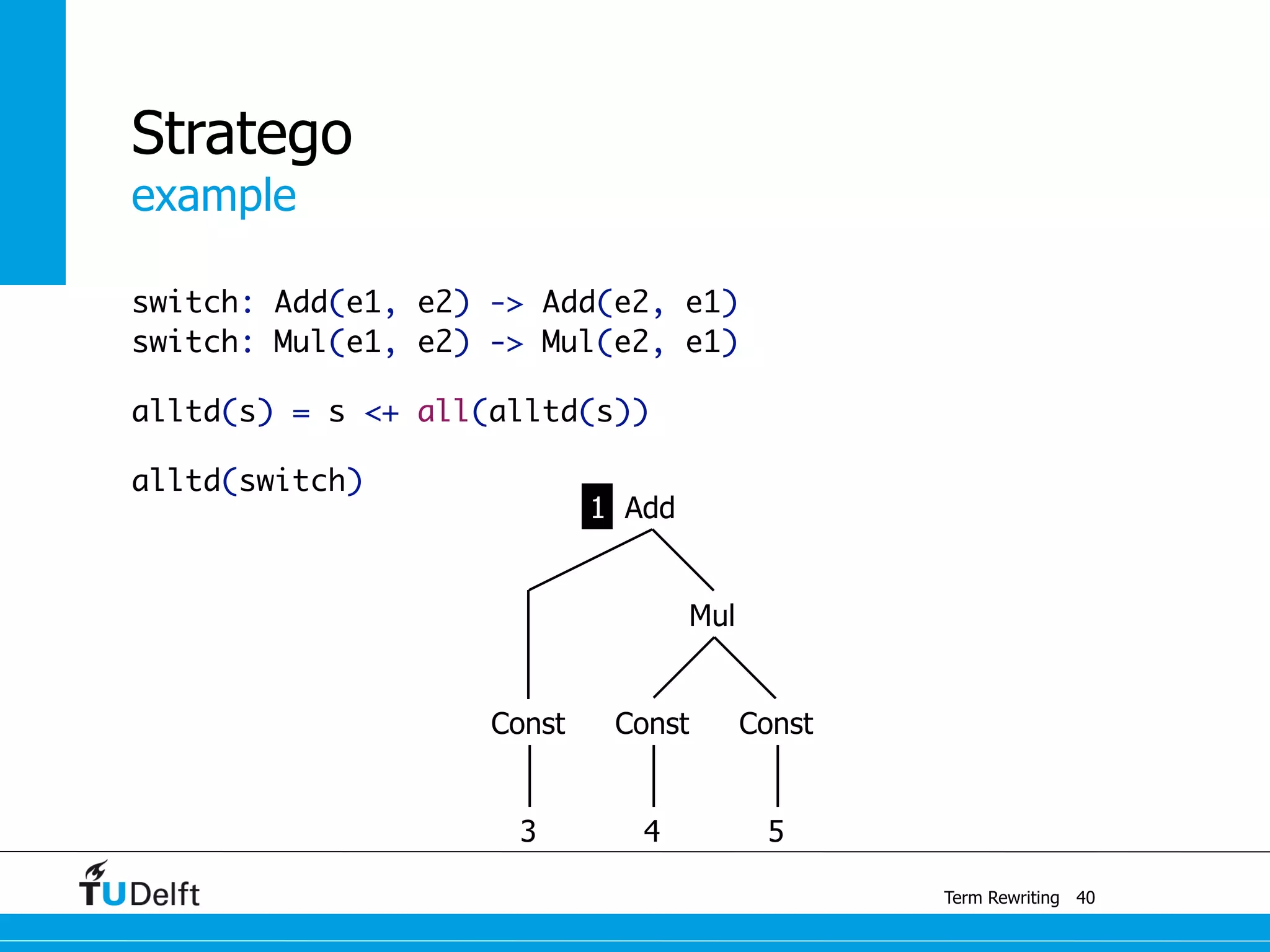
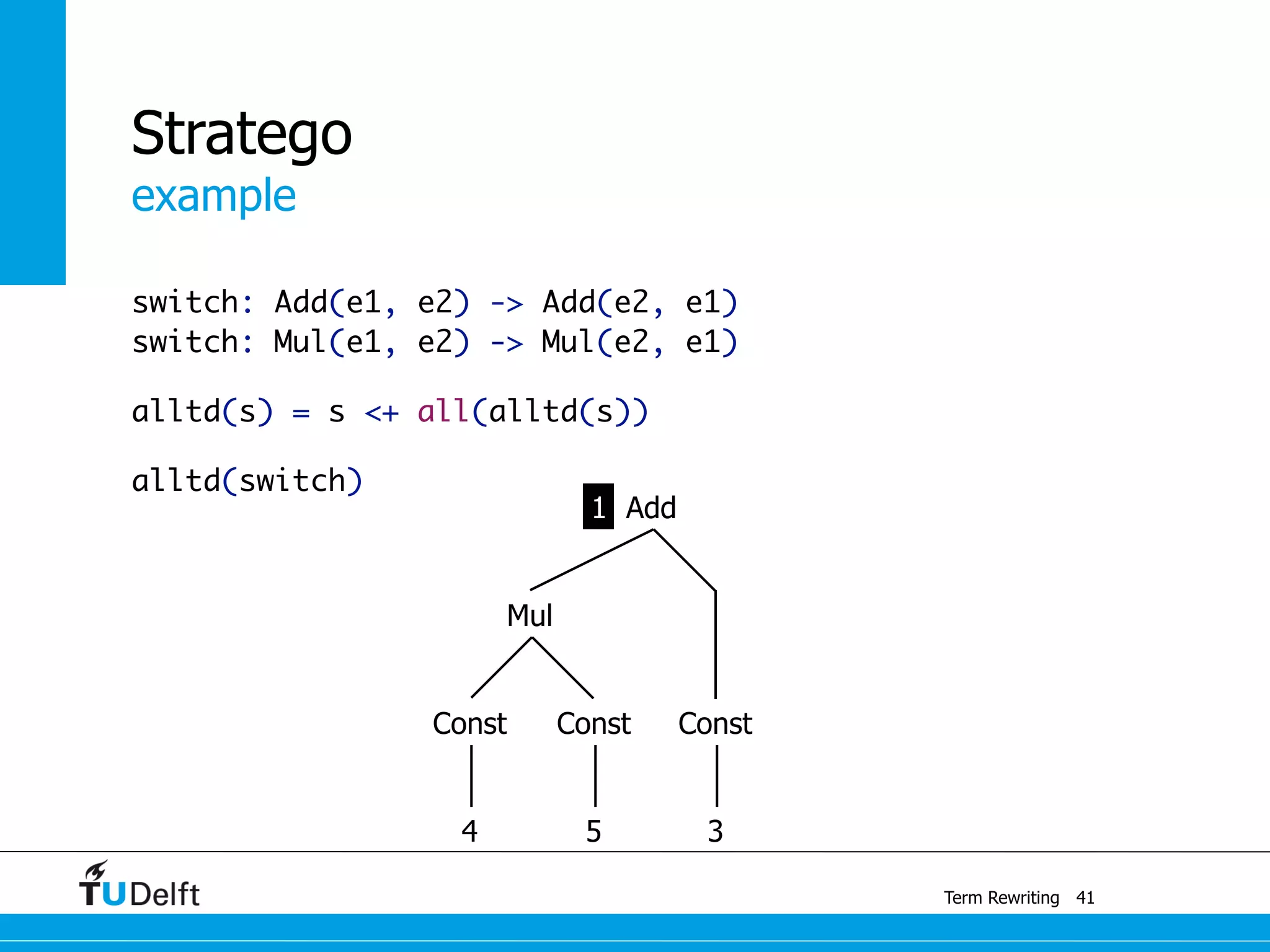
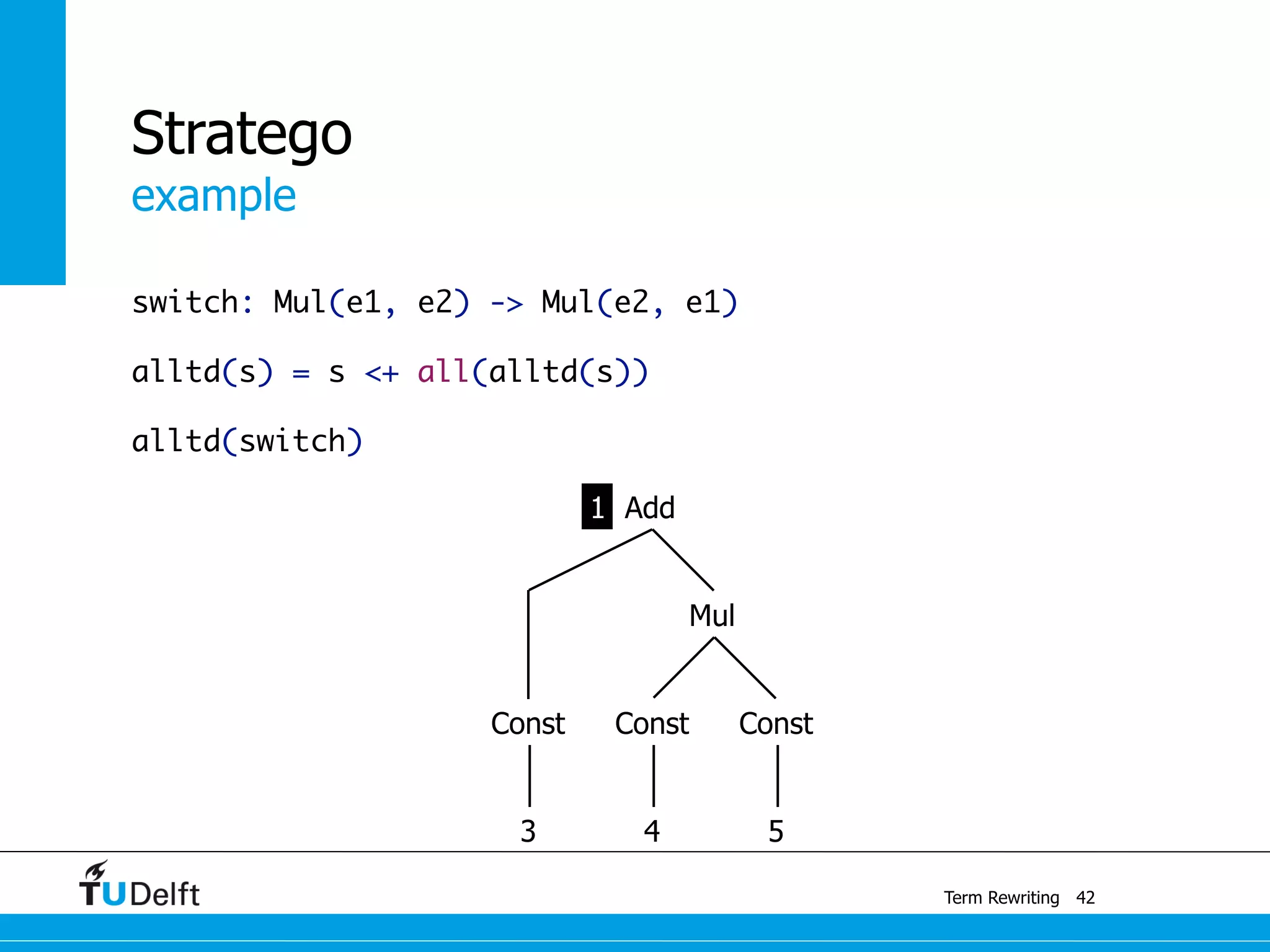
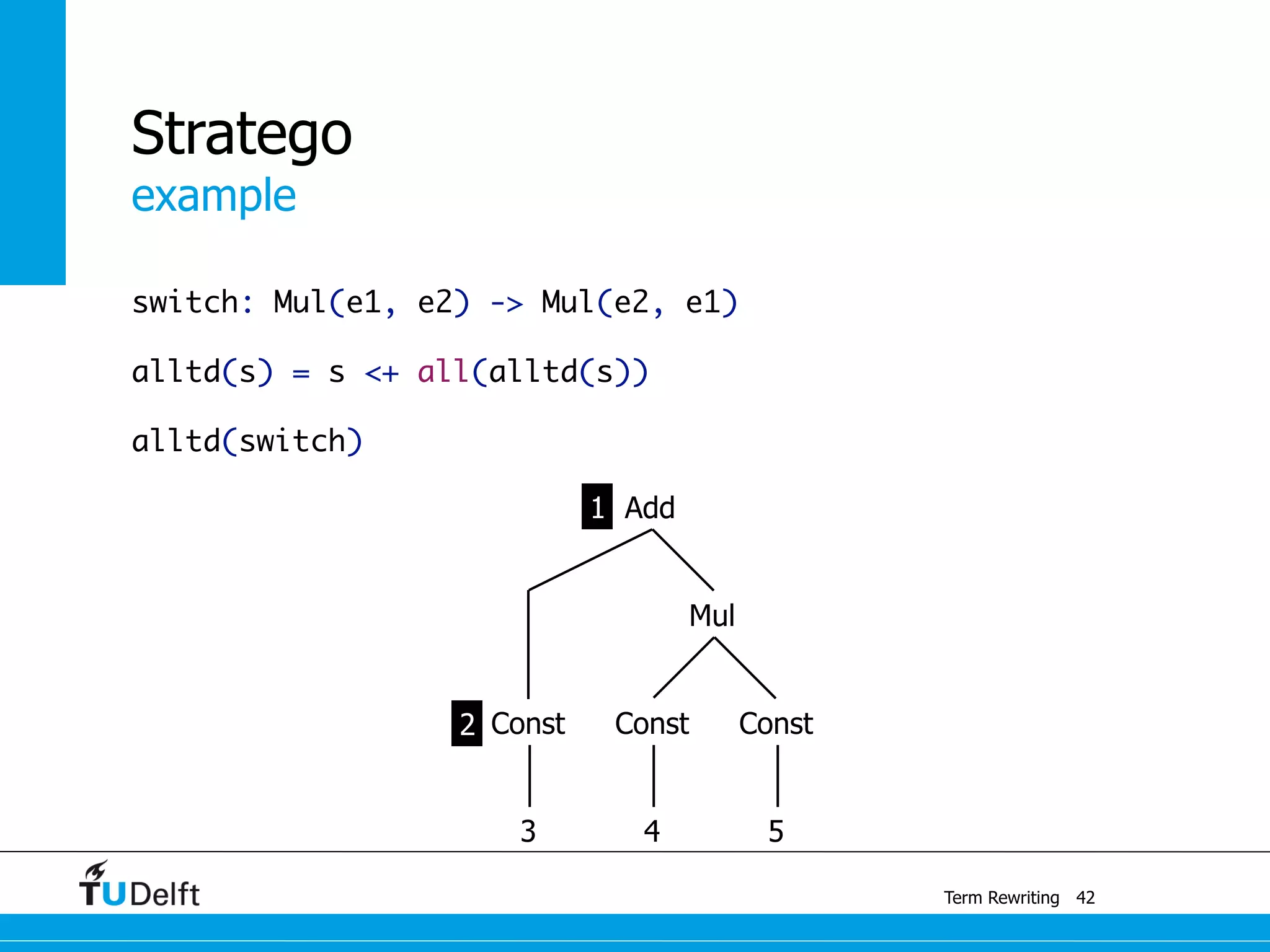
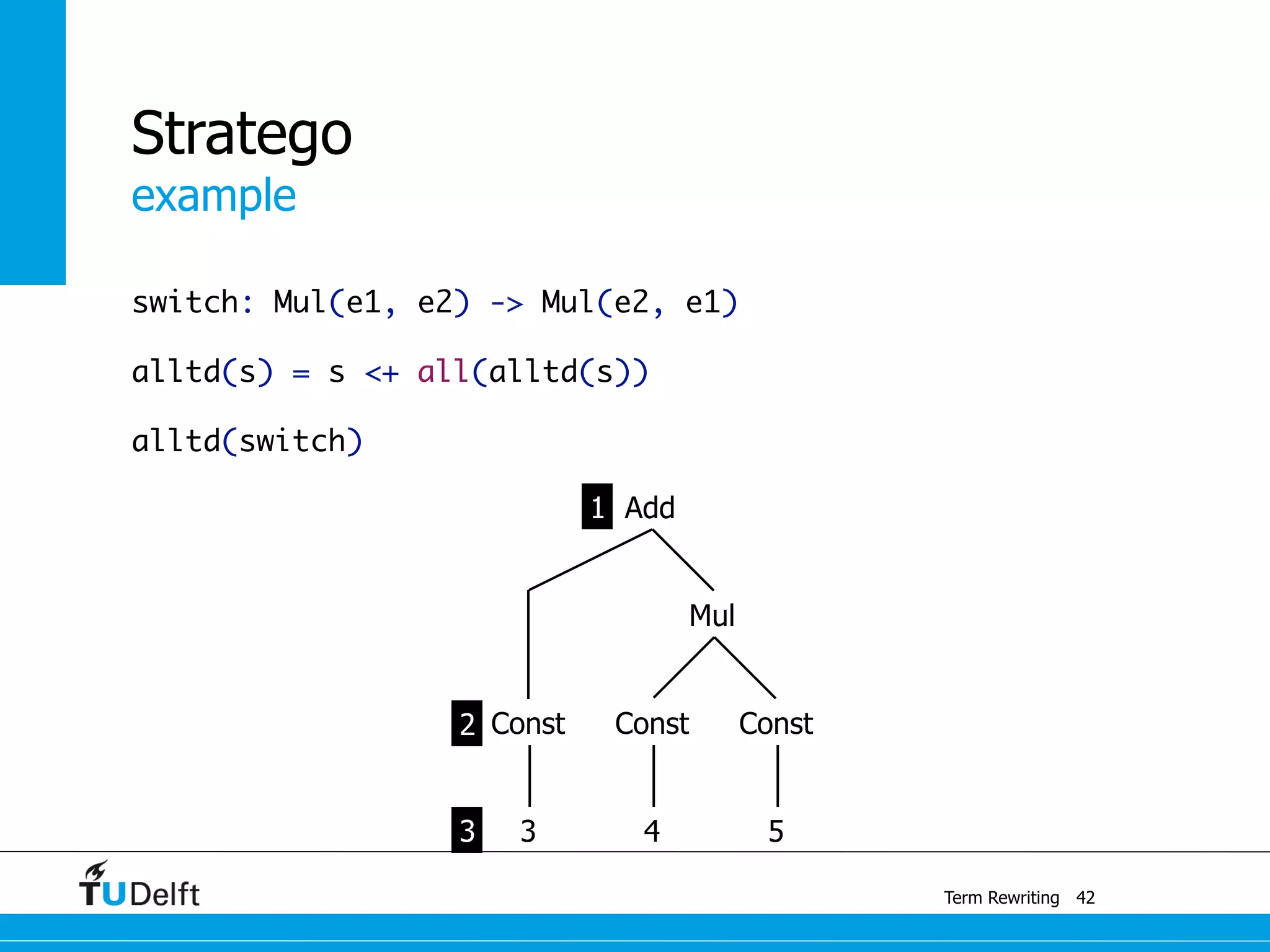
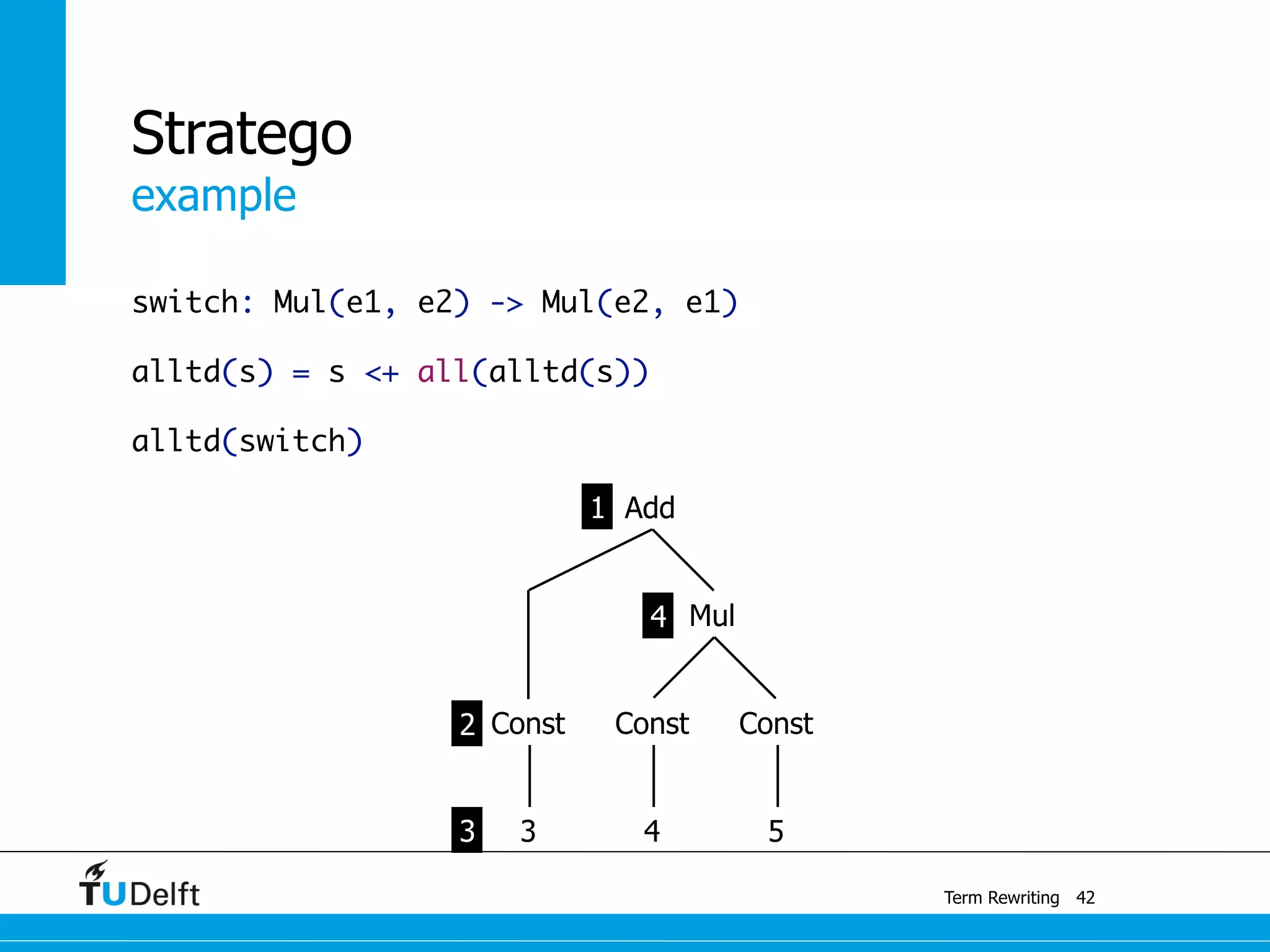
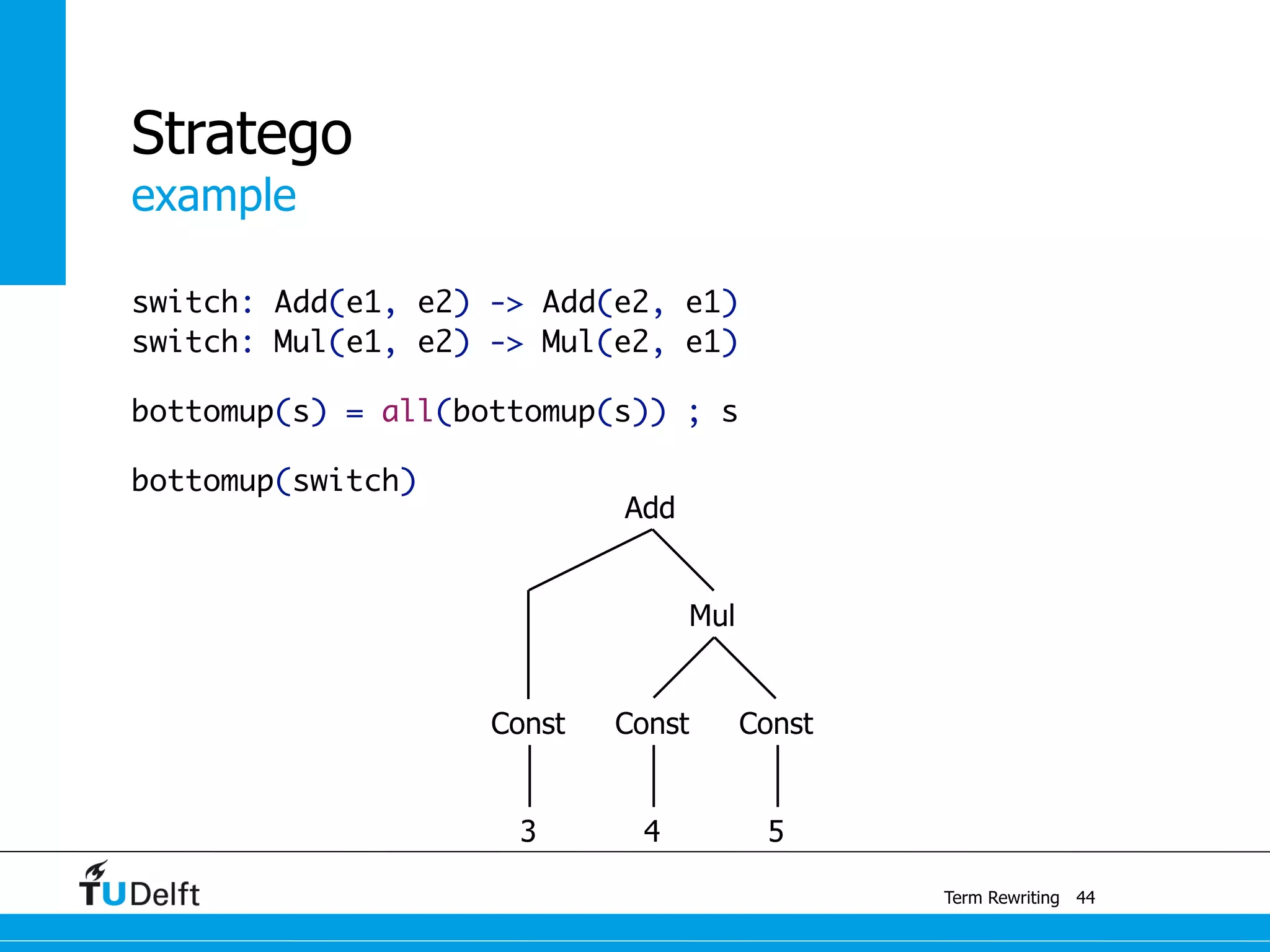
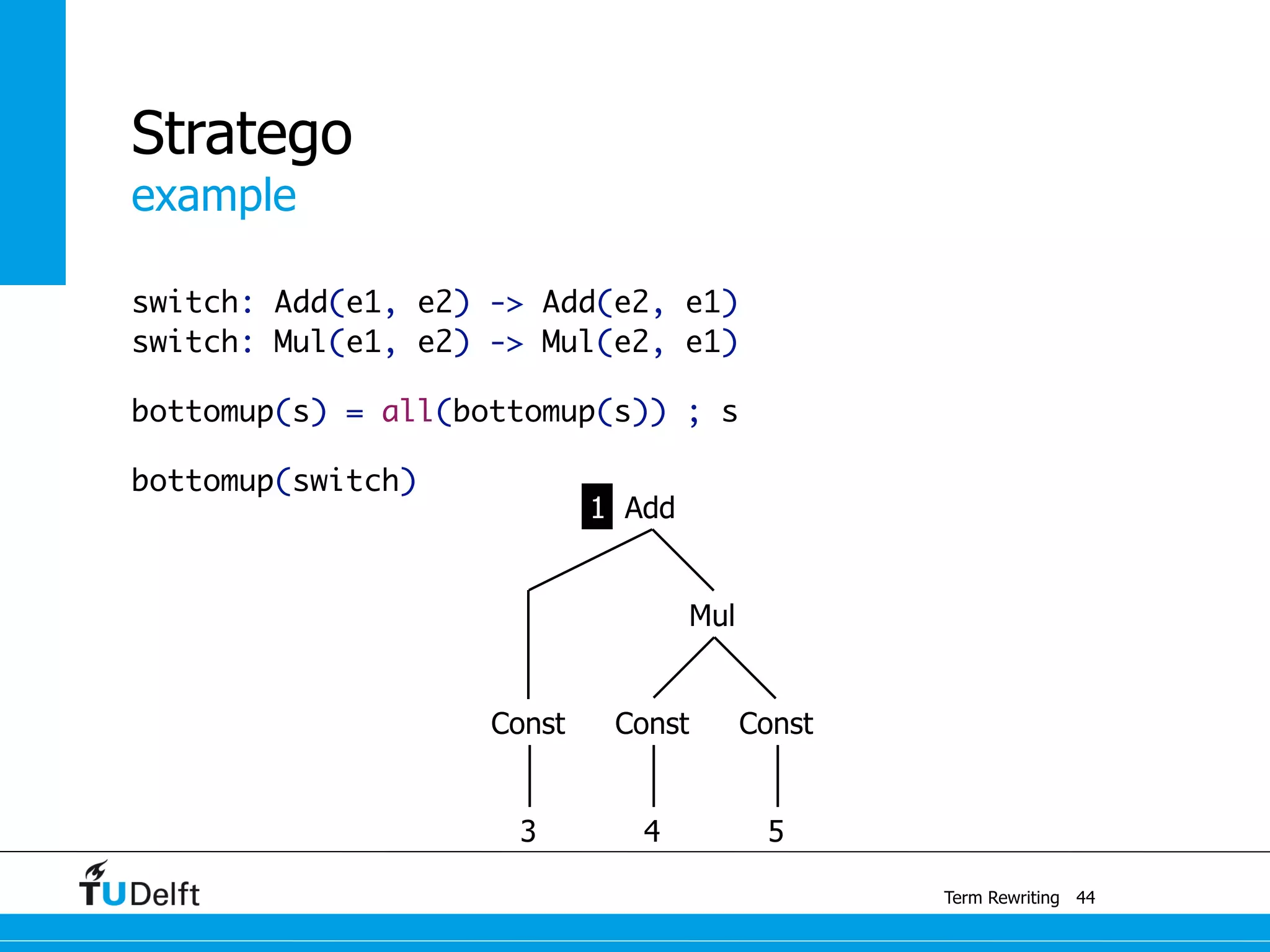
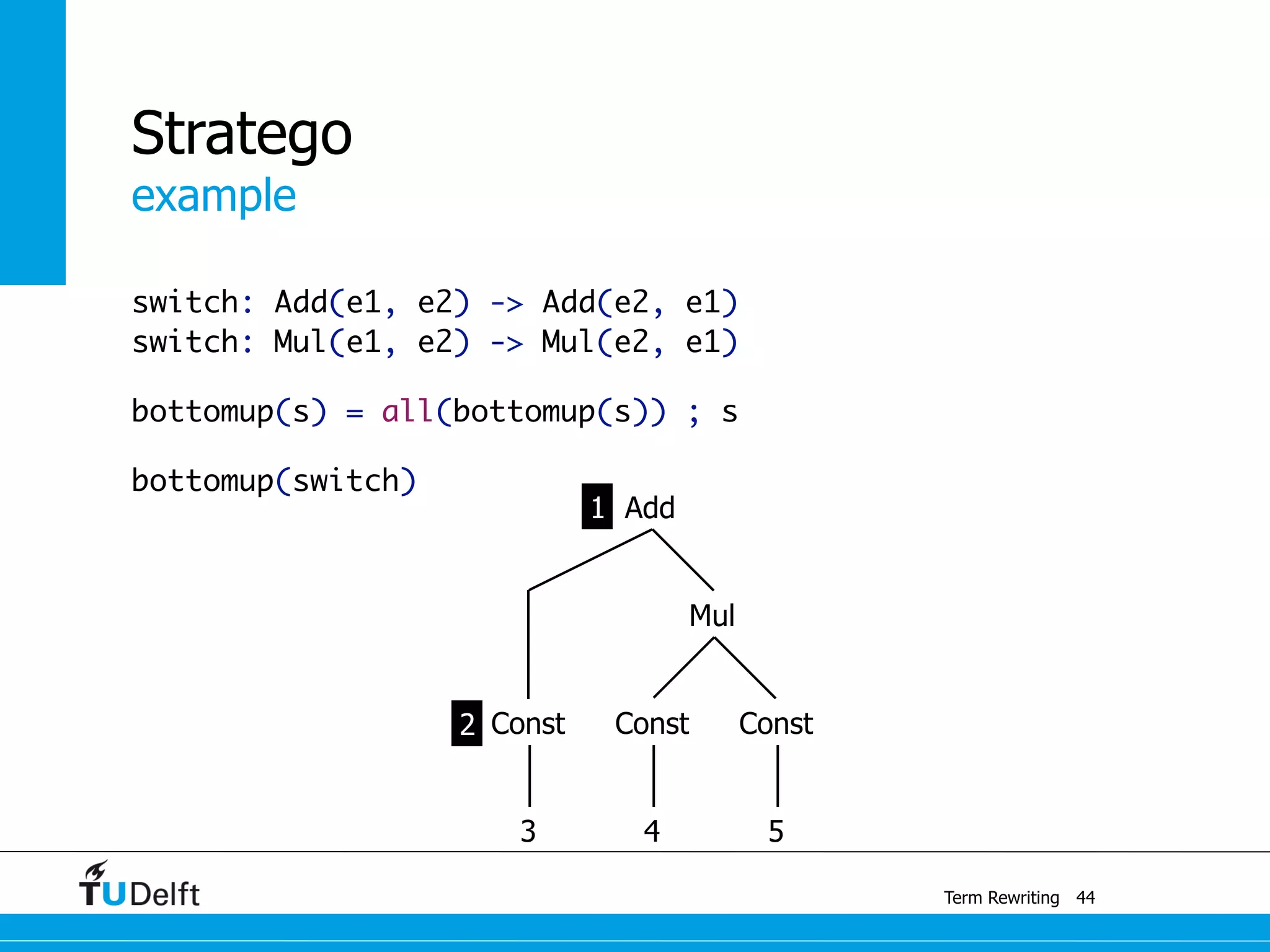
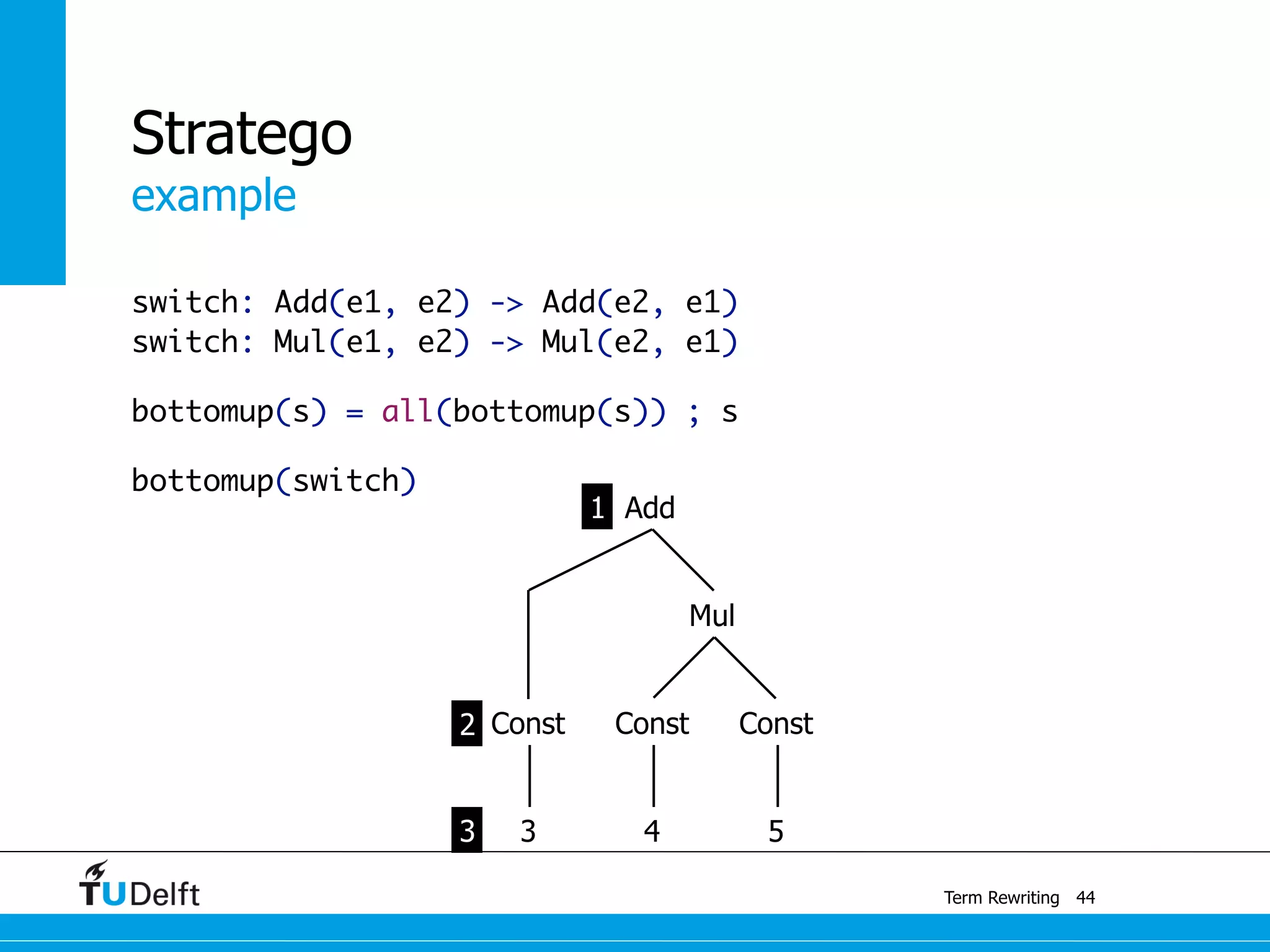
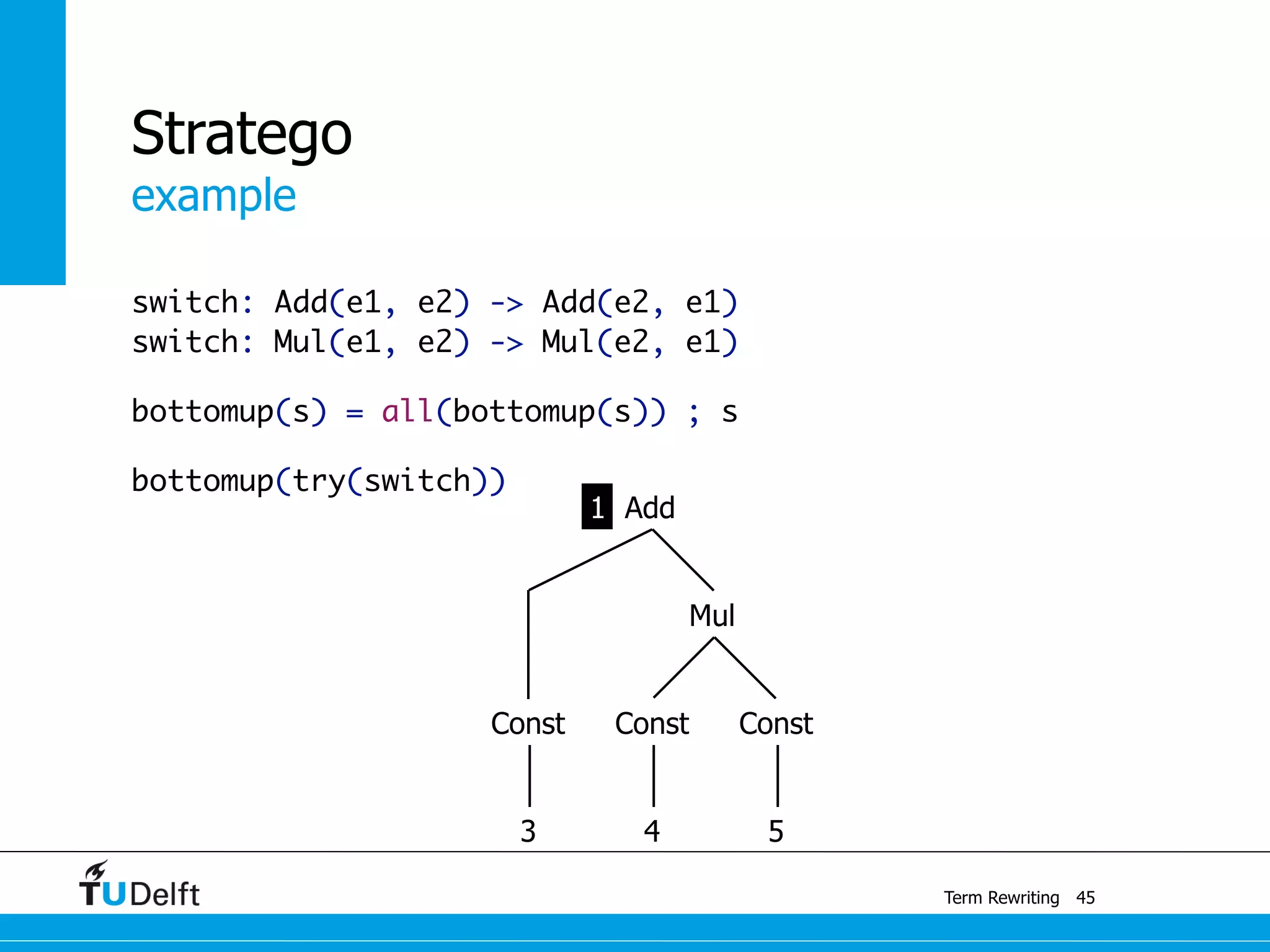
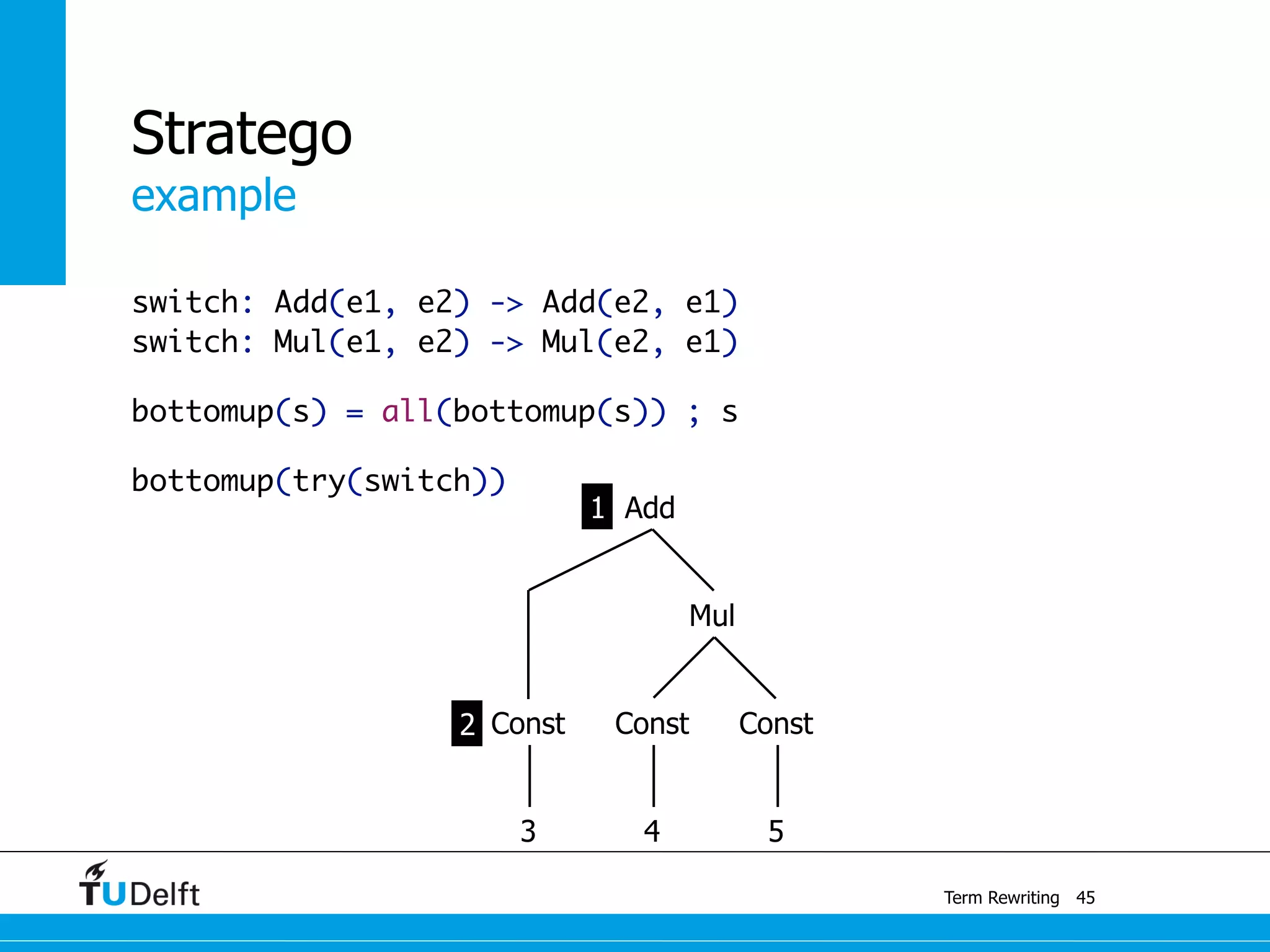
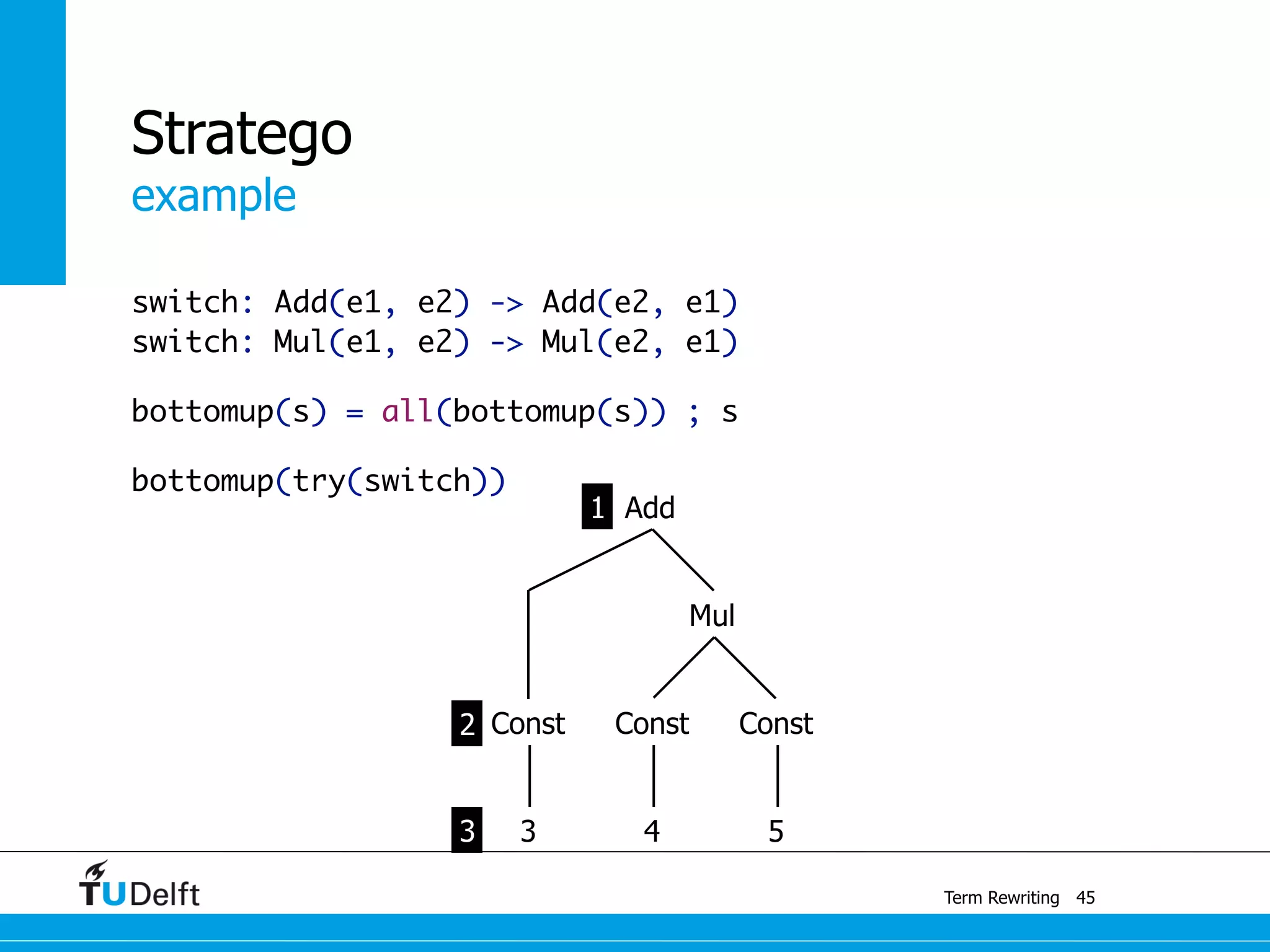
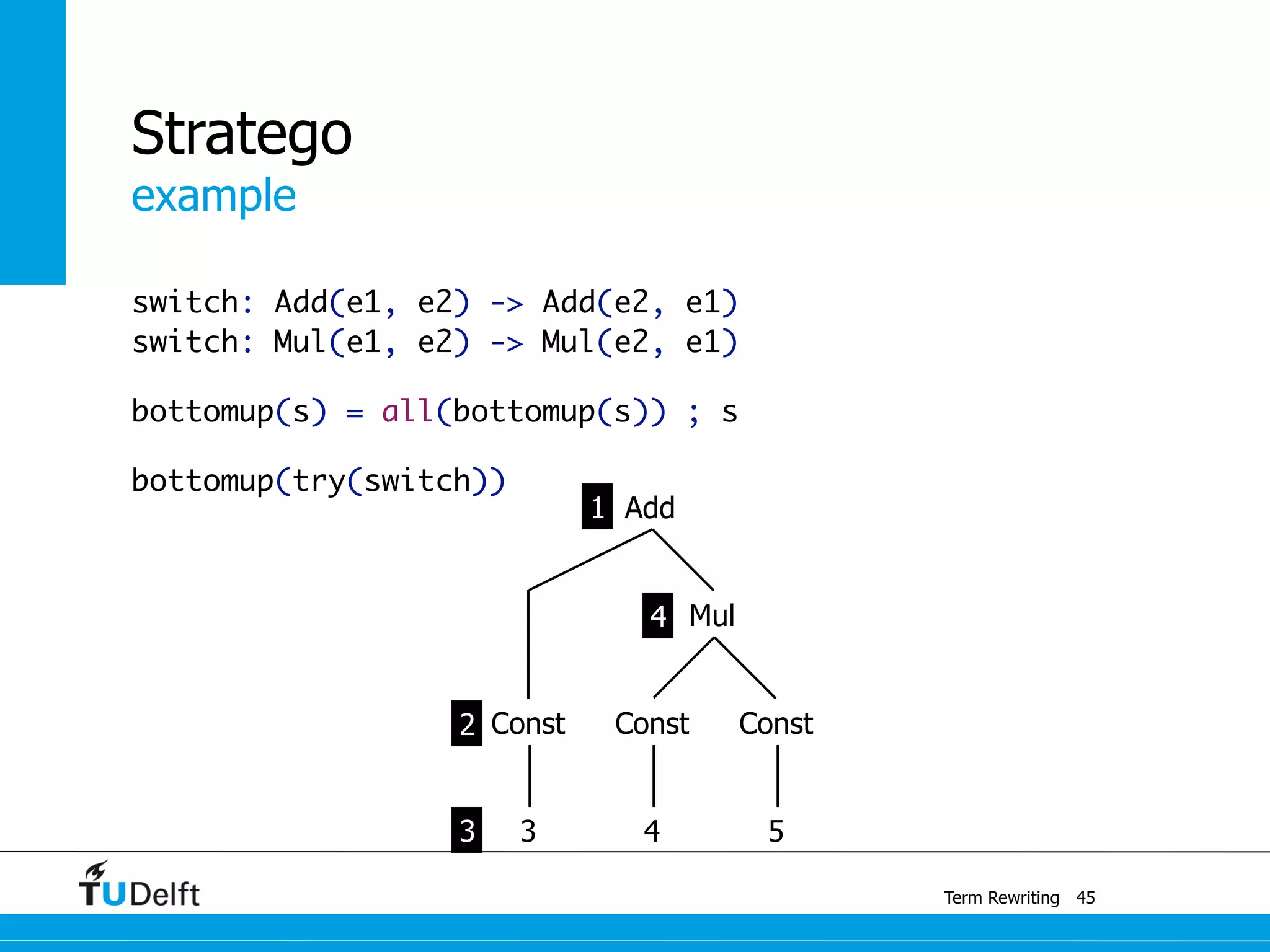
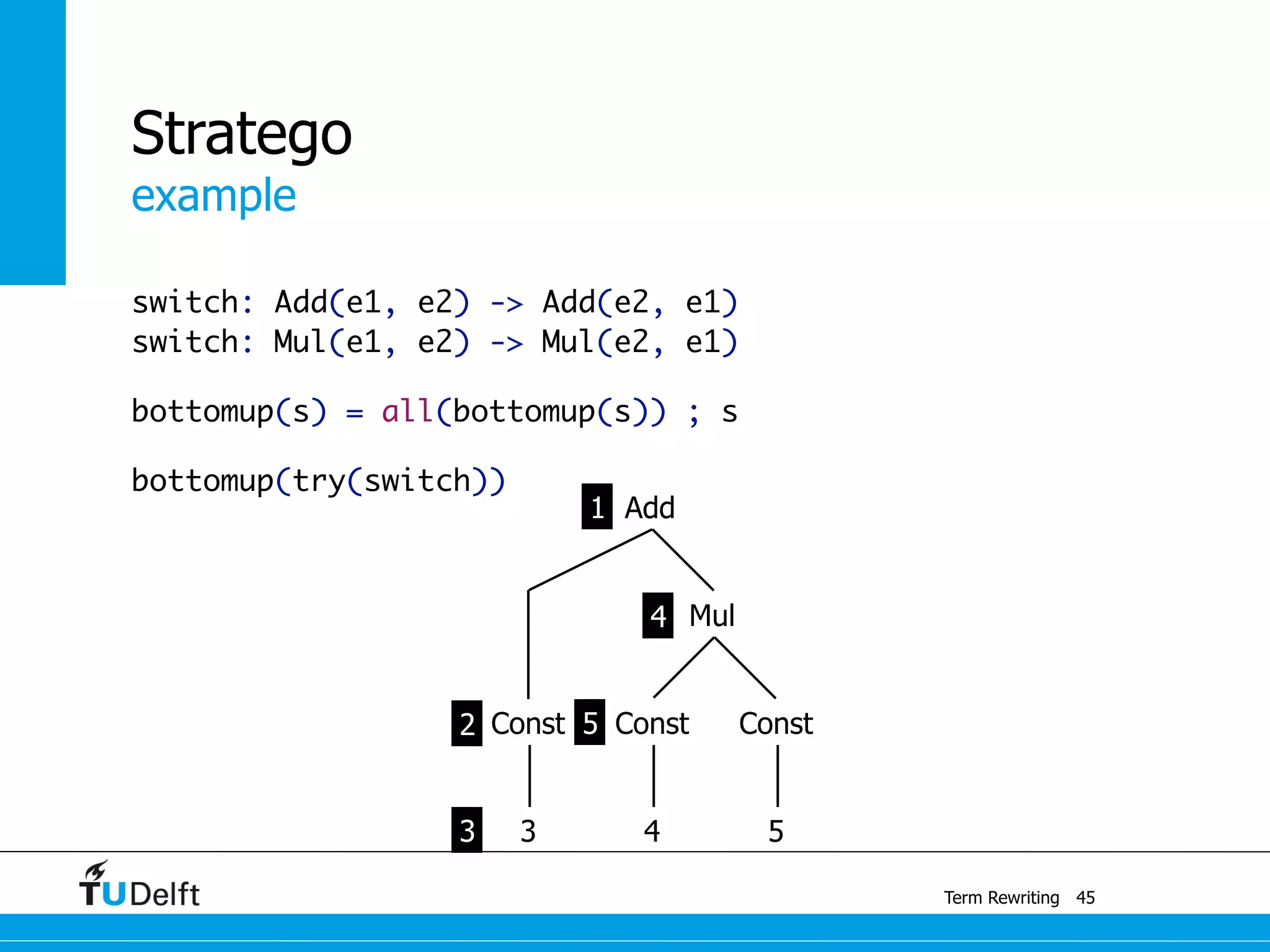
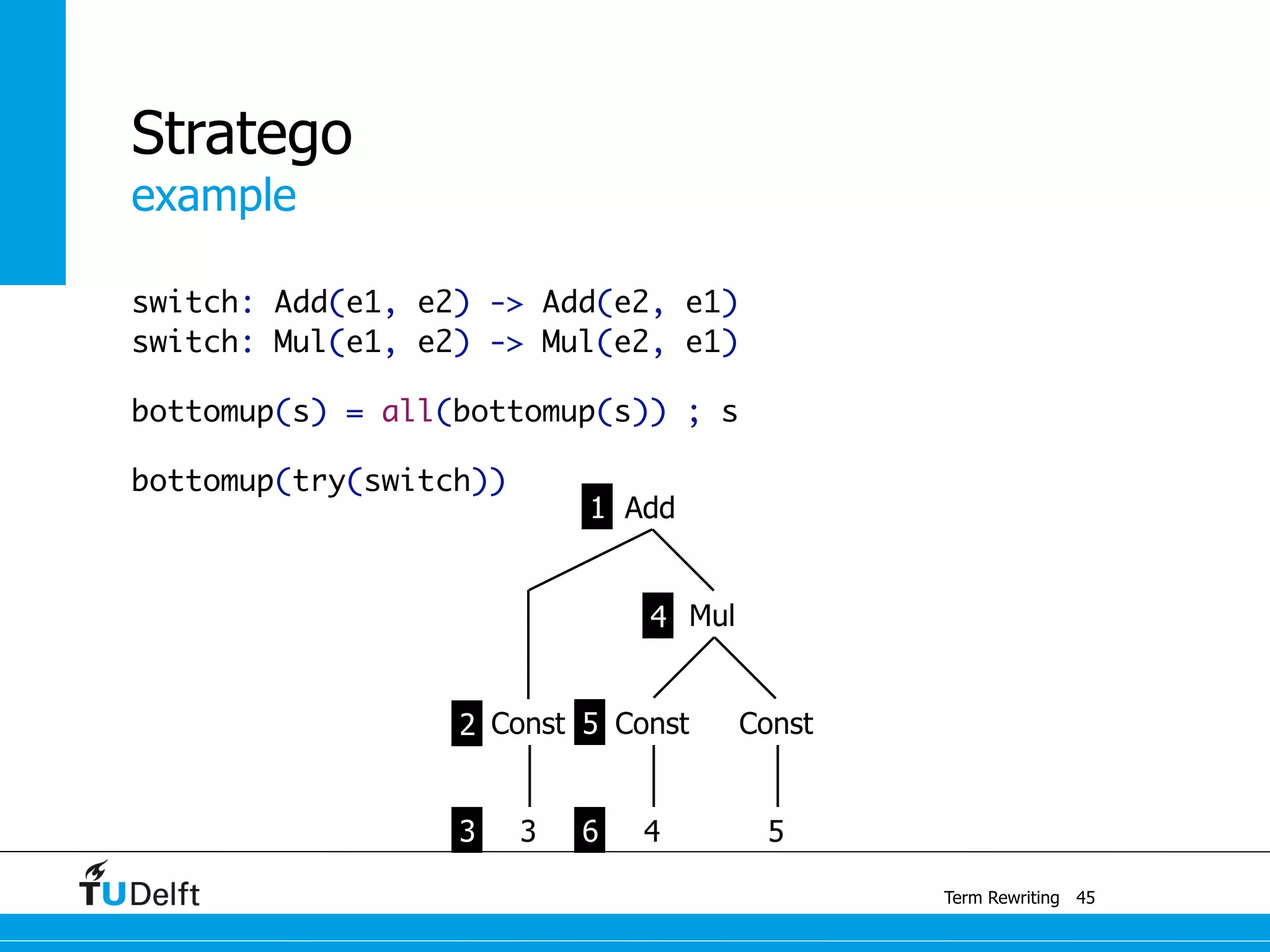
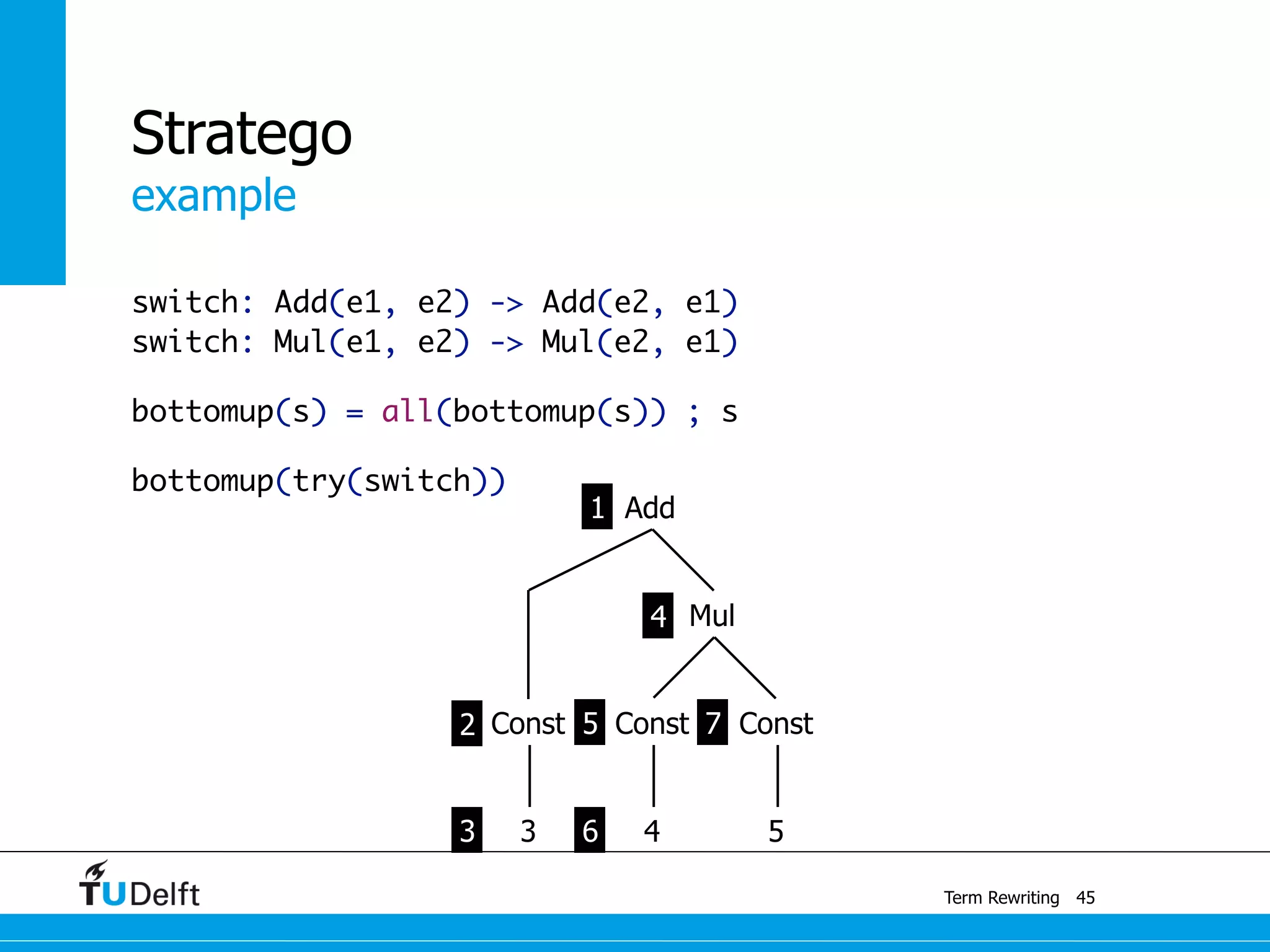
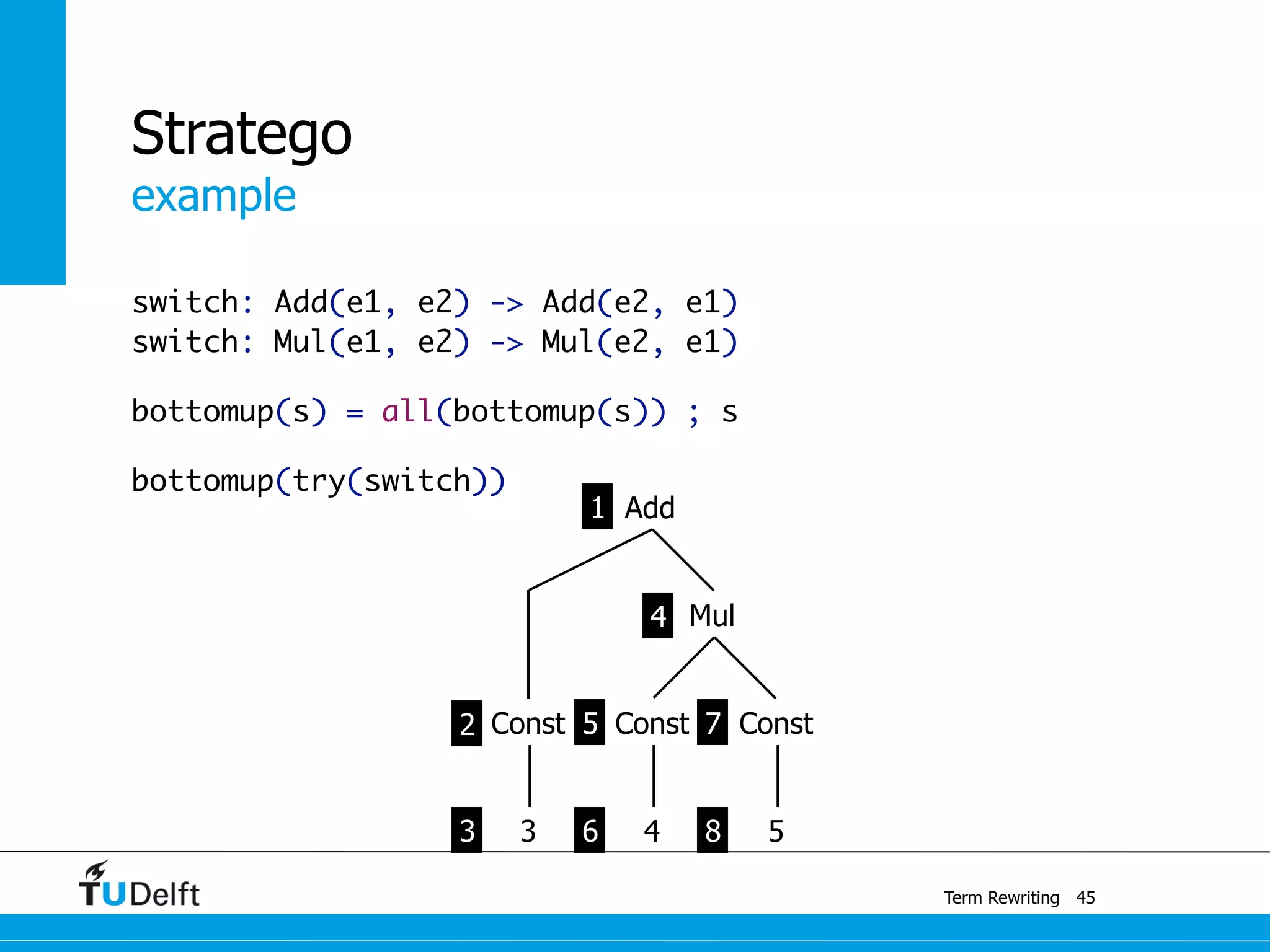
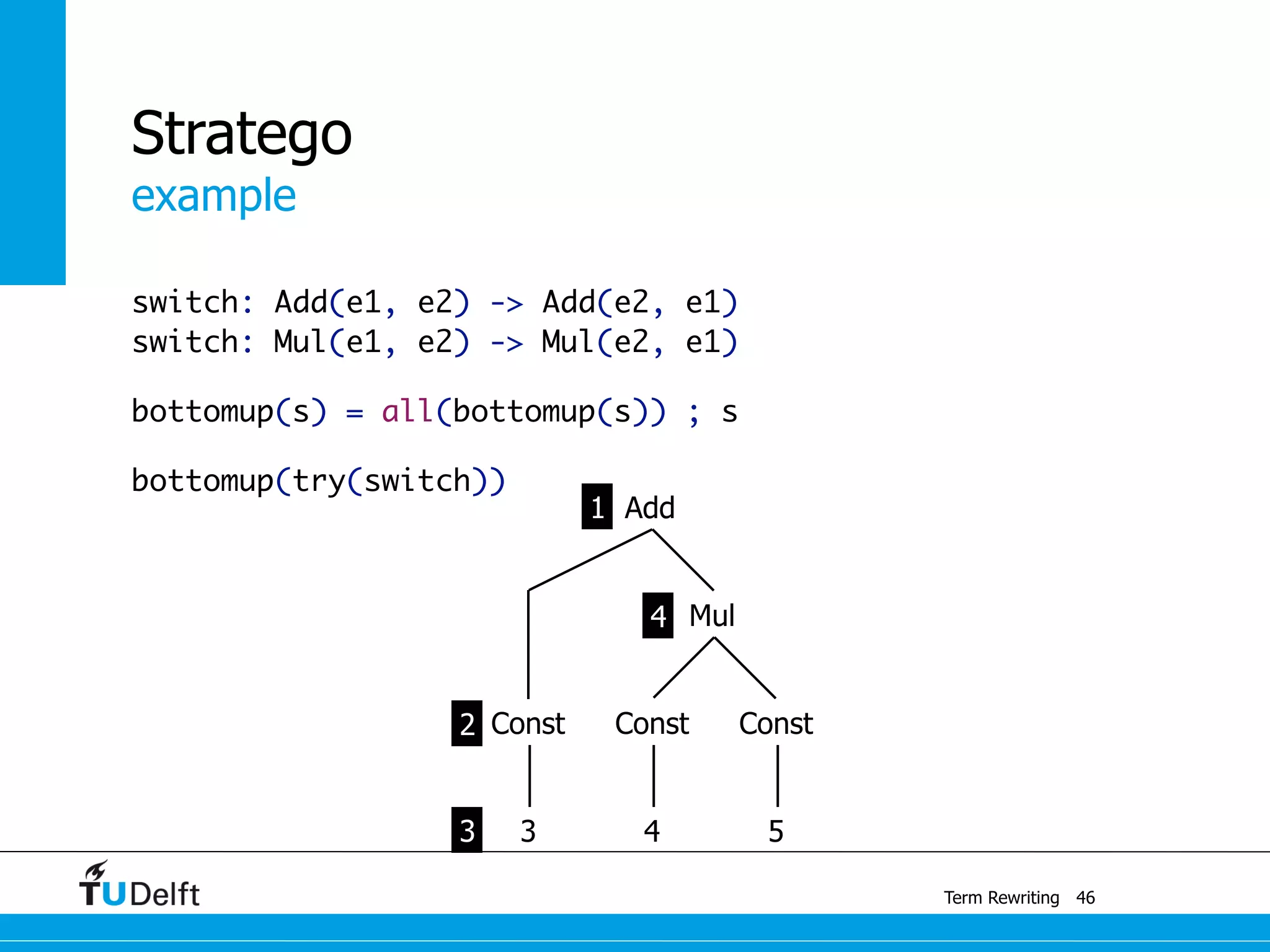
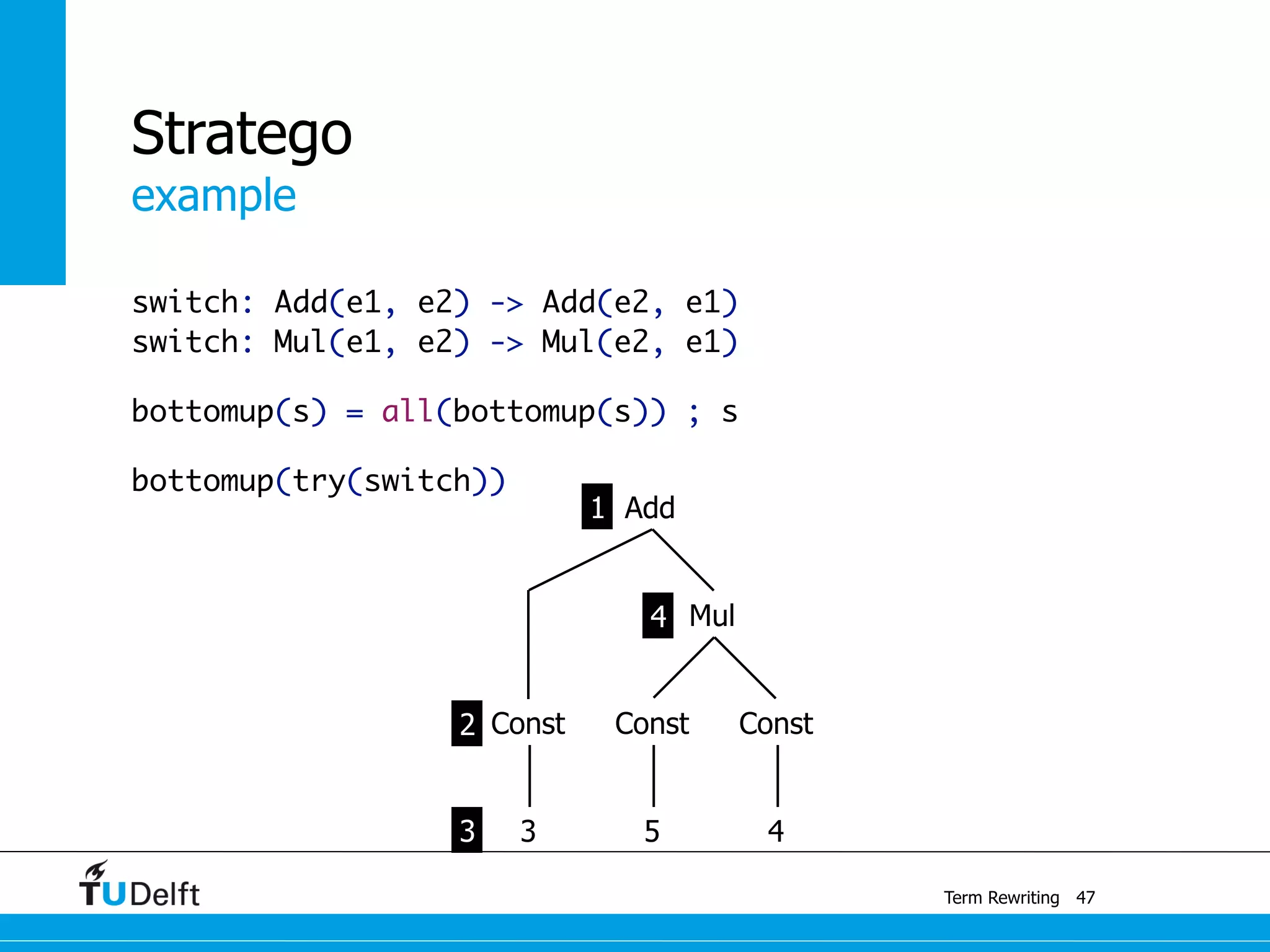
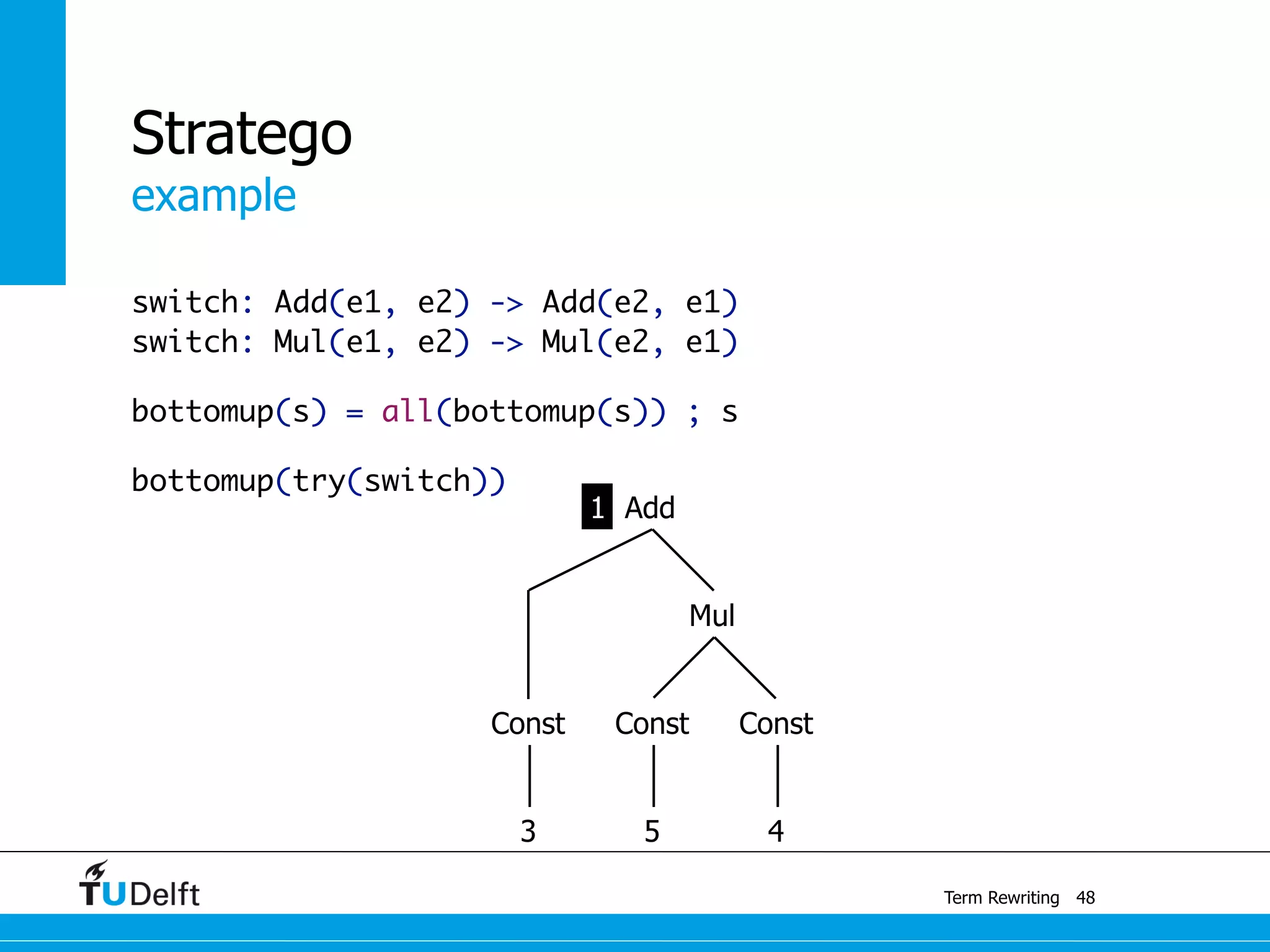
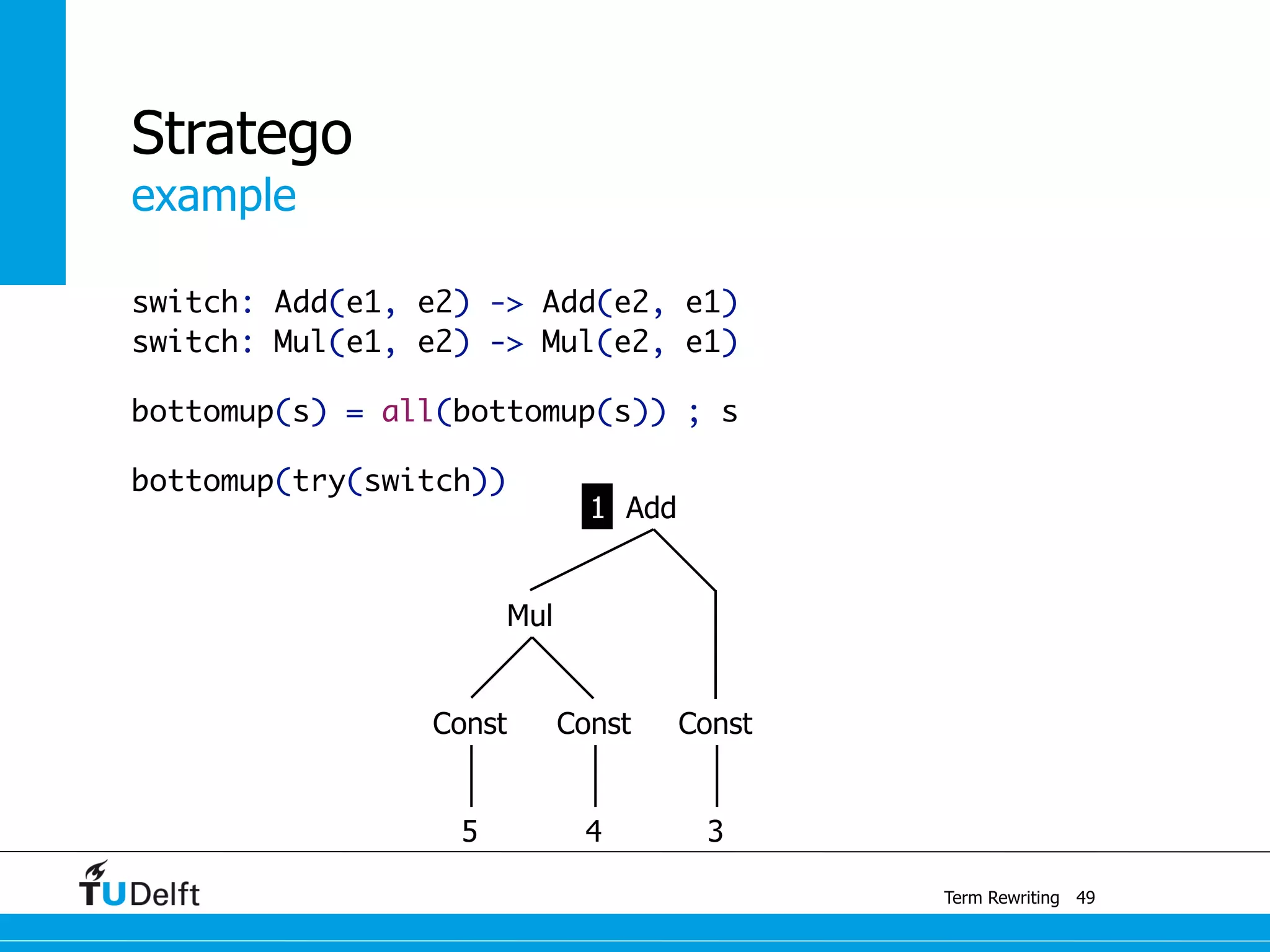
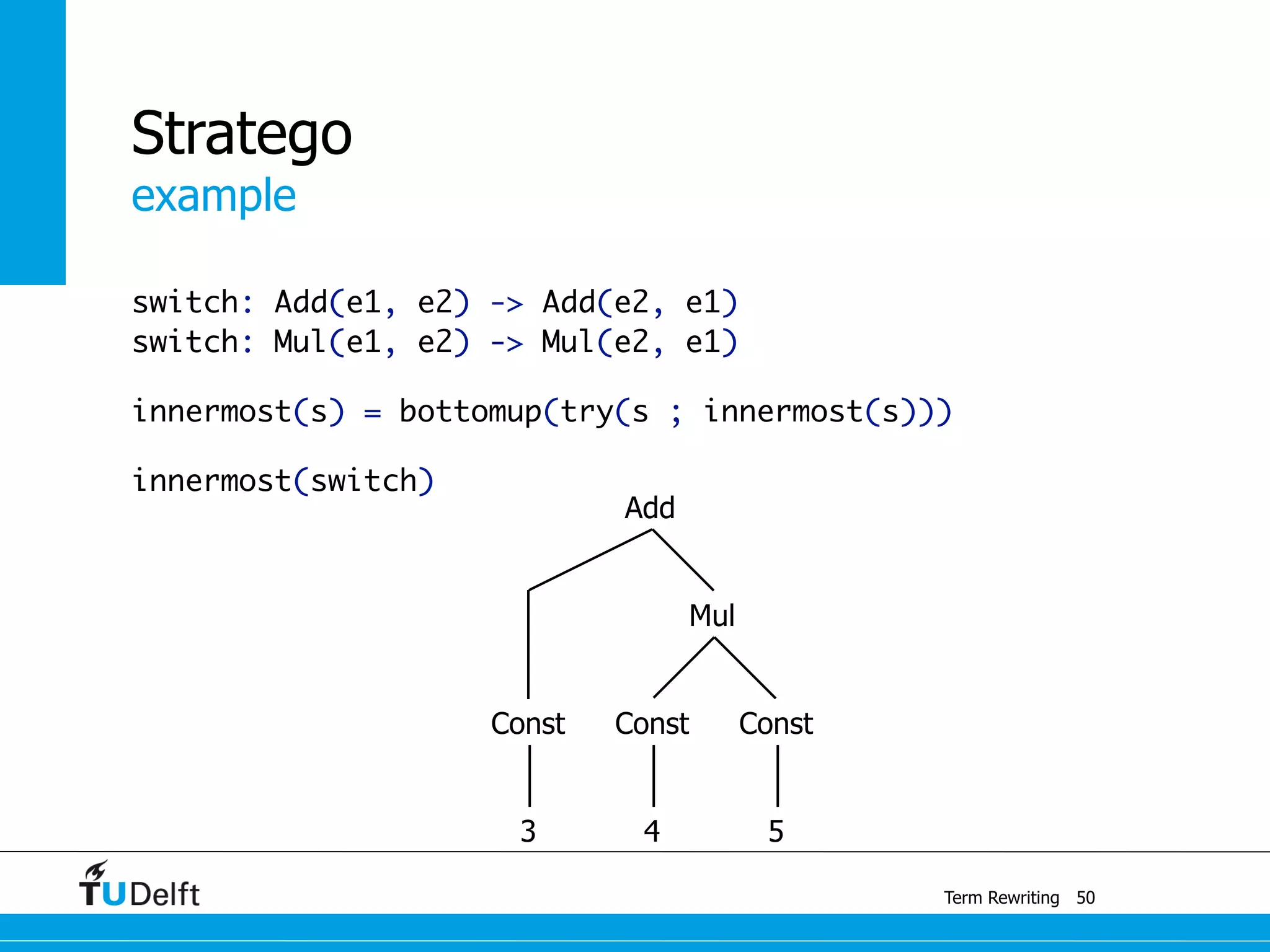
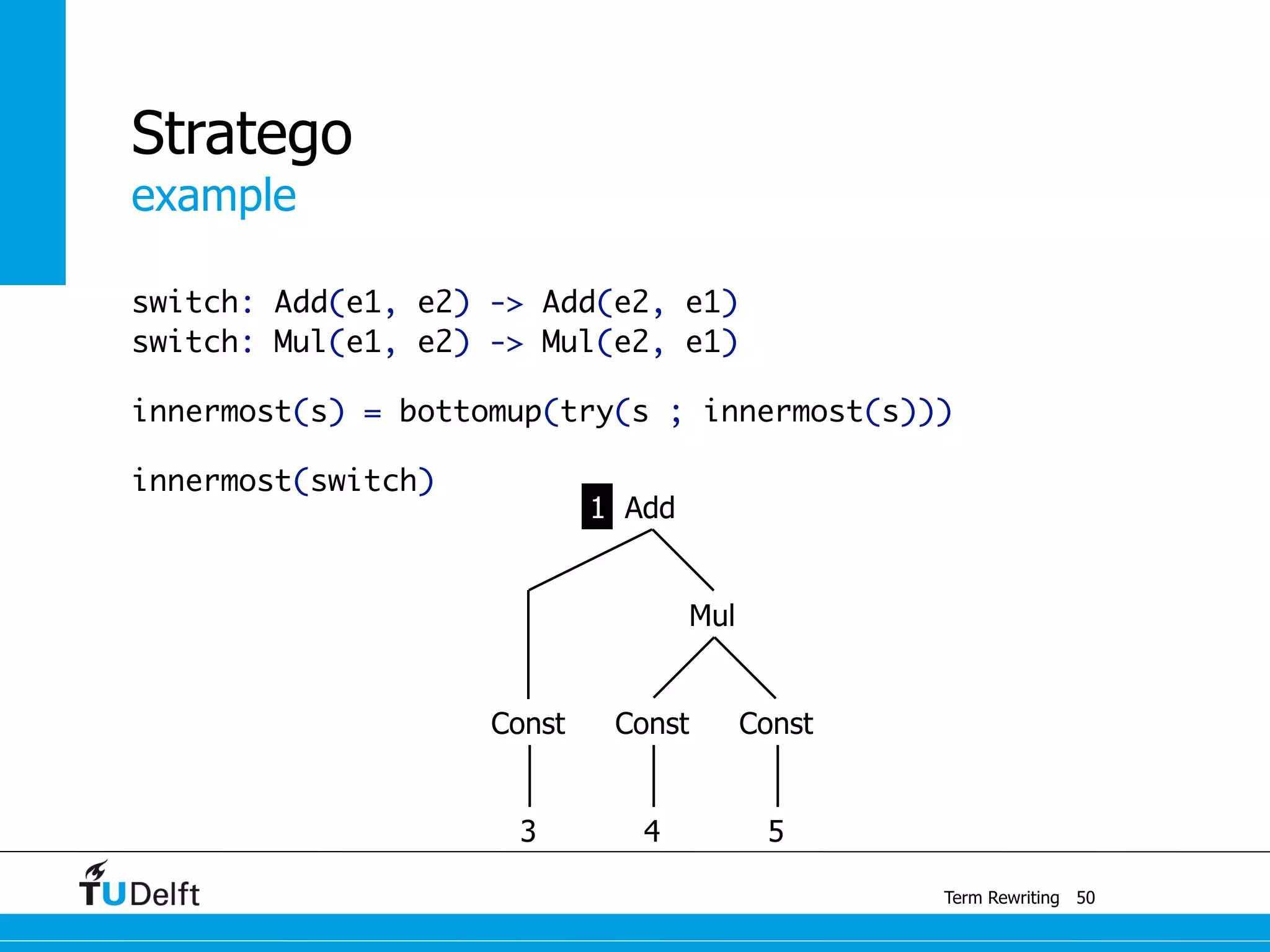
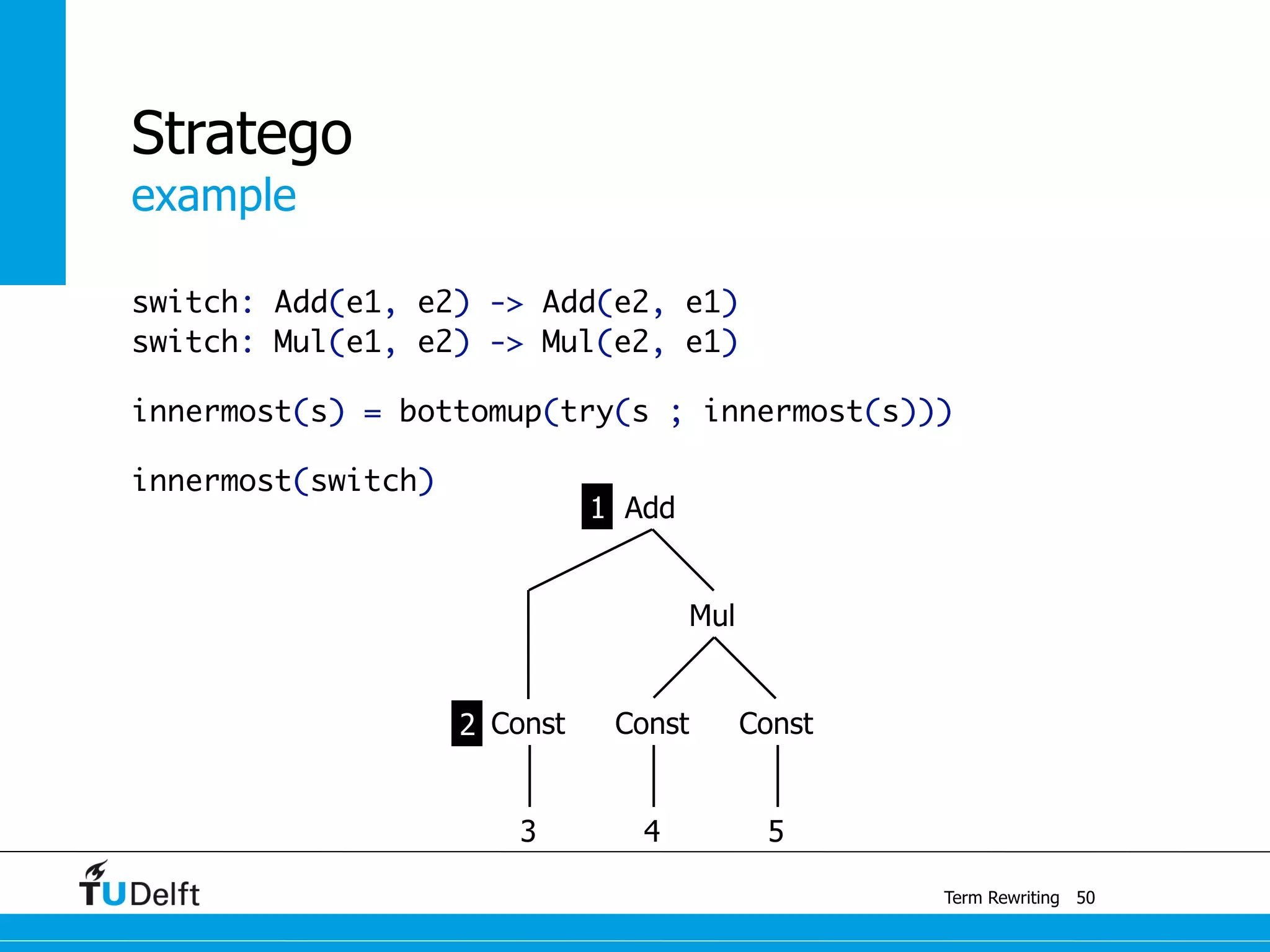
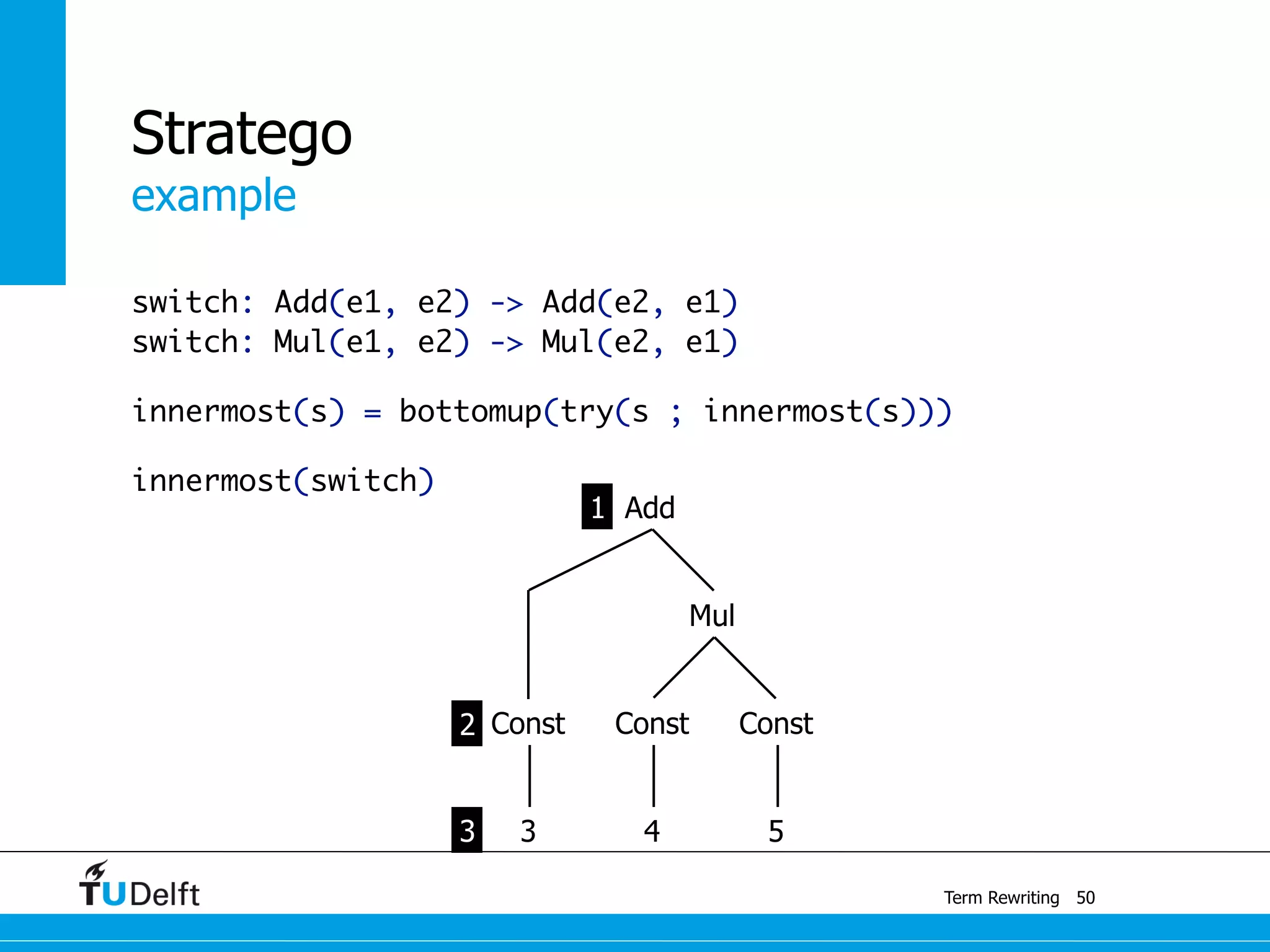
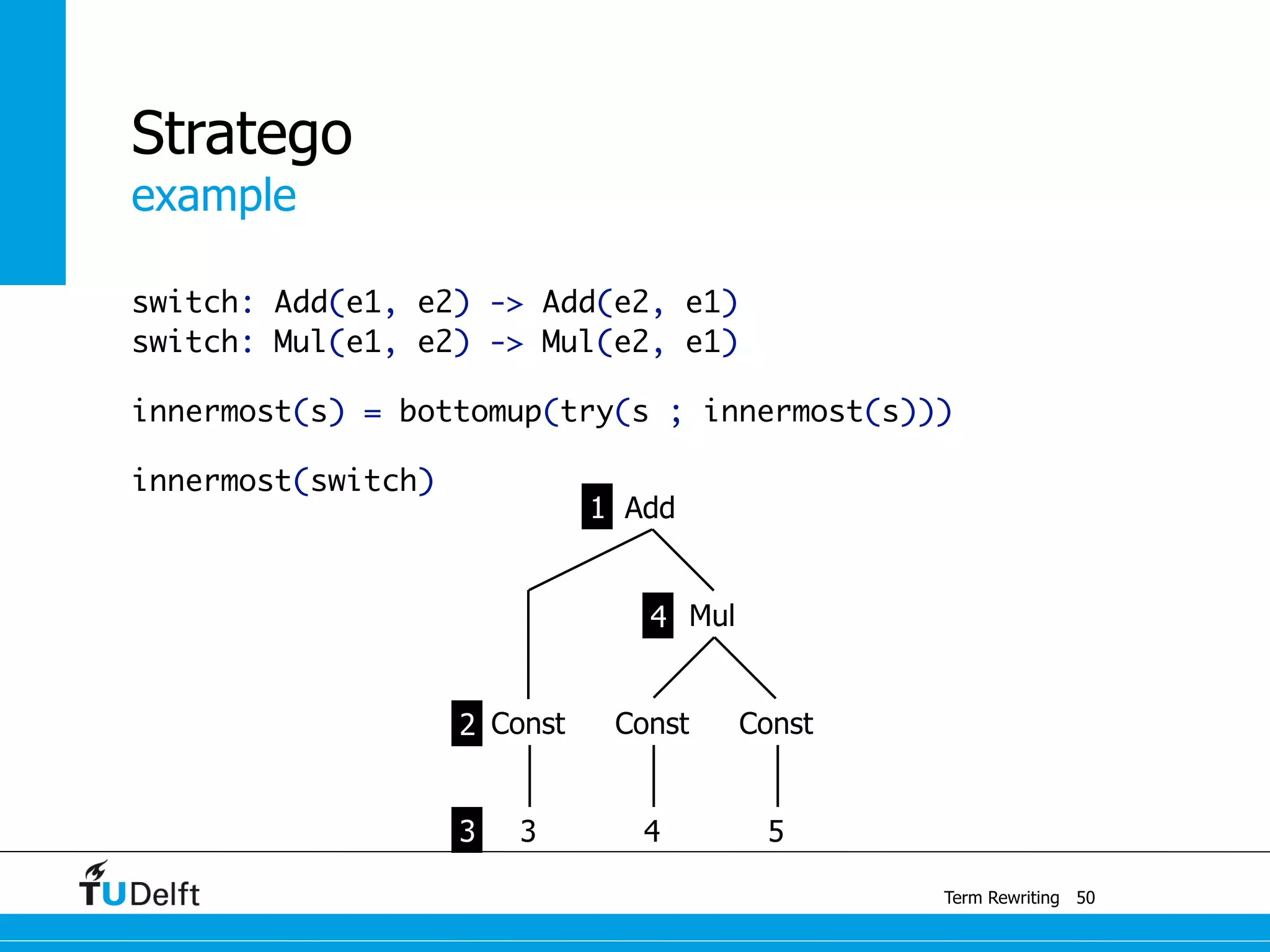
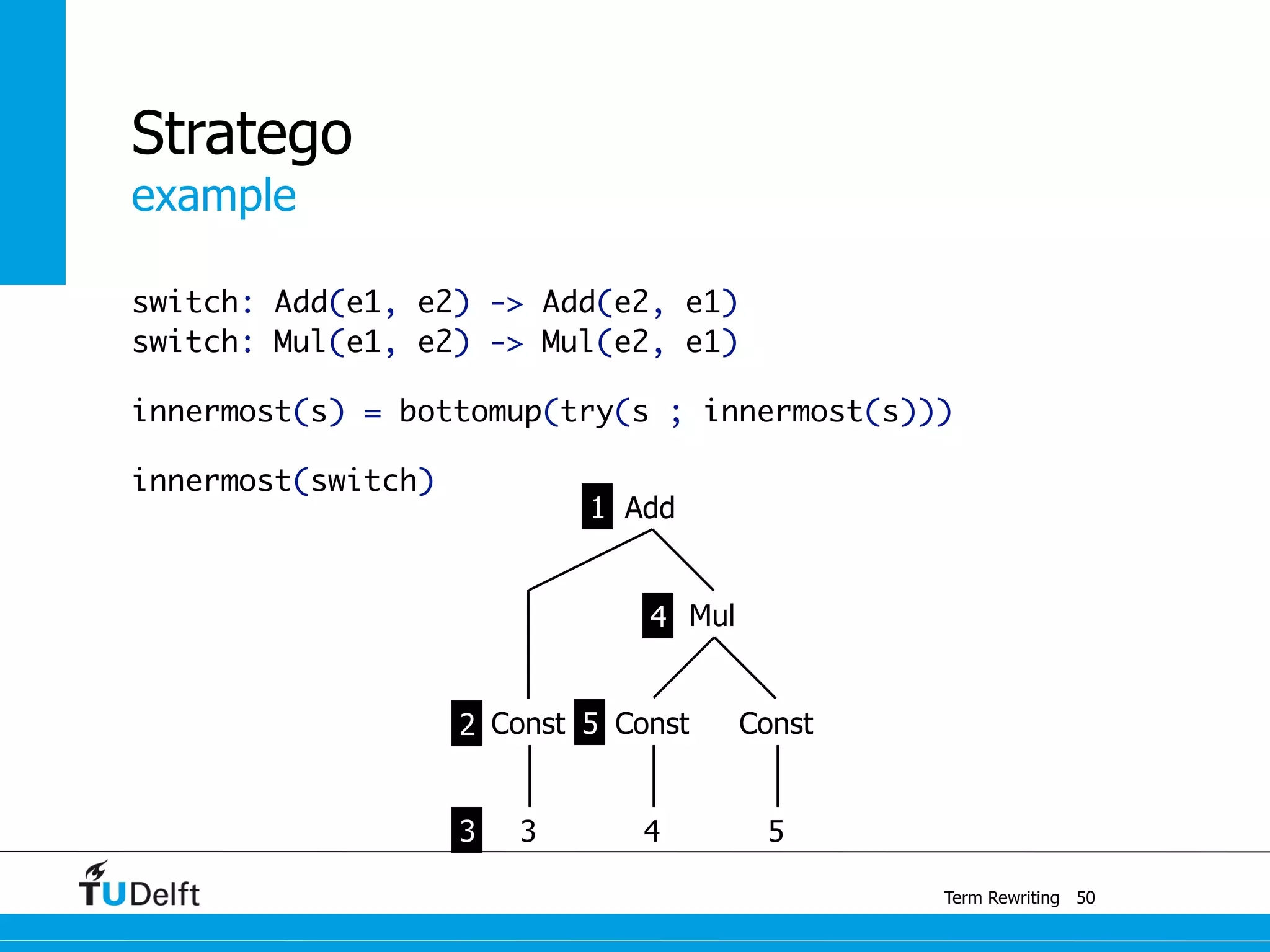
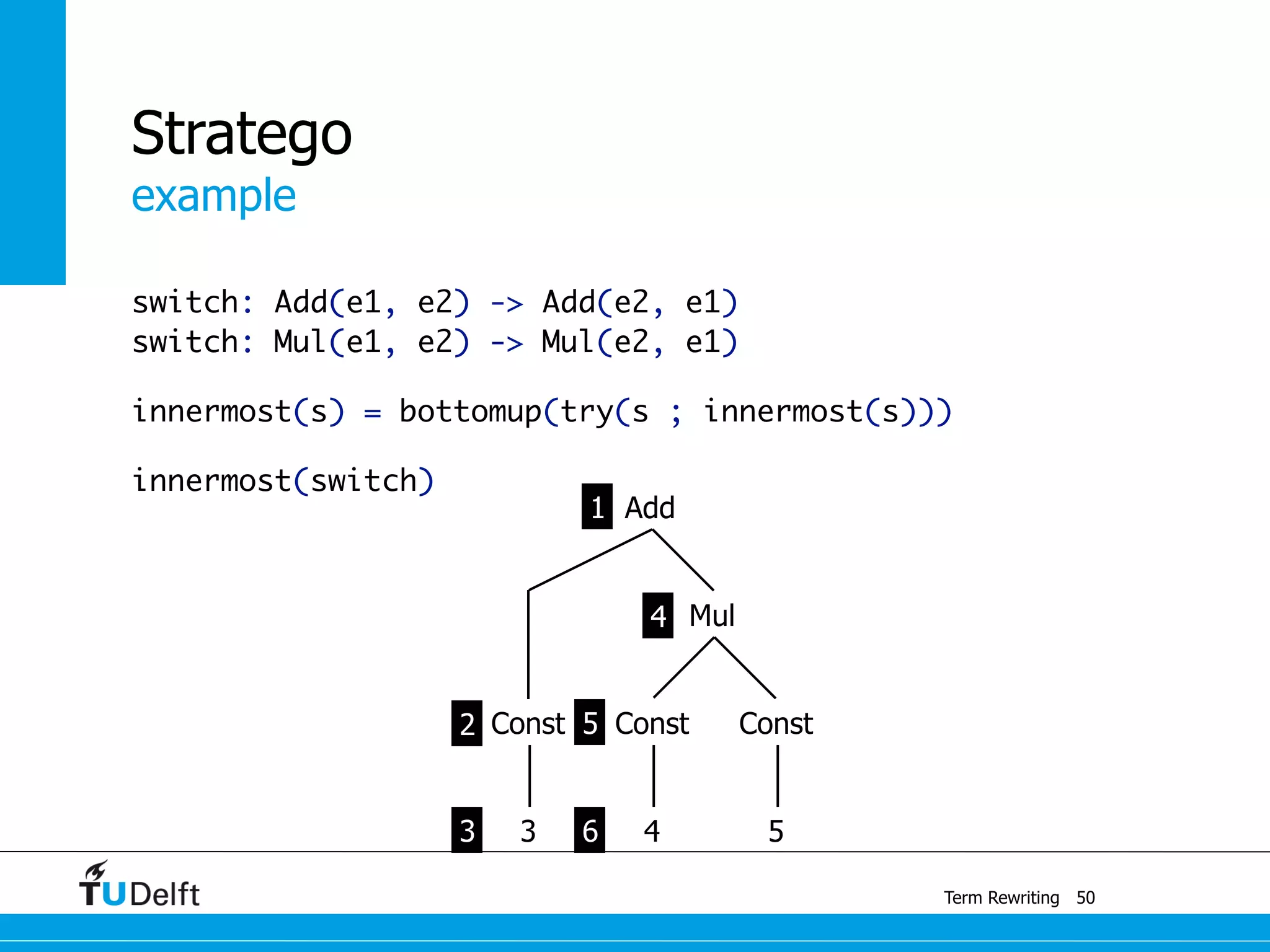
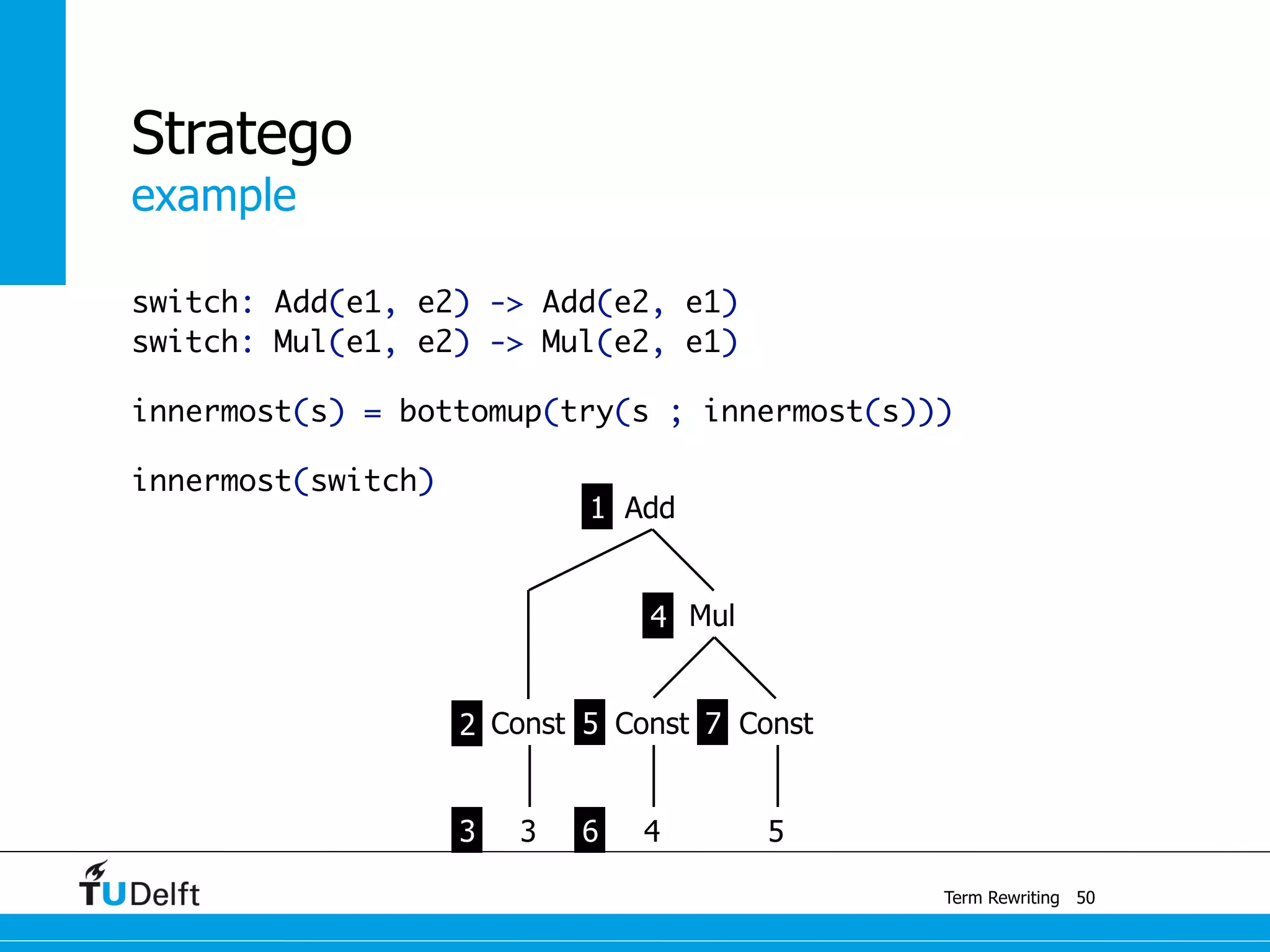
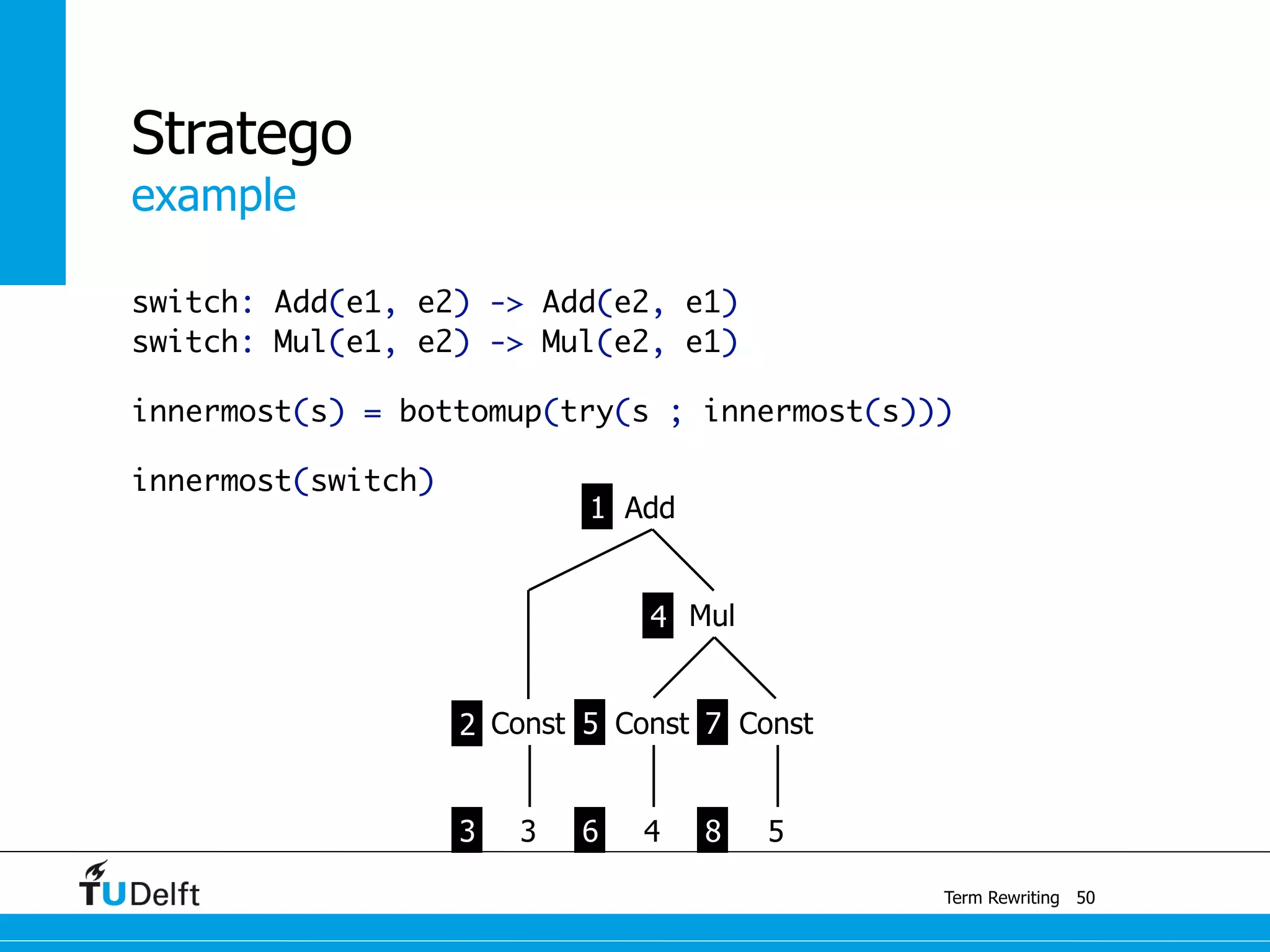
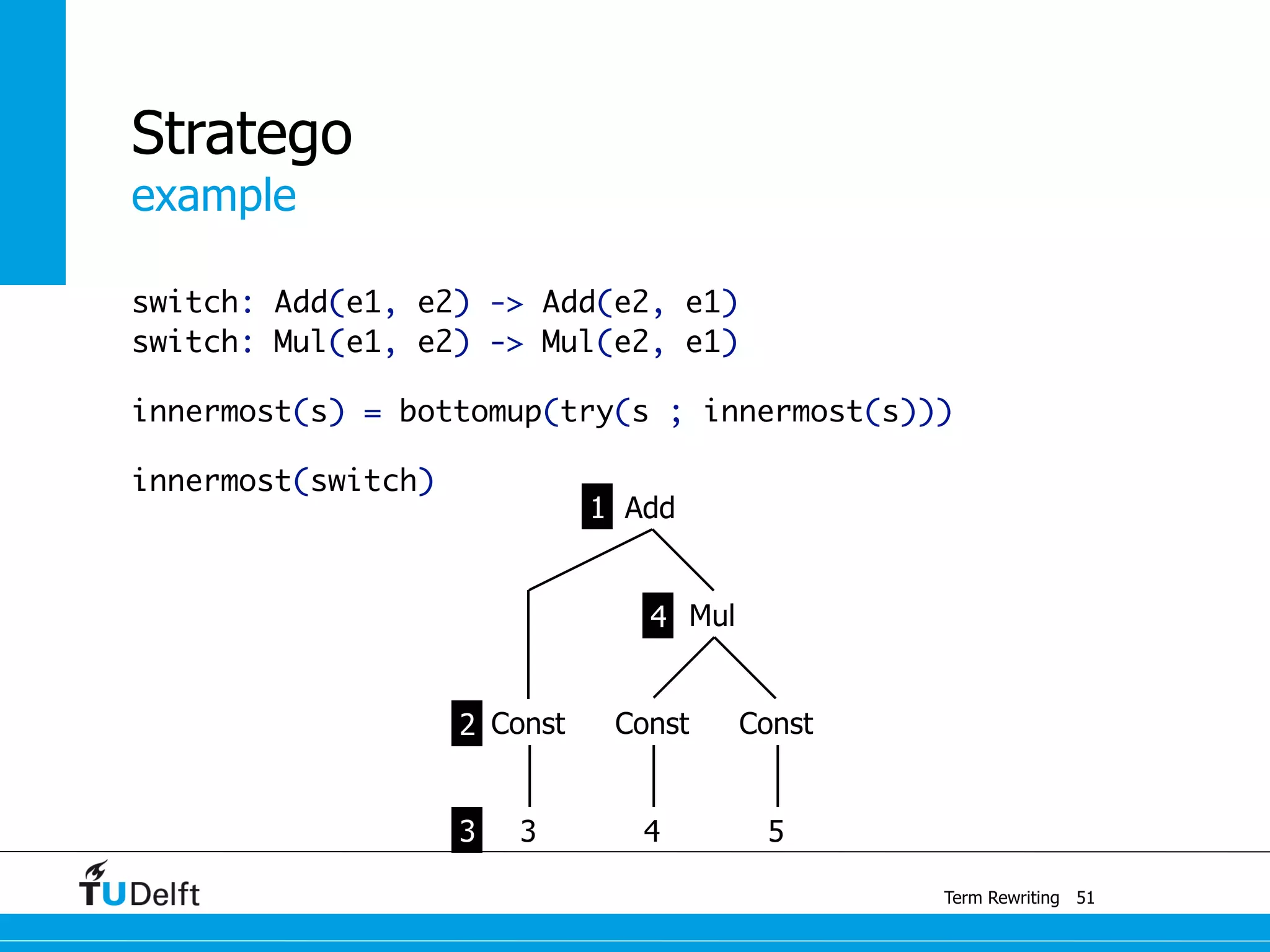
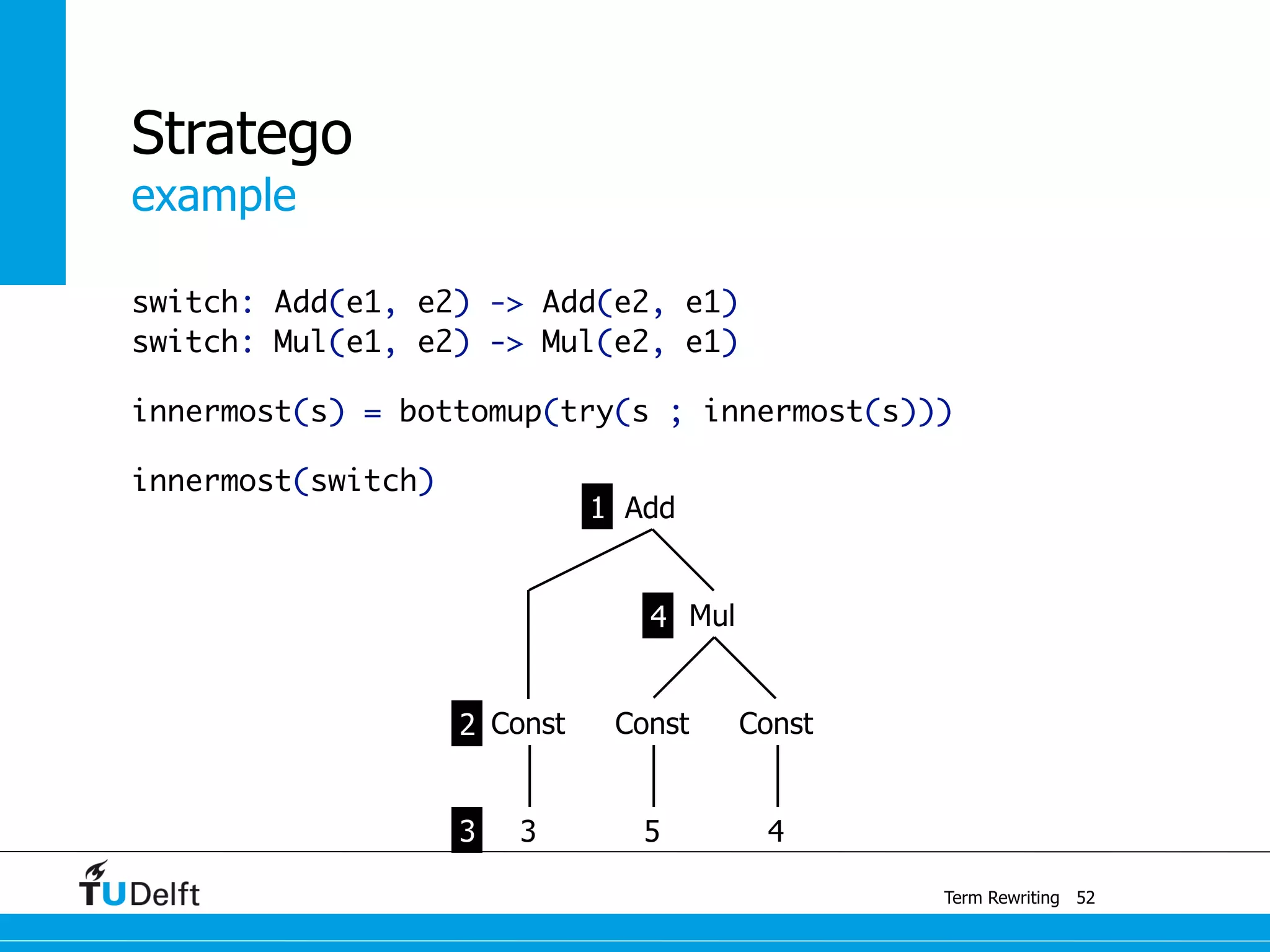
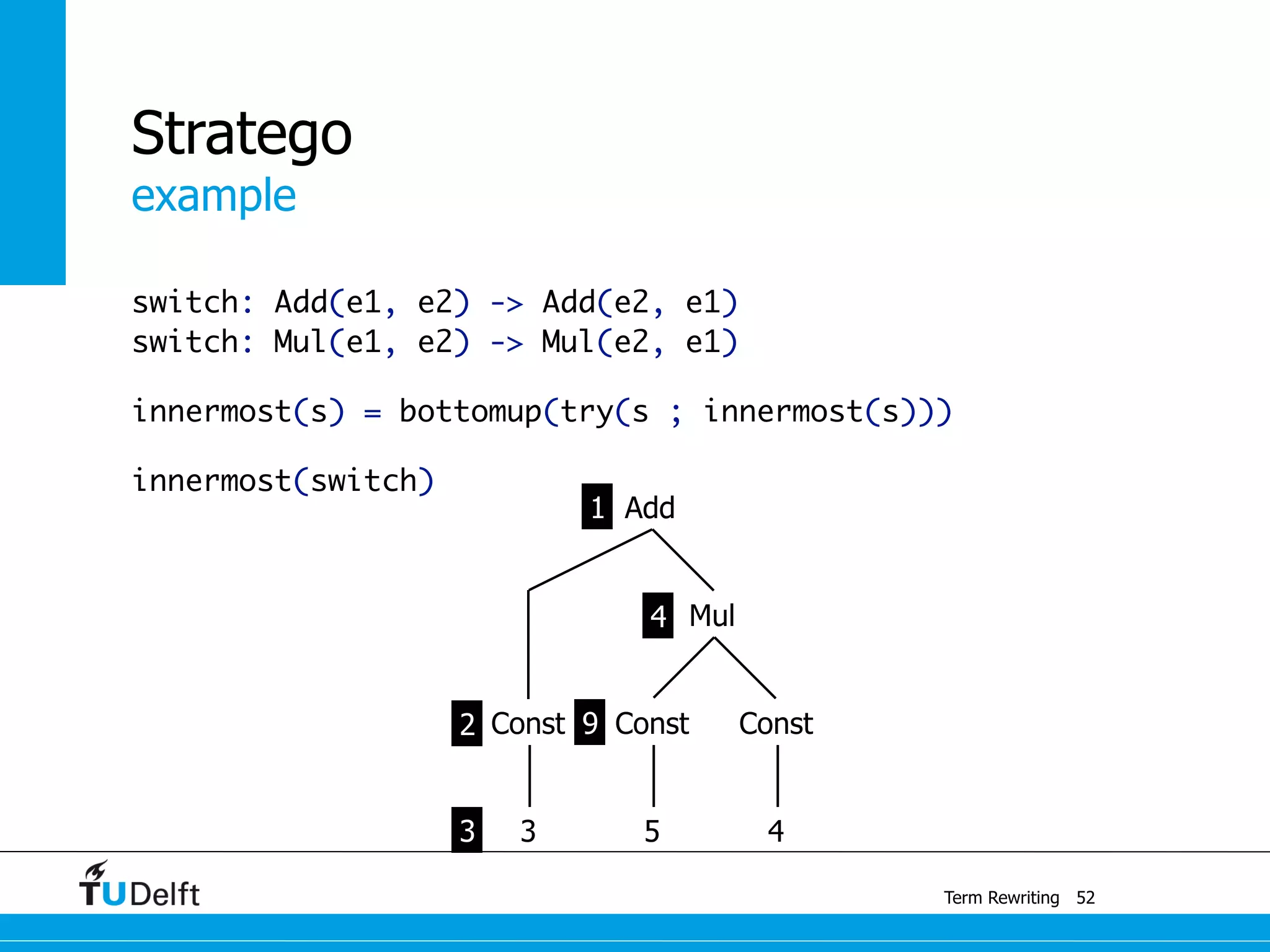
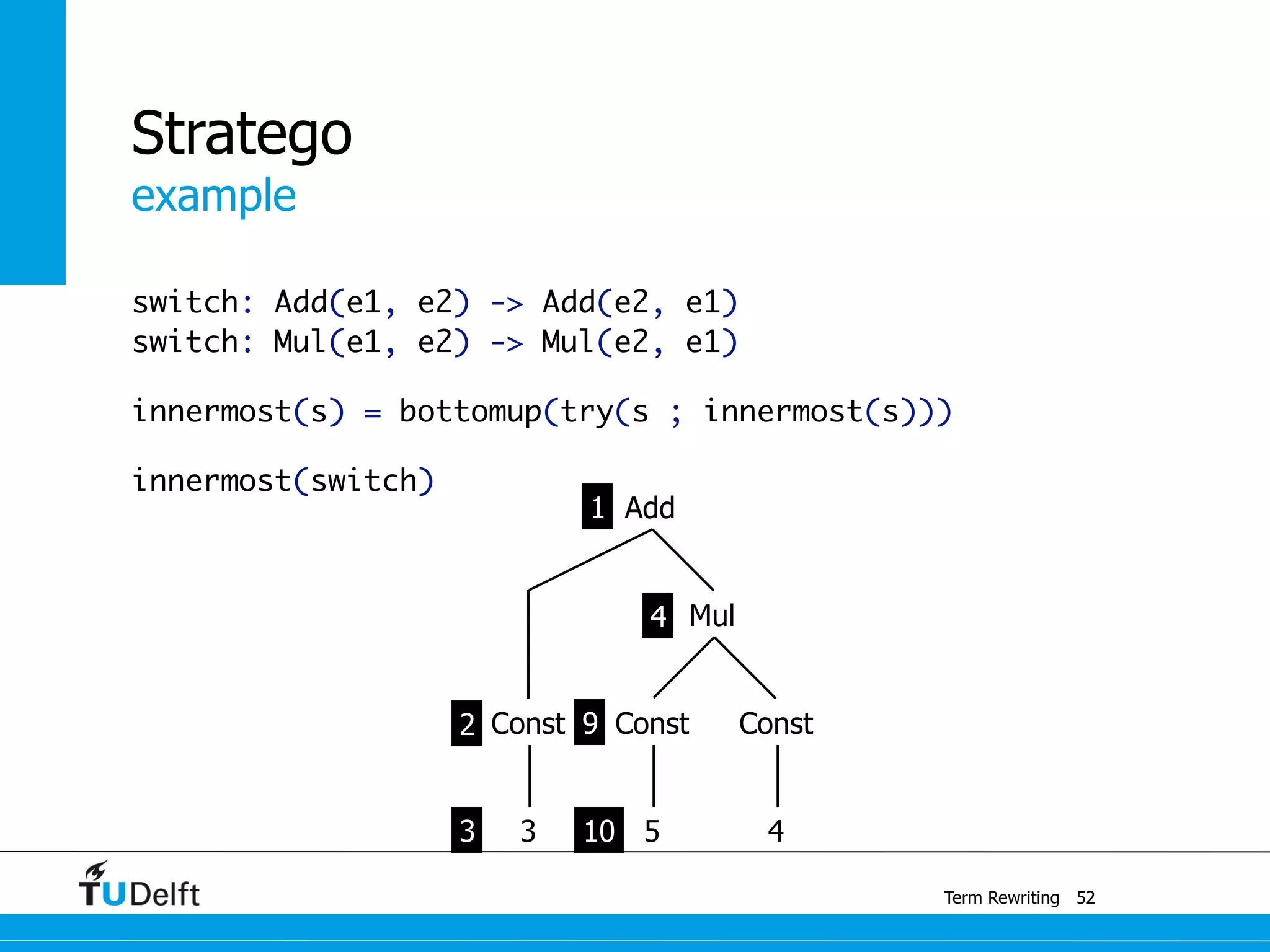
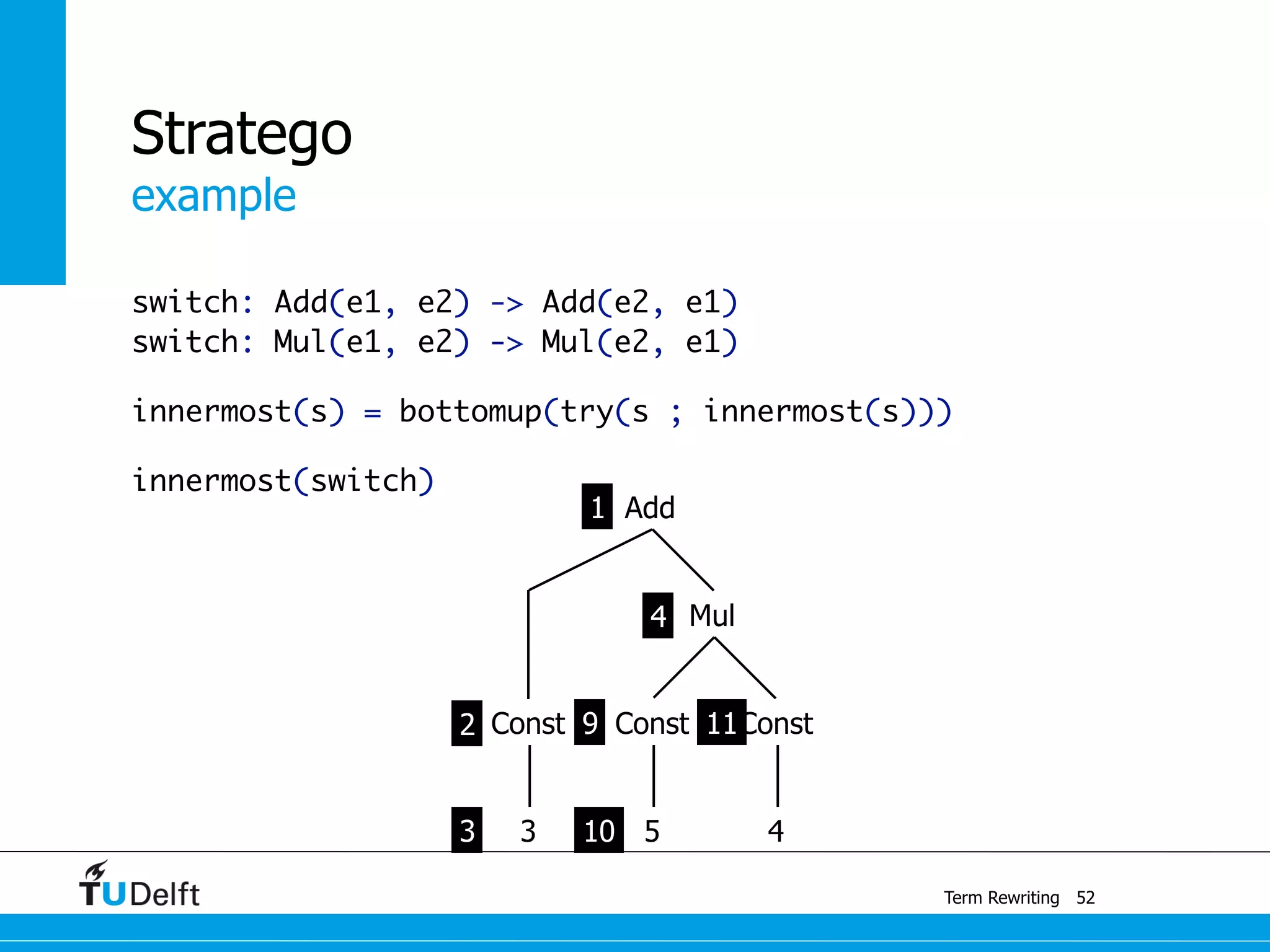
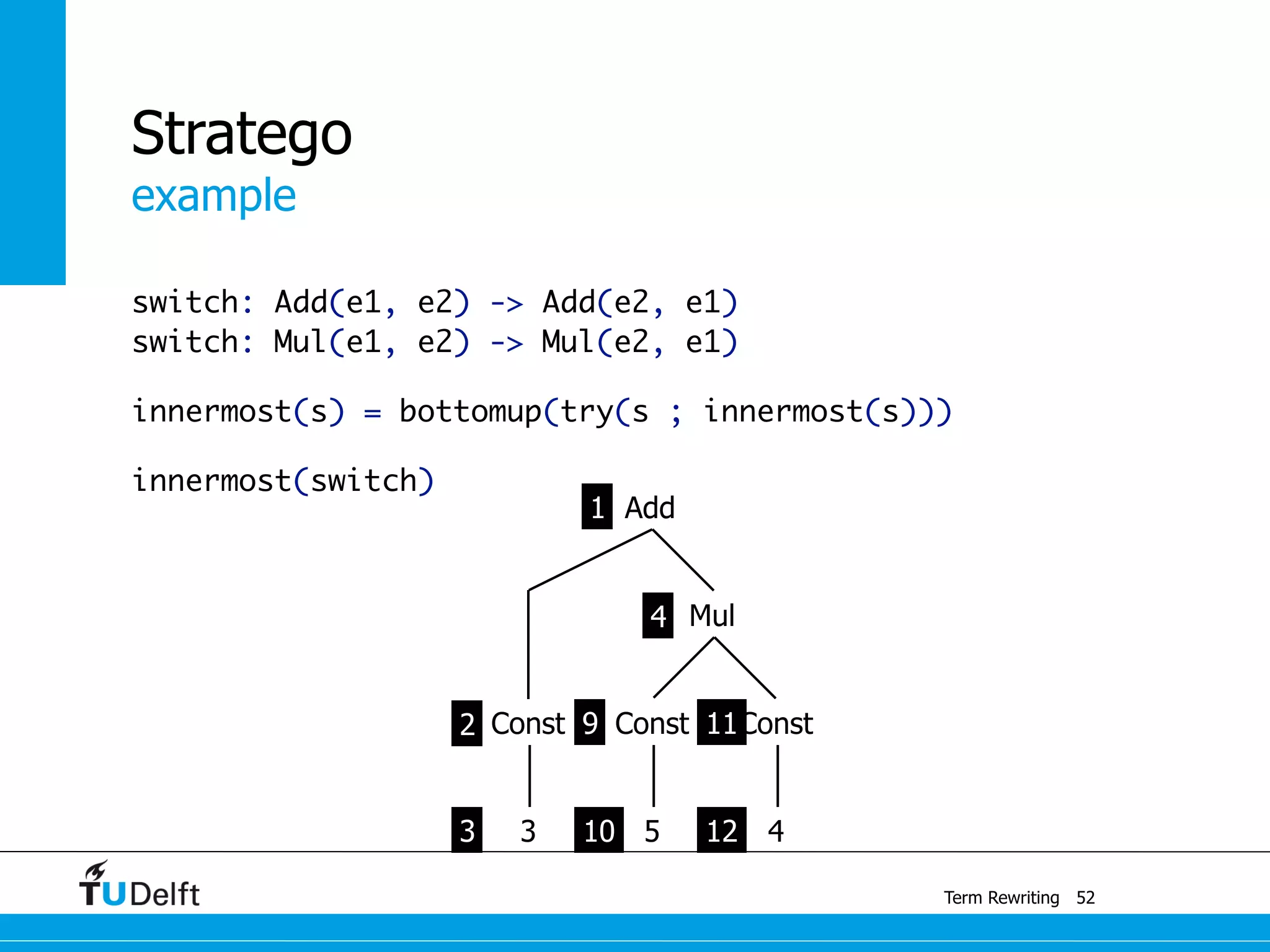
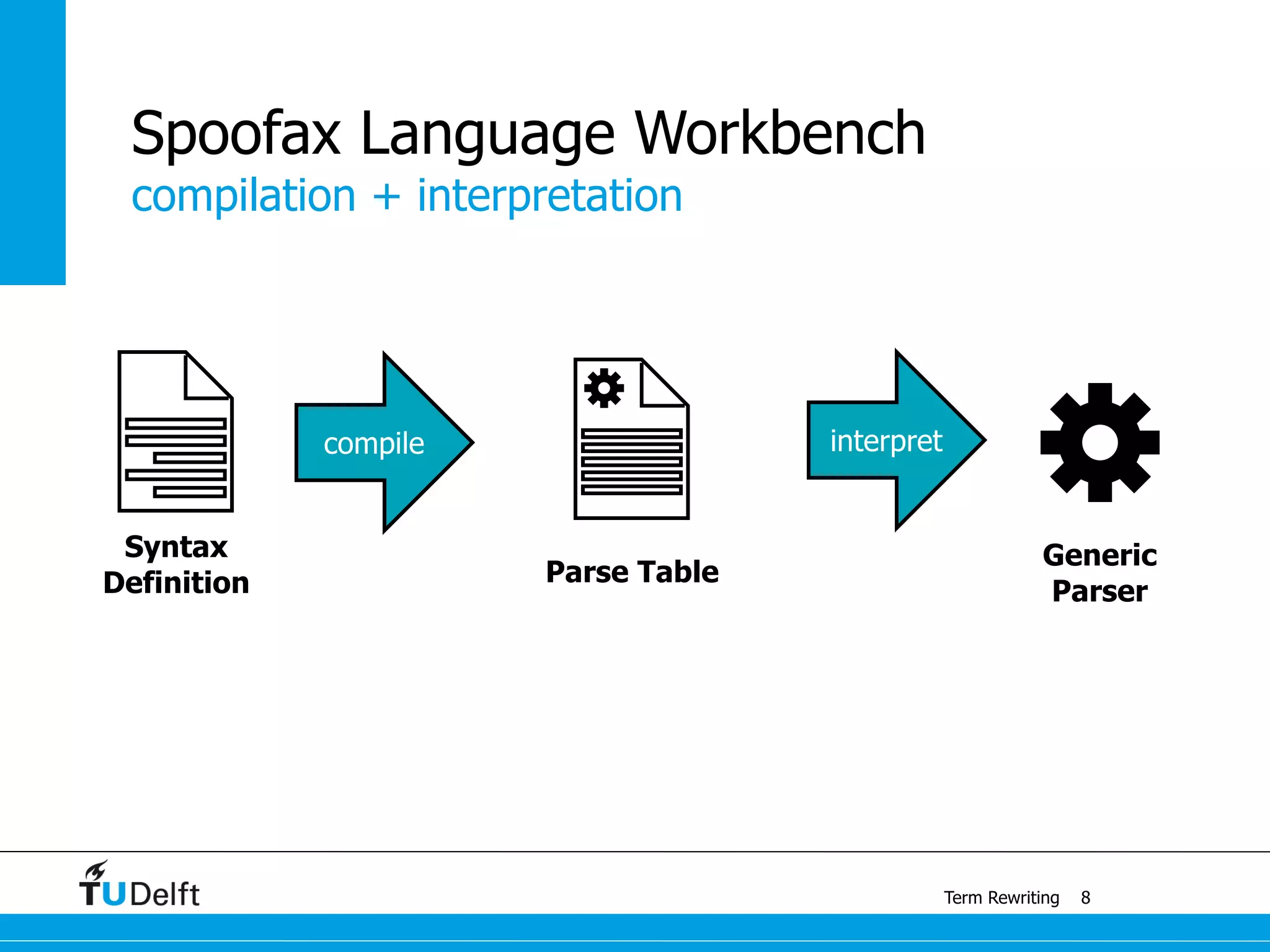
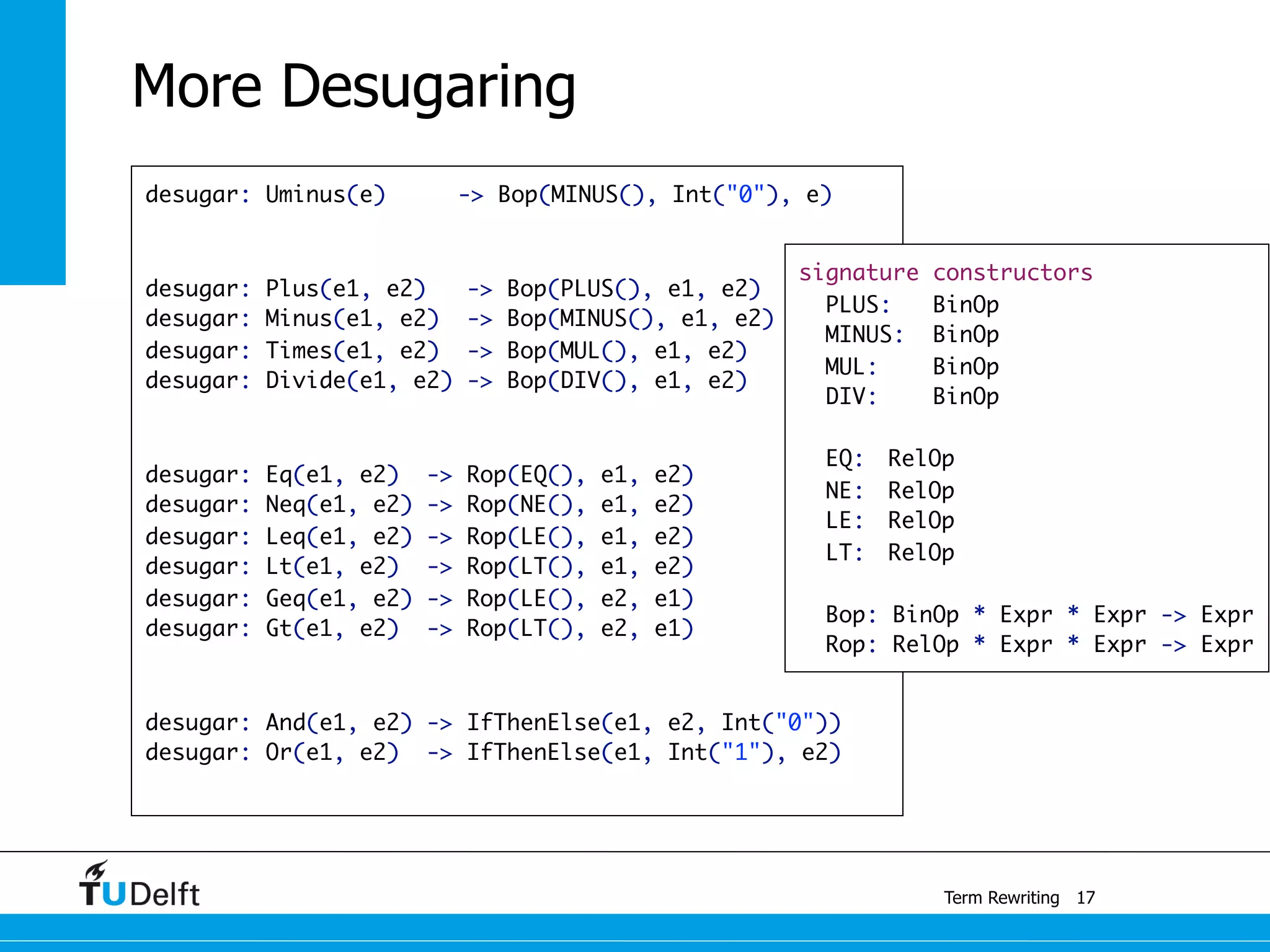
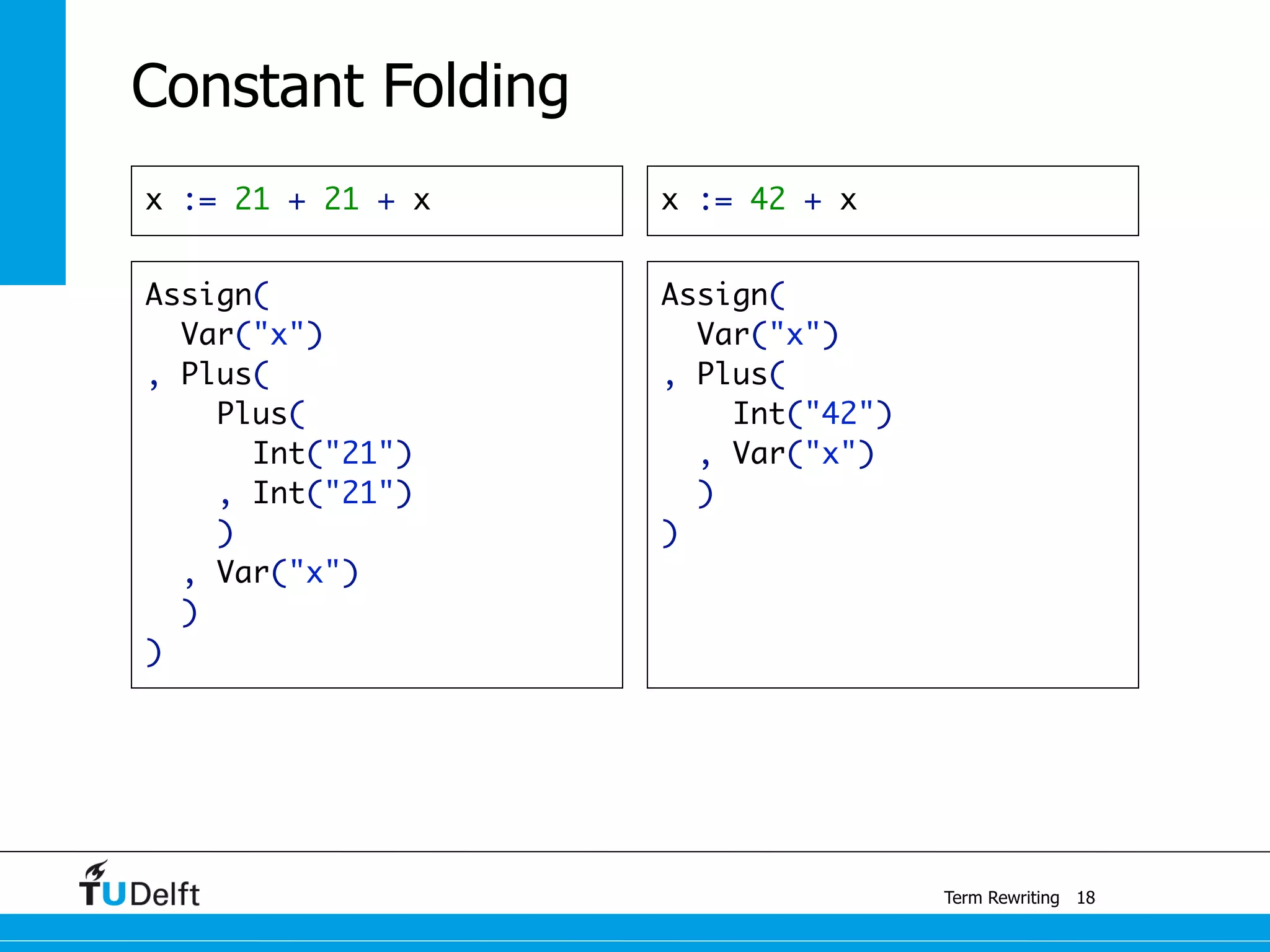
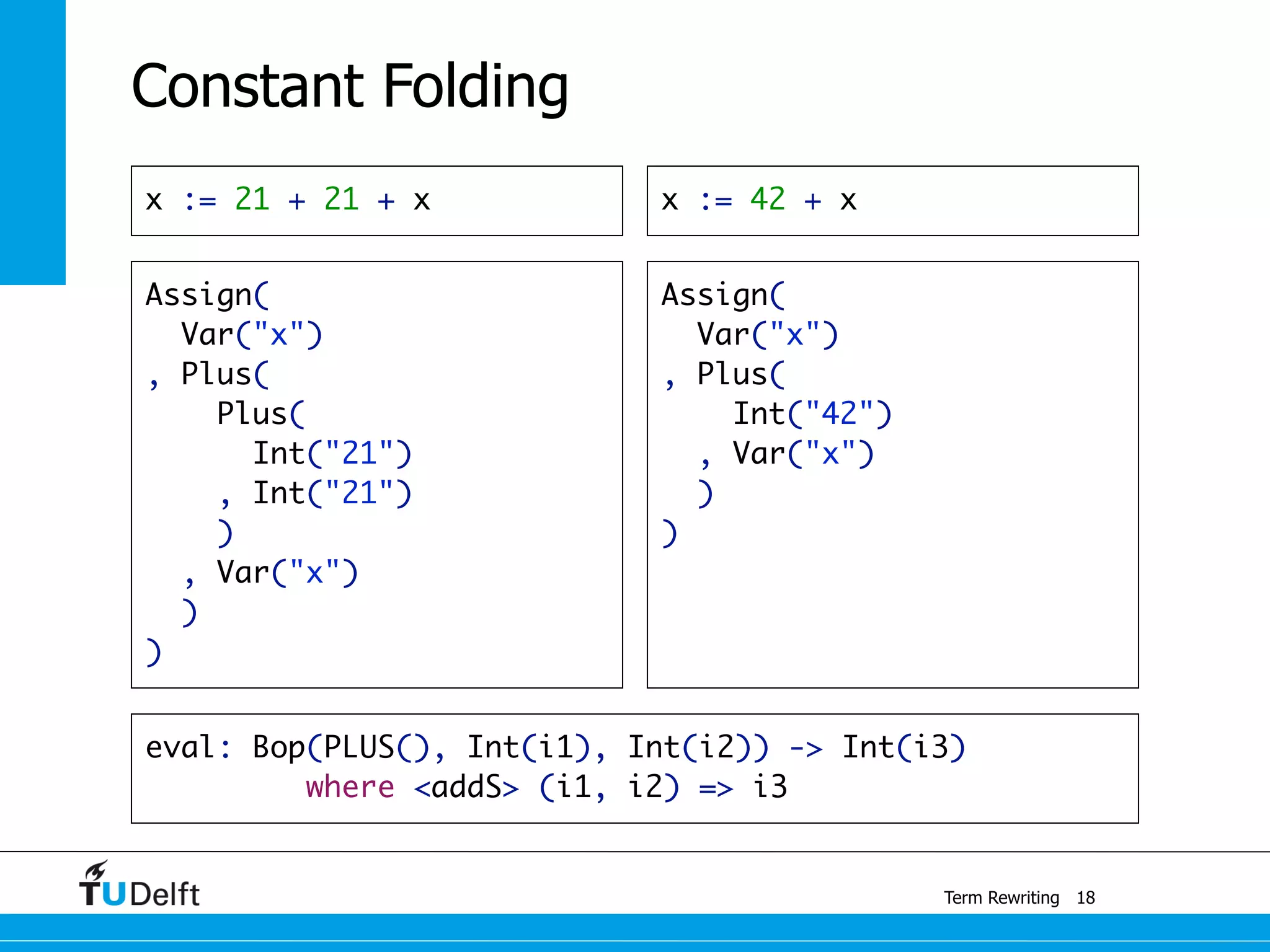
This document discusses term rewriting and its applications in compiler construction. It covers term rewriting systems, rewrite rules that transform terms, and rewrite strategies that control rule application. Examples are provided for desugaring code using rewrite rules and constant folding arithmetic expressions using rewrite rules and strategies. Stratego is presented as a domain-specific language for program transformation based on term rewriting.

Embed presentation

Download as PDF, PPTX
1 / 142
2 / 142
3 / 142
4 / 142
5 / 142
6 / 142
7 / 142
8 / 142
9 / 142
10 / 142
11 / 142
12 / 142
13 / 142
14 / 142
15 / 142
16 / 142
17 / 142
18 / 142
19 / 142
20 / 142
21 / 142
22 / 142
23 / 142
24 / 142
25 / 142
26 / 142
27 / 142
28 / 142
29 / 142
30 / 142
31 / 142
32 / 142
33 / 142
34 / 142
35 / 142
36 / 142
37 / 142
38 / 142
39 / 142
40 / 142
41 / 142
42 / 142
43 / 142
44 / 142
45 / 142
46 / 142
47 / 142
48 / 142
49 / 142
50 / 142
51 / 142
52 / 142
53 / 142
54 / 142
55 / 142
56 / 142
57 / 142
58 / 142
59 / 142
60 / 142
61 / 142
62 / 142
63 / 142
64 / 142
65 / 142
66 / 142
67 / 142
68 / 142
69 / 142
70 / 142
71 / 142
72 / 142
73 / 142
74 / 142
75 / 142
76 / 142
77 / 142
78 / 142
79 / 142
80 / 142
81 / 142
82 / 142
83 / 142
84 / 142
85 / 142
86 / 142
87 / 142
88 / 142
89 / 142
90 / 142
91 / 142
92 / 142
93 / 142
94 / 142
95 / 142
96 / 142
97 / 142
98 / 142
99 / 142
100 / 142
101 / 142
102 / 142
103 / 142
104 / 142
105 / 142
106 / 142
107 / 142
108 / 142
109 / 142
110 / 142
111 / 142
112 / 142
113 / 142
114 / 142
115 / 142
116 / 142
117 / 142
118 / 142
119 / 142
120 / 142
121 / 142
122 / 142
123 / 142
124 / 142
125 / 142
126 / 142
127 / 142
128 / 142
129 / 142
130 / 142
131 / 142
132 / 142
133 / 142
134 / 142
135 / 142
136 / 142
137 / 142
138 / 142
139 / 142
140 / 142
141 / 142
142 / 142
Challenge the future Delft University of Technology Course IN4303 2013/14 Compiler Construction Guido Wachsmuth Declarative Semantics Definition Term Rewriting
today’s lecture Term Rewriting Overview manual implementation • static analysis & error checking • code generation • semantic editor services domain-specific language • Stratego • transform ASTs • working on ATerms • declarative style 2
Term Rewriting overview I 3
architecture Term Rewriting Modern Compilers in IDEs 4 Source Code
architecture Term Rewriting Modern Compilers in IDEs 4 Source Code parse
architecture Term Rewriting Modern Compilers in IDEs 4 Source Code parse check
architecture Term Rewriting Modern Compilers in IDEs 4 Source Code parse check
architecture Term Rewriting Modern Compilers in IDEs 4 Source Code parse generate Machine Code check
manual implementation Term Rewriting Traditional Compiler Compilers 5 Language Implementation compile Compiler
compilation + compilation Term Rewriting Traditional Compiler Compilers 6 Language Implementation compile Compiler Language Definition compile
compilation + interpretation Term Rewriting Traditional Compiler Compilers 7 interpret Interpreter Language Definition compile Language Implementation
compilation + interpretation Term Rewriting Spoofax Language Workbench 8 interpret Generic Parser Syntax Definition compile Parse Table
manual implementation Term Rewriting Spoofax Language Workbench Stratego • declarative DSL • domain: program transformation • means to manipulate ASTs • working on ATerms • compiles to C or Java Stratego in Spoofax • static analysis & error checking • code generation • semantic editor services 9
concepts Term Rewriting Stratego signatures rewrite rules • transform term to term • left-hand side • pattern matching & variable binding • right-hand side • pattern instantiation & variable substitution rewrite strategies • algorithm for applying rewrite rules 10
example Term Rewriting Stratego module desugar imports include/Tiger operators strategies desugar-all = innermost(desugar) rules desugar: IfThen(e1, e2) -> IfThenElse(e1, e2, NoVal()) 11
Term Rewriting signatures II 12
context-free syntax "-" Exp -> Exp {cons("Uminus")} Exp "+" Exp -> Exp {cons("Plus")} Exp "-" Exp -> Exp {cons("Minus")} Exp "*" Exp -> Exp {cons("Times")} Exp "/" Exp -> Exp {cons("Divide")} Exp "=" Exp -> Exp {cons("Eq")} Exp "<>" Exp -> Exp {cons("Neq")} Exp ">" Exp -> Exp {cons("Gt")} Exp "<" Exp -> Exp {cons("Lt")} Exp ">=" Exp -> Exp {cons("Geq")} Exp "<=" Exp -> Exp {cons("Leq")} Exp "&" Exp -> Exp {cons("And")} Exp "|" Exp -> Exp {cons("Or")} Term Rewriting Signatures signature constructors Uminus : Exp -> Exp Plus : Exp * Exp -> Exp Minus : Exp * Exp -> Exp Times : Exp * Exp -> Exp Divide : Exp * Exp -> Exp Eq : Exp * Exp -> Exp Neq : Exp * Exp -> Exp Gt : Exp * Exp -> Exp Lt : Exp * Exp -> Exp Geq : Exp * Exp -> Exp Leq : Exp * Exp -> Exp And : Exp * Exp -> Exp Or : Exp * Exp -> Exp 13
signature Term Rewriting signature constructors Constructor : Cons -> Term Application : Cons * List(Term) -> Term List : List(Term) -> Term Tuple : List(Term) -> Term signature constructors Nil : -> List(a) Cons : a * List(a) -> List(a) Conc : List(a) * List(a) -> List(a) 14 ATerms in Stratego
Term Rewriting rewrite rules III 15
Term Rewriting Desugaring if x then printint(x) 16 if x then printint(x) else ()
Term Rewriting Desugaring if x then printint(x) 16 if x then printint(x) else () IfThen( Var("x") , Call( "printint" , [Var("x")] ) ) IfThenElse( Var("x") , Call( "printint" , [Var("x")] ) , NoVal() )
desugar: IfThen(e1, e2) -> IfThenElse(e1, e2, NoVal()) Term Rewriting Desugaring if x then printint(x) 16 if x then printint(x) else () IfThen( Var("x") , Call( "printint" , [Var("x")] ) ) IfThenElse( Var("x") , Call( "printint" , [Var("x")] ) , NoVal() )
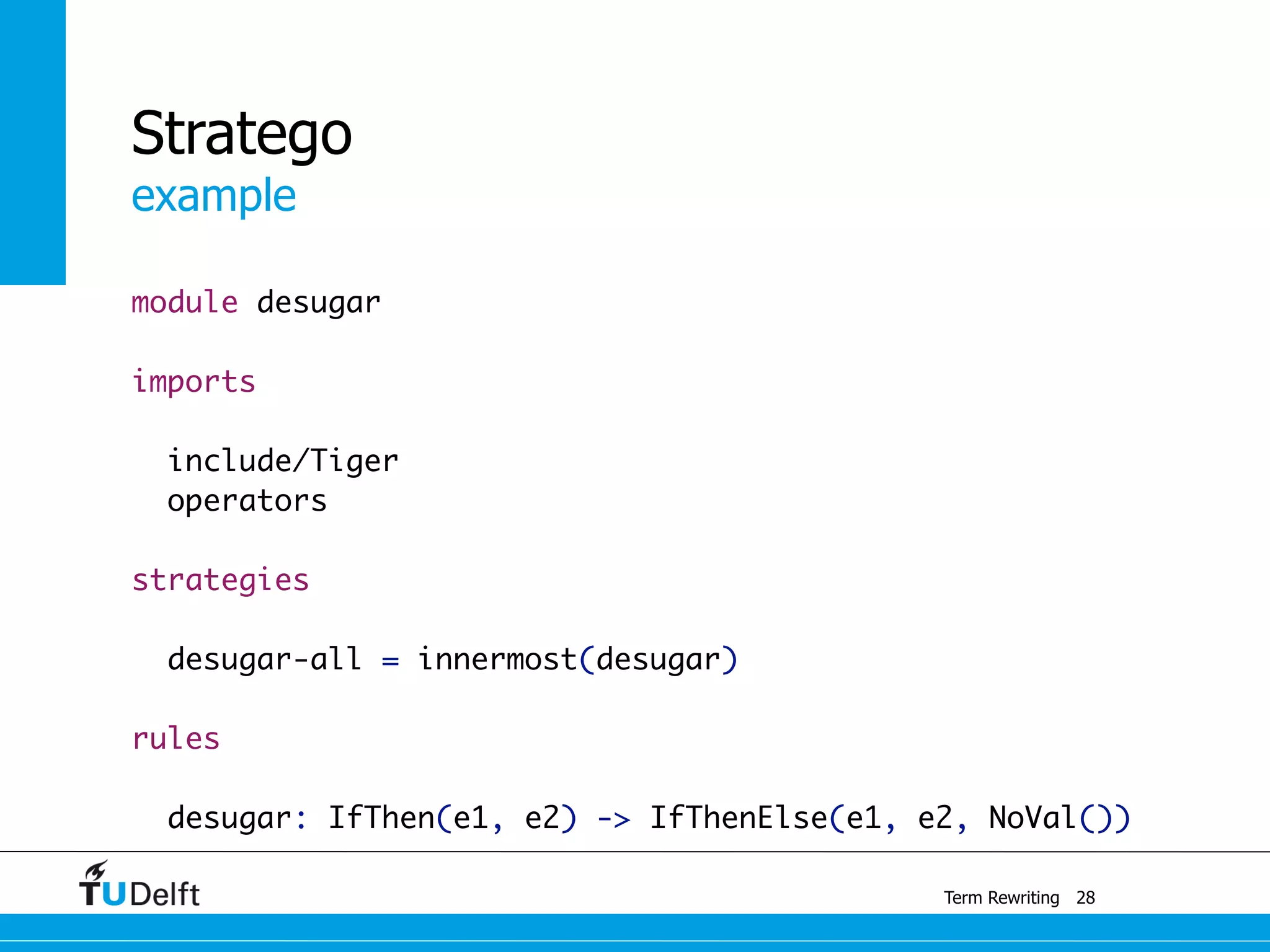
desugar: IfThen(e1, e2) -> IfThenElse(e1, e2, NoVal()) Term Rewriting Desugaring if x then printint(x) 16 if x then printint(x) else () IfThen( Var("x") , Call( "printint" , [Var("x")] ) ) IfThenElse( Var("x") , Call( "printint" , [Var("x")] ) , NoVal() ) pattern matching
desugar: IfThen(e1, e2) -> IfThenElse(e1, e2, NoVal()) Term Rewriting Desugaring if x then printint(x) 16 if x then printint(x) else () IfThen( Var("x") , Call( "printint" , [Var("x")] ) ) IfThenElse( Var("x") , Call( "printint" , [Var("x")] ) , NoVal() ) pattern matching e1 e2
desugar: IfThen(e1, e2) -> IfThenElse(e1, e2, NoVal()) Term Rewriting Desugaring if x then printint(x) 16 if x then printint(x) else () IfThen( Var("x") , Call( "printint" , [Var("x")] ) ) IfThenElse( Var("x") , Call( "printint" , [Var("x")] ) , NoVal() ) pattern matching pattern instantiation e1 e2
desugar: IfThen(e1, e2) -> IfThenElse(e1, e2, NoVal()) Term Rewriting Desugaring if x then printint(x) 16 if x then printint(x) else () IfThen( Var("x") , Call( "printint" , [Var("x")] ) ) IfThenElse( Var("x") , Call( "printint" , [Var("x")] ) , NoVal() ) pattern matching pattern instantiation e1 e2
desugar: Uminus(e) -> Bop(MINUS(), Int("0"), e) desugar: Plus(e1, e2) -> Bop(PLUS(), e1, e2) desugar: Minus(e1, e2) -> Bop(MINUS(), e1, e2) desugar: Times(e1, e2) -> Bop(MUL(), e1, e2) desugar: Divide(e1, e2) -> Bop(DIV(), e1, e2) desugar: Eq(e1, e2) -> Rop(EQ(), e1, e2) desugar: Neq(e1, e2) -> Rop(NE(), e1, e2) desugar: Leq(e1, e2) -> Rop(LE(), e1, e2) desugar: Lt(e1, e2) -> Rop(LT(), e1, e2) desugar: Geq(e1, e2) -> Rop(LE(), e2, e1) desugar: Gt(e1, e2) -> Rop(LT(), e2, e1) desugar: And(e1, e2) -> IfThenElse(e1, e2, Int("0")) desugar: Or(e1, e2) -> IfThenElse(e1, Int("1"), e2) Term Rewriting More Desugaring signature constructors PLUS: BinOp MINUS: BinOp MUL: BinOp DIV: BinOp EQ: RelOp NE: RelOp LE: RelOp LT: RelOp Bop: BinOp * Expr * Expr -> Expr Rop: RelOp * Expr * Expr -> Expr 17
Term Rewriting Constant Folding x := 21 + 21 + x 18 x := 42 + x
Term Rewriting Constant Folding x := 21 + 21 + x 18 x := 42 + x Assign( Var("x") , Plus( Plus( Int("21") , Int("21") ) , Var("x") ) ) Assign( Var("x") , Plus( Int("42") , Var("x") ) )
eval: Bop(PLUS(), Int(i1), Int(i2)) -> Int(i3) where <addS> (i1, i2) => i3 Term Rewriting Constant Folding x := 21 + 21 + x 18 x := 42 + x Assign( Var("x") , Plus( Plus( Int("21") , Int("21") ) , Var("x") ) ) Assign( Var("x") , Plus( Int("42") , Var("x") ) )
eval: Bop(PLUS(), Int(i1), Int(i2)) -> Int(<addS> (i1, i2)) eval: Bop(MINUS(), Int(i1), Int(i2)) -> Int(<subtS> (i1, i2)) eval: Bop(MUL(), Int(i1), Int(i2)) -> Int(<mulS> (i1, i2)) eval: Bop(DIV(), Int(i1), Int(i2)) -> Int(<divS> (i1, i2)) eval: Rop(EQ(), Int(i), Int(i)) -> Int("1") eval: Rop(EQ(), Int(i1), Int(i2)) -> Int("0") where not( <eq> (i1, i2) ) eval: Rop(NE(), Int(i), Int(i)) -> Int("0") eval: Rop(NE(), Int(i1), Int(i2)) -> Int("1") where not( <eq> (i1, i2) ) eval: Rop(LT(), Int(i1), Int(i2)) -> Int("1") where <ltS> (i1, i2) eval: Rop(LT(), Int(i1), Int(i2)) -> Int("0") where not( <ltS> (i1, i2) ) eval: Rop(LE(), Int(i1), Int(i2)) -> Int("1") where <leqS> (i1, i2) eval: Rop(LE(), Int(i1), Int(i2)) -> Int("0") where not( <leqS> (i1, i2)) Term Rewriting More Constant Folding 19
parameters Term Rewriting Rewrite Rules f(x,y|a,b): lhs -> rhs • strategy or rule parameters x,y • term parameters a,b • no matching f(|a,b): lhs -> rhs • optional strategy parameters f(x,y): lhs -> rhs • optional term parameters f: lhs -> rhs 20
example: map Term Rewriting Rules with Parameters 21 [ 1 , 2 , 3 ] [ 2 , 3 , 4 ] map(inc)
example: map Term Rewriting Rules with Parameters 21 [ 1 , 2 , 3 ] [ 2 , 3 , 4 ] map(inc) inc 1 2 3 2 3 4inc inc
example: map Term Rewriting Rules with Parameters map(s): [] -> [] map(s): [x|xs] -> [<s> x | <map(s)> xs] 21 [ 1 , 2 , 3 ] [ 2 , 3 , 4 ] map(inc) inc 1 2 3 2 3 4inc inc
example: zip Term Rewriting Rules with Parameters 22 [ 1 , 2 , 3 ] [ (1,4) , (2,5) , (3,6) ] [ 4 , 5 , 6 ]zip
example: zip Term Rewriting Rules with Parameters 22 [ 1 , 2 , 3 ] [ (1,4) , (2,5) , (3,6) ] [ 4 , 5 , 6 ]zip [ 1 , 2 , 3 ] [ 5 , 7 , 9 ] [ 4 , 5 , 6 ]zip(add)
example: zip Term Rewriting Rules with Parameters 22 [ 1 , 2 , 3 ] [ (1,4) , (2,5) , (3,6) ] [ 4 , 5 , 6 ]zip [ 1 , 2 , 3 ] [ 5 , 7 , 9 ] [ 4 , 5 , 6 ]zip(add) map(add)
example: zip Term Rewriting Rules with Parameters zip(s): ([],[]) -> [] zip(s): ([x|xs],[y|ys]) -> [<s> (x,y) | <zip(s)> (xs,ys)] zip = zip(id) 22 [ 1 , 2 , 3 ] [ (1,4) , (2,5) , (3,6) ] [ 4 , 5 , 6 ]zip [ 1 , 2 , 3 ] [ 5 , 7 , 9 ] [ 4 , 5 , 6 ]zip(add) map(add)
example: fold Term Rewriting Rules with Parameters 23 [1,2,3] foldr(!0,add) 6
example: fold Term Rewriting Rules with Parameters 23 [1,2,3] foldr(!0,add) 6 [] 0 [3] 3 [2,3] 56 [1,2,3]
example: fold Term Rewriting Rules with Parameters foldr(s1,s2): [] -> <s1> foldr(s1,s2): [x|xs] -> <s2> (x,<foldr(s1,s2)> xs) 23 [1,2,3] foldr(!0,add) 6 [] 0 [3] 3 [2,3] 56 [1,2,3]
example: inverse Term Rewriting Rules with Parameters 24 [1,2,3] inverse(|[]) [3,2,1]
example: inverse Term Rewriting Rules with Parameters 24 [1,2,3] inverse(|[]) [3,2,1] [2,3] [1][] [1,2,3] [3] [2,1] [3,2,1] []
example: inverse Term Rewriting Rules with Parameters inverse(|is): [] -> is inverse(|is): [x|xs] -> <inverse(|[x|is])> xs 24 [1,2,3] inverse(|[]) [3,2,1] [2,3] [1][] [1,2,3] [3] [2,1] [3,2,1] []
Term Rewriting 25 coffee break
Term Rewriting rewrite strategies IV 26
rules and strategies Term Rewriting Transformation Definitions rewrite rules • term to term • left-hand side matching • right-hand side instantiation • conditional • partial transformation rewrite strategies • rule selection • algorithm • composition of transformations 27
example Term Rewriting Stratego module desugar imports include/Tiger operators strategies desugar-all = innermost(desugar) rules desugar: IfThen(e1, e2) -> IfThenElse(e1, e2, NoVal()) 28
example Term Rewriting Stratego module eval imports include/Tiger operators desugar strategies eval-all = innermost(desugar + eval) rules eval: Bop(PLUS(),Int(i1),Int(i2)) -> Int(i3) where <addS> (i1, i2) => i3 29
Term Rewriting Strategy Combinators identity id 30
Term Rewriting Strategy Combinators identity id failure fail 30
Term Rewriting Strategy Combinators identity id failure fail sequential composition s1 ; s2 30
Term Rewriting Strategy Combinators identity id failure fail sequential composition s1 ; s2 deterministic choice s1 <+ s2 30
Term Rewriting Strategy Combinators identity id failure fail sequential composition s1 ; s2 deterministic choice s1 <+ s2 non-deterministic choice s1 + s2 30
Term Rewriting Strategy Combinators identity id failure fail sequential composition s1 ; s2 deterministic choice s1 <+ s2 non-deterministic choice s1 + s2 guarded choice s1 < s2 + s3 30
variables Term Rewriting Strategy Combinators pattern matching ?t 31
variables Term Rewriting Strategy Combinators pattern matching ?t pattern instantiation !t 31
variables Term Rewriting Strategy Combinators pattern matching ?t pattern instantiation !t strategy application <s> t ≣ !t ; s 31
variables Term Rewriting Strategy Combinators pattern matching ?t pattern instantiation !t strategy application <s> t ≣ !t ; s result matching s => t ≣ s ; ?t <s> t1 => t2 t2 := <s> t1 31
variables Term Rewriting Strategy Combinators pattern matching ?t pattern instantiation !t strategy application <s> t ≣ !t ; s result matching s => t ≣ s ; ?t <s> t1 => t2 t2 := <s> t1 variable scope {x,y: s} 31
rules and strategies Term Rewriting Strategy Combinators named rewrite rule l: t1 -> t2 where s ≣ l = ?t1 ; s ; !t2 32
rules and strategies Term Rewriting Strategy Combinators named rewrite rule l: t1 -> t2 where s ≣ l = ?t1 ; s ; !t2 unscoped rewrite rule (t1 -> t2 where s) ≣ ?t1 ; s ; !t2 32
rules and strategies Term Rewriting Strategy Combinators named rewrite rule l: t1 -> t2 where s ≣ l = ?t1 ; s ; !t2 unscoped rewrite rule (t1 -> t2 where s) ≣ ?t1 ; s ; !t2 strategy definition f(x,y|a,b) = s 32
examples Term Rewriting Strategy Combinators try(s) = s <+ id repeat(s) = try(s ; repeat(s)) 33
examples Term Rewriting Strategy Combinators try(s) = s <+ id repeat(s) = try(s ; repeat(s)) topdown(s) = s ; all(topdown(s)) 33
examples Term Rewriting Strategy Combinators try(s) = s <+ id repeat(s) = try(s ; repeat(s)) topdown(s) = s ; all(topdown(s)) alltd(s) = s <+ all(alltd(s)) 33
examples Term Rewriting Strategy Combinators try(s) = s <+ id repeat(s) = try(s ; repeat(s)) topdown(s) = s ; all(topdown(s)) alltd(s) = s <+ all(alltd(s)) bottomup(s) = all(bottomup(s)) ; s innermost(s) = bottomup(try(s ; innermost(s))) oncetd(s) = s <+ one(oncetd(s)) contains(|t) = oncetd(?t) 33
examples Term Rewriting Strategy Combinators try(s) = s <+ id repeat(s) = try(s ; repeat(s)) topdown(s) = s ; all(topdown(s)) alltd(s) = s <+ all(alltd(s)) bottomup(s) = all(bottomup(s)) ; s innermost(s) = bottomup(try(s ; innermost(s))) oncetd(s) = s <+ one(oncetd(s)) contains(|t) = oncetd(?t) 33
examples Term Rewriting Strategy Combinators try(s) = s <+ id repeat(s) = try(s ; repeat(s)) topdown(s) = s ; all(topdown(s)) alltd(s) = s <+ all(alltd(s)) bottomup(s) = all(bottomup(s)) ; s innermost(s) = bottomup(try(s ; innermost(s))) oncetd(s) = s <+ one(oncetd(s)) contains(|t) = oncetd(?t) 33
examples Term Rewriting Strategy Combinators try(s) = s <+ id repeat(s) = try(s ; repeat(s)) topdown(s) = s ; all(topdown(s)) alltd(s) = s <+ all(alltd(s)) bottomup(s) = all(bottomup(s)) ; s innermost(s) = bottomup(try(s ; innermost(s))) oncetd(s) = s <+ one(oncetd(s)) contains(|t) = oncetd(?t) 33
examples Term Rewriting Strategy Combinators try(s) = s <+ id repeat(s) = try(s ; repeat(s)) topdown(s) = s ; all(topdown(s)) alltd(s) = s <+ all(alltd(s)) bottomup(s) = all(bottomup(s)) ; s innermost(s) = bottomup(try(s ; innermost(s))) oncetd(s) = s <+ one(oncetd(s)) contains(|t) = oncetd(?t) 33
example Term Rewriting Stratego switch: Add(e1, e2) -> Add(e2, e1) switch: Mul(e1, e2) -> Mul(e2, e1) topdown(s) = s ; all(topdown(s)) topdown(switch) 34 Const Mul Const 3 4 5 Const Add
example Term Rewriting Stratego switch: Add(e1, e2) -> Add(e2, e1) switch: Mul(e1, e2) -> Mul(e2, e1) topdown(s) = s ; all(topdown(s)) topdown(switch) 34 Const Mul Const 3 4 5 Const Add1
example Term Rewriting Stratego switch: Add(e1, e2) -> Add(e2, e1) switch: Mul(e1, e2) -> Mul(e2, e1) topdown(s) = s ; all(topdown(s)) topdown(switch) 35 Mul Const 3 Const 4 5 Const Add1
example Term Rewriting Stratego switch: Add(e1, e2) -> Add(e2, e1) switch: Mul(e1, e2) -> Mul(e2, e1) topdown(s) = s ; all(topdown(s)) topdown(switch) 35 Mul Const 3 Const 4 5 Const Add1 2
example Term Rewriting Stratego switch: Add(e1, e2) -> Add(e2, e1) switch: Mul(e1, e2) -> Mul(e2, e1) topdown(s) = s ; all(topdown(s)) topdown(switch) 36 Mul Const 3 Const 5 4 Const Add1 2
example Term Rewriting Stratego switch: Add(e1, e2) -> Add(e2, e1) switch: Mul(e1, e2) -> Mul(e2, e1) topdown(s) = s ; all(topdown(s)) topdown(switch) 36 Mul Const 3 Const 5 4 Const Add1 2 3
example Term Rewriting Stratego switch: Add(e1, e2) -> Add(e2, e1) switch: Mul(e1, e2) -> Mul(e2, e1) topdown(s) = s ; all(topdown(s)) topdown(try(switch)) 37 Const Mul Const 3 4 5 Const Add
example Term Rewriting Stratego switch: Add(e1, e2) -> Add(e2, e1) switch: Mul(e1, e2) -> Mul(e2, e1) topdown(s) = s ; all(topdown(s)) topdown(try(switch)) 37 Const Mul Const 3 4 5 Const Add1
example Term Rewriting Stratego switch: Add(e1, e2) -> Add(e2, e1) switch: Mul(e1, e2) -> Mul(e2, e1) topdown(s) = s ; all(topdown(s)) topdown(try(switch)) 38 Mul Const 3 Const 4 5 Const Add1
example Term Rewriting Stratego switch: Add(e1, e2) -> Add(e2, e1) switch: Mul(e1, e2) -> Mul(e2, e1) topdown(s) = s ; all(topdown(s)) topdown(try(switch)) 38 Mul Const 3 Const 4 5 Const Add1 2
example Term Rewriting Stratego switch: Add(e1, e2) -> Add(e2, e1) switch: Mul(e1, e2) -> Mul(e2, e1) topdown(s) = s ; all(topdown(s)) topdown(try(switch)) 39 Mul Const 3 Const 5 4 Const Add1 2
example Term Rewriting Stratego switch: Add(e1, e2) -> Add(e2, e1) switch: Mul(e1, e2) -> Mul(e2, e1) topdown(s) = s ; all(topdown(s)) topdown(try(switch)) 39 Mul Const 3 Const 5 4 Const Add1 2 3
example Term Rewriting Stratego switch: Add(e1, e2) -> Add(e2, e1) switch: Mul(e1, e2) -> Mul(e2, e1) topdown(s) = s ; all(topdown(s)) topdown(try(switch)) 39 Mul Const 3 Const 5 4 Const Add1 2 3 4
example Term Rewriting Stratego switch: Add(e1, e2) -> Add(e2, e1) switch: Mul(e1, e2) -> Mul(e2, e1) topdown(s) = s ; all(topdown(s)) topdown(try(switch)) 39 Mul Const 3 Const 5 4 Const Add1 2 3 4 5
example Term Rewriting Stratego switch: Add(e1, e2) -> Add(e2, e1) switch: Mul(e1, e2) -> Mul(e2, e1) topdown(s) = s ; all(topdown(s)) topdown(try(switch)) 39 Mul Const 3 Const 5 4 Const Add1 2 3 4 5 6
example Term Rewriting Stratego switch: Add(e1, e2) -> Add(e2, e1) switch: Mul(e1, e2) -> Mul(e2, e1) topdown(s) = s ; all(topdown(s)) topdown(try(switch)) 39 Mul Const 3 Const 5 4 Const Add1 2 3 4 5 6 7
example Term Rewriting Stratego switch: Add(e1, e2) -> Add(e2, e1) switch: Mul(e1, e2) -> Mul(e2, e1) topdown(s) = s ; all(topdown(s)) topdown(try(switch)) 39 Mul Const 3 Const 5 4 Const Add1 2 3 4 5 6 7 8
example Term Rewriting Stratego switch: Add(e1, e2) -> Add(e2, e1) switch: Mul(e1, e2) -> Mul(e2, e1) alltd(s) = s <+ all(alltd(s)) alltd(switch) 40 Const Mul Const 3 4 5 Const Add
example Term Rewriting Stratego switch: Add(e1, e2) -> Add(e2, e1) switch: Mul(e1, e2) -> Mul(e2, e1) alltd(s) = s <+ all(alltd(s)) alltd(switch) 40 Const Mul Const 3 4 5 Const Add1
example Term Rewriting Stratego switch: Add(e1, e2) -> Add(e2, e1) switch: Mul(e1, e2) -> Mul(e2, e1) alltd(s) = s <+ all(alltd(s)) alltd(switch) 41 Mul Const 3 Const 4 5 Const Add1
example Term Rewriting Stratego switch: Mul(e1, e2) -> Mul(e2, e1) alltd(s) = s <+ all(alltd(s)) alltd(switch) 42 Const Mul Const 3 4 5 Const Add
example Term Rewriting Stratego switch: Mul(e1, e2) -> Mul(e2, e1) alltd(s) = s <+ all(alltd(s)) alltd(switch) 42 Const Mul Const 3 4 5 Const Add1
example Term Rewriting Stratego switch: Mul(e1, e2) -> Mul(e2, e1) alltd(s) = s <+ all(alltd(s)) alltd(switch) 42 Const Mul Const 3 4 5 Const Add1 2
example Term Rewriting Stratego switch: Mul(e1, e2) -> Mul(e2, e1) alltd(s) = s <+ all(alltd(s)) alltd(switch) 42 Const Mul Const 3 4 5 Const Add1 2 3
example Term Rewriting Stratego switch: Mul(e1, e2) -> Mul(e2, e1) alltd(s) = s <+ all(alltd(s)) alltd(switch) 42 Const Mul Const 3 4 5 Const Add1 2 3 4
example Term Rewriting Stratego switch: Mul(e1, e2) -> Mul(e2, e1) alltd(s) = s <+ all(alltd(s)) alltd(switch) 43 Const Mul Const 3 5 4 Const Add1 2 3 4
example Term Rewriting Stratego switch: Add(e1, e2) -> Add(e2, e1) switch: Mul(e1, e2) -> Mul(e2, e1) bottomup(s) = all(bottomup(s)) ; s bottomup(switch) 44 Const Mul Const 3 4 5 Const Add
example Term Rewriting Stratego switch: Add(e1, e2) -> Add(e2, e1) switch: Mul(e1, e2) -> Mul(e2, e1) bottomup(s) = all(bottomup(s)) ; s bottomup(switch) 44 Const Mul Const 3 4 5 Const Add1
example Term Rewriting Stratego switch: Add(e1, e2) -> Add(e2, e1) switch: Mul(e1, e2) -> Mul(e2, e1) bottomup(s) = all(bottomup(s)) ; s bottomup(switch) 44 Const Mul Const 3 4 5 Const Add1 2
example Term Rewriting Stratego switch: Add(e1, e2) -> Add(e2, e1) switch: Mul(e1, e2) -> Mul(e2, e1) bottomup(s) = all(bottomup(s)) ; s bottomup(switch) 44 Const Mul Const 3 4 5 Const Add1 2 3
example Term Rewriting Stratego switch: Add(e1, e2) -> Add(e2, e1) switch: Mul(e1, e2) -> Mul(e2, e1) bottomup(s) = all(bottomup(s)) ; s bottomup(try(switch)) 45 Const Mul Const 3 4 5 Const Add
example Term Rewriting Stratego switch: Add(e1, e2) -> Add(e2, e1) switch: Mul(e1, e2) -> Mul(e2, e1) bottomup(s) = all(bottomup(s)) ; s bottomup(try(switch)) 45 Const Mul Const 3 4 5 Const Add1
example Term Rewriting Stratego switch: Add(e1, e2) -> Add(e2, e1) switch: Mul(e1, e2) -> Mul(e2, e1) bottomup(s) = all(bottomup(s)) ; s bottomup(try(switch)) 45 Const Mul Const 3 4 5 Const Add1 2
example Term Rewriting Stratego switch: Add(e1, e2) -> Add(e2, e1) switch: Mul(e1, e2) -> Mul(e2, e1) bottomup(s) = all(bottomup(s)) ; s bottomup(try(switch)) 45 Const Mul Const 3 4 5 Const Add1 2 3
example Term Rewriting Stratego switch: Add(e1, e2) -> Add(e2, e1) switch: Mul(e1, e2) -> Mul(e2, e1) bottomup(s) = all(bottomup(s)) ; s bottomup(try(switch)) 45 Const Mul Const 3 4 5 Const Add1 2 3 4
example Term Rewriting Stratego switch: Add(e1, e2) -> Add(e2, e1) switch: Mul(e1, e2) -> Mul(e2, e1) bottomup(s) = all(bottomup(s)) ; s bottomup(try(switch)) 45 Const Mul Const 3 4 5 Const Add1 2 3 4 5
example Term Rewriting Stratego switch: Add(e1, e2) -> Add(e2, e1) switch: Mul(e1, e2) -> Mul(e2, e1) bottomup(s) = all(bottomup(s)) ; s bottomup(try(switch)) 45 Const Mul Const 3 4 5 Const Add1 2 3 4 5 6
example Term Rewriting Stratego switch: Add(e1, e2) -> Add(e2, e1) switch: Mul(e1, e2) -> Mul(e2, e1) bottomup(s) = all(bottomup(s)) ; s bottomup(try(switch)) 45 Const Mul Const 3 4 5 Const Add1 2 3 4 5 6 7
example Term Rewriting Stratego switch: Add(e1, e2) -> Add(e2, e1) switch: Mul(e1, e2) -> Mul(e2, e1) bottomup(s) = all(bottomup(s)) ; s bottomup(try(switch)) 45 Const Mul Const 3 4 5 Const Add1 2 3 4 5 6 7 8
example Term Rewriting Stratego switch: Add(e1, e2) -> Add(e2, e1) switch: Mul(e1, e2) -> Mul(e2, e1) bottomup(s) = all(bottomup(s)) ; s bottomup(try(switch)) 46 Const Mul Const 3 4 5 Const Add1 2 3 4
example Term Rewriting Stratego switch: Add(e1, e2) -> Add(e2, e1) switch: Mul(e1, e2) -> Mul(e2, e1) bottomup(s) = all(bottomup(s)) ; s bottomup(try(switch)) 47 Const Mul Const 3 5 4 Const Add1 2 3 4
example Term Rewriting Stratego switch: Add(e1, e2) -> Add(e2, e1) switch: Mul(e1, e2) -> Mul(e2, e1) bottomup(s) = all(bottomup(s)) ; s bottomup(try(switch)) 48 Const Mul Const 3 5 4 Const Add1
Mul Const 3 Const 5 4 Const Add example Term Rewriting Stratego switch: Add(e1, e2) -> Add(e2, e1) switch: Mul(e1, e2) -> Mul(e2, e1) bottomup(s) = all(bottomup(s)) ; s bottomup(try(switch)) 49 1
example Term Rewriting Stratego switch: Add(e1, e2) -> Add(e2, e1) switch: Mul(e1, e2) -> Mul(e2, e1) innermost(s) = bottomup(try(s ; innermost(s))) innermost(switch) 50 Const Mul Const 3 4 5 Const Add
example Term Rewriting Stratego switch: Add(e1, e2) -> Add(e2, e1) switch: Mul(e1, e2) -> Mul(e2, e1) innermost(s) = bottomup(try(s ; innermost(s))) innermost(switch) 50 Const Mul Const 3 4 5 Const Add1
example Term Rewriting Stratego switch: Add(e1, e2) -> Add(e2, e1) switch: Mul(e1, e2) -> Mul(e2, e1) innermost(s) = bottomup(try(s ; innermost(s))) innermost(switch) 50 Const Mul Const 3 4 5 Const Add1 2
example Term Rewriting Stratego switch: Add(e1, e2) -> Add(e2, e1) switch: Mul(e1, e2) -> Mul(e2, e1) innermost(s) = bottomup(try(s ; innermost(s))) innermost(switch) 50 Const Mul Const 3 4 5 Const Add1 2 3
example Term Rewriting Stratego switch: Add(e1, e2) -> Add(e2, e1) switch: Mul(e1, e2) -> Mul(e2, e1) innermost(s) = bottomup(try(s ; innermost(s))) innermost(switch) 50 Const Mul Const 3 4 5 Const Add1 2 3 4
example Term Rewriting Stratego switch: Add(e1, e2) -> Add(e2, e1) switch: Mul(e1, e2) -> Mul(e2, e1) innermost(s) = bottomup(try(s ; innermost(s))) innermost(switch) 50 Const Mul Const 3 4 5 Const Add1 2 3 4 5
example Term Rewriting Stratego switch: Add(e1, e2) -> Add(e2, e1) switch: Mul(e1, e2) -> Mul(e2, e1) innermost(s) = bottomup(try(s ; innermost(s))) innermost(switch) 50 Const Mul Const 3 4 5 Const Add1 2 3 4 5 6
example Term Rewriting Stratego switch: Add(e1, e2) -> Add(e2, e1) switch: Mul(e1, e2) -> Mul(e2, e1) innermost(s) = bottomup(try(s ; innermost(s))) innermost(switch) 50 Const Mul Const 3 4 5 Const Add1 2 3 4 5 6 7
example Term Rewriting Stratego switch: Add(e1, e2) -> Add(e2, e1) switch: Mul(e1, e2) -> Mul(e2, e1) innermost(s) = bottomup(try(s ; innermost(s))) innermost(switch) 50 Const Mul Const 3 4 5 Const Add1 2 3 4 5 6 7 8
example Term Rewriting Stratego switch: Add(e1, e2) -> Add(e2, e1) switch: Mul(e1, e2) -> Mul(e2, e1) innermost(s) = bottomup(try(s ; innermost(s))) innermost(switch) 51 Const Mul Const 3 4 5 Const Add1 2 3 4
example Term Rewriting Stratego switch: Add(e1, e2) -> Add(e2, e1) switch: Mul(e1, e2) -> Mul(e2, e1) innermost(s) = bottomup(try(s ; innermost(s))) innermost(switch) 52 Const Mul Const 3 5 4 Const Add1 2 3 4
example Term Rewriting Stratego switch: Add(e1, e2) -> Add(e2, e1) switch: Mul(e1, e2) -> Mul(e2, e1) innermost(s) = bottomup(try(s ; innermost(s))) innermost(switch) 52 Const Mul Const 3 5 4 Const Add1 2 3 4 9
example Term Rewriting Stratego switch: Add(e1, e2) -> Add(e2, e1) switch: Mul(e1, e2) -> Mul(e2, e1) innermost(s) = bottomup(try(s ; innermost(s))) innermost(switch) 52 Const Mul Const 3 5 4 Const Add1 2 3 4 9 10
example Term Rewriting Stratego switch: Add(e1, e2) -> Add(e2, e1) switch: Mul(e1, e2) -> Mul(e2, e1) innermost(s) = bottomup(try(s ; innermost(s))) innermost(switch) 52 Const Mul Const 3 5 4 Const Add1 2 3 4 9 10 11
example Term Rewriting Stratego switch: Add(e1, e2) -> Add(e2, e1) switch: Mul(e1, e2) -> Mul(e2, e1) innermost(s) = bottomup(try(s ; innermost(s))) innermost(switch) 52 Const Mul Const 3 5 4 Const Add1 2 3 4 9 10 11 12
example Term Rewriting Stratego switch: Add(e1, e2) -> Add(e2, e1) switch: Mul(e1, e2) -> Mul(e2, e1) innermost(s) = bottomup(try(s ; innermost(s))) innermost(switch) 53 Const Mul Const 3 5 4 Const Add1 2 3 4
example Term Rewriting Stratego switch: Add(e1, e2) -> Add(e2, e1) switch: Mul(e1, e2) -> Mul(e2, e1) innermost(s) = bottomup(try(s ; innermost(s))) innermost(switch) 54 Const Mul Const 3 4 5 Const Add1 2 3 4
Term Rewriting summary V 55
lessons learned Term Rewriting Summary 56
lessons learned Term Rewriting Summary How do you define AST transformations in Stratego? • signatures • rewrite rules • rewrite strategies • strategy combinators 56
lessons learned Term Rewriting Summary How do you define AST transformations in Stratego? • signatures • rewrite rules • rewrite strategies • strategy combinators What kind of strategies can you find in the Stratego library? • arithmetics • map, zip, foldr • generic traversals 56
learn more Term Rewriting Literature 57
learn more Term Rewriting Literature Spoofax Lennart C. L. Kats, Eelco Visser: The Spoofax Language Workbench. Rules for Declarative Specification of Languages and IDEs. OOPSLA 2010 http://www.spoofax.org 57
learn more Term Rewriting Literature Spoofax Lennart C. L. Kats, Eelco Visser: The Spoofax Language Workbench. Rules for Declarative Specification of Languages and IDEs. OOPSLA 2010 http://www.spoofax.org Stratego Martin Bravenboer, Karl Trygve Kalleberg, Rob Vermaas, Eelco Visser: Stratego/XT 0.17. A language and toolset for program transformation. Science of Computer Programming, 72(1-2), 2008. http://www.strategoxt.org 57
coming next Term Rewriting Outlook declarative semantics definition • Lecture 5: Static Analysis and Error Checking • Lecture 6: Code Generation Assignment Oct 2: MiniJava grammar in SDF • submit on Blackboard Lab Oct 03 • syntactic editor services • pretty-printer for MiniJava 58
Term Rewriting 59
attribution & copyrights Term Rewriting Pictures Slides 1, 9, 10, 20, 27: Stratego by Kendrick Arnett, some rights reserved Slides 23-26, 28, 31, 37-39, 41-43: PICOL icons by Melih Bilgil, some rights reserved Slide 14: Thesaurus by Enoch Lau, some rights reserved Slide 21: Google Maps Street View Camera by Ian Britton, some rights reserved Slide 22: Zipper by Rabensteiner, some rights reserved Slide 23: Fold by Kim Piper Werker, some rights reserved Slide 24: Inverse by lanchongzi, some rights reserved Slide 25: Maxwell's by Dominica Williamson, some rights reserved Slide 58: Reichstag by Wolfgang Staudt, some rights reserved 60

More Related Content

PDF
Term Rewriting
byEelco Visser
 
PDF
Introduction - Imperative and Object-Oriented Languages
byGuido Wachsmuth
 
PDF
Declarative Semantics Definition - Static Analysis and Error Checking
byGuido Wachsmuth
 
PDF
Static Analysis
byEelco Visser
 
PDF
Pure and Declarative Syntax Definition: Paradise Lost and Regained
byGuido Wachsmuth
 
PDF
Static name resolution
byEelco Visser
 
PDF
Declarative Syntax Definition - Grammars and Trees
byGuido Wachsmuth
 
PDF
Lexical Analysis
byEelco Visser
 
Term Rewriting
byEelco Visser
 
Introduction - Imperative and Object-Oriented Languages
byGuido Wachsmuth
 
Declarative Semantics Definition - Static Analysis and Error Checking
byGuido Wachsmuth
 
Static Analysis
byEelco Visser
 
Pure and Declarative Syntax Definition: Paradise Lost and Regained
byGuido Wachsmuth
 
Static name resolution
byEelco Visser
 
Declarative Syntax Definition - Grammars and Trees
byGuido Wachsmuth
 
Lexical Analysis
byEelco Visser
 

What's hot

PDF
Syntax Definition
byGuido Wachsmuth
 
PDF
Dynamic Semantics
byEelco Visser
 
PDF
Syntax Definition
byEelco Visser
 
PDF
Formal Grammars
byEelco Visser
 
PDF
Declare Your Language: Syntactic (Editor) Services
byEelco Visser
 
PDF
LL Parsing
byEelco Visser
 
PDF
Compiler Components and their Generators - Traditional Parsing Algorithms
byGuido Wachsmuth
 
PDF
Declare Your Language: Syntax Definition
byEelco Visser
 
KEY
Compiler Components and their Generators - Lexical Analysis
byGuido Wachsmuth
 
PDF
Declare Your Language: Type Checking
byEelco Visser
 
PDF
Declare Your Language: Transformation by Strategic Term Rewriting
byEelco Visser
 
PDF
Declare Your Language: Name Resolution
byEelco Visser
 
PDF
Compiler Construction | Lecture 8 | Type Constraints
byEelco Visser
 
PDF
Compiler Construction | Lecture 5 | Transformation by Term Rewriting
byEelco Visser
 
PDF
CS4200 2019 | Lecture 5 | Transformation by Term Rewriting
byEelco Visser
 
PDF
Programming languages
byEelco Visser
 
PDF
Compiler Construction | Lecture 9 | Constraint Resolution
byEelco Visser
 
PDF
Dynamic Semantics Specification and Interpreter Generation
byEelco Visser
 
PDF
Ch04
byHankyo
 
PDF
Declarative Type System Specification with Statix
byEelco Visser
 
Syntax Definition
byGuido Wachsmuth
 
Dynamic Semantics
byEelco Visser
 
Syntax Definition
byEelco Visser
 
Formal Grammars
byEelco Visser
 
Declare Your Language: Syntactic (Editor) Services
byEelco Visser
 
LL Parsing
byEelco Visser
 
Compiler Components and their Generators - Traditional Parsing Algorithms
byGuido Wachsmuth
 
Declare Your Language: Syntax Definition
byEelco Visser
 
Compiler Components and their Generators - Lexical Analysis
byGuido Wachsmuth
 
Declare Your Language: Type Checking
byEelco Visser
 
Declare Your Language: Transformation by Strategic Term Rewriting
byEelco Visser
 
Declare Your Language: Name Resolution
byEelco Visser
 
Compiler Construction | Lecture 8 | Type Constraints
byEelco Visser
 
Compiler Construction | Lecture 5 | Transformation by Term Rewriting
byEelco Visser
 
CS4200 2019 | Lecture 5 | Transformation by Term Rewriting
byEelco Visser
 
Programming languages
byEelco Visser
 
Compiler Construction | Lecture 9 | Constraint Resolution
byEelco Visser
 
Dynamic Semantics Specification and Interpreter Generation
byEelco Visser
 
Ch04
byHankyo
 
Declarative Type System Specification with Statix
byEelco Visser
 

Viewers also liked

PDF
Declarative Semantics Definition - Code Generation
byGuido Wachsmuth
 
KEY
Declarative Syntax Definition - Pretty Printing
byGuido Wachsmuth
 
KEY
Compiling Imperative and Object-Oriented Languages - Activation Records
byGuido Wachsmuth
 
KEY
Compiling Imperative and Object-Oriented Languages - Dataflow Analysis
byGuido Wachsmuth
 
PDF
Domain-Specific Type Systems
byGuido Wachsmuth
 
KEY
Compiling Imperative and Object-Oriented Languages - Register Allocation
byGuido Wachsmuth
 
PDF
K to 12 TLE Curriculum Guide for Automotive
byDr. Joy Kenneth Sala Biasong
 
PDF
Compiler Components and their Generators - LR Parsing
byGuido Wachsmuth
 
KEY
Compiling Imperative and Object-Oriented Languages - Garbage Collection
byGuido Wachsmuth
 
PDF
Language
byGuido Wachsmuth
 
PPT
Definition Of Terms
byPatrice Aguillo
 
PDF
K to 12 automotive teachers guide
byNoel Tan
 
PDF
K to 12 Automotive Learning Module
byDr. Joy Kenneth Sala Biasong
 
PPTX
Beginners' Guide to Powerpoint
byLaura Hampton
 
PPSX
Research or Proposal Writing - DEFINITION OF TERMS
byJaime Alfredo Cabrera
 
PDF
K to 12 TLE Curriculum Guide
byDr. Joy Kenneth Sala Biasong
 
Declarative Semantics Definition - Code Generation
byGuido Wachsmuth
 
Declarative Syntax Definition - Pretty Printing
byGuido Wachsmuth
 
Compiling Imperative and Object-Oriented Languages - Activation Records
byGuido Wachsmuth
 
Compiling Imperative and Object-Oriented Languages - Dataflow Analysis
byGuido Wachsmuth
 
Domain-Specific Type Systems
byGuido Wachsmuth
 
Compiling Imperative and Object-Oriented Languages - Register Allocation
byGuido Wachsmuth
 
K to 12 TLE Curriculum Guide for Automotive
byDr. Joy Kenneth Sala Biasong
 
Compiler Components and their Generators - LR Parsing
byGuido Wachsmuth
 
Compiling Imperative and Object-Oriented Languages - Garbage Collection
byGuido Wachsmuth
 
Language
byGuido Wachsmuth
 
Definition Of Terms
byPatrice Aguillo
 
K to 12 automotive teachers guide
byNoel Tan
 
K to 12 Automotive Learning Module
byDr. Joy Kenneth Sala Biasong
 
Beginners' Guide to Powerpoint
byLaura Hampton
 
Research or Proposal Writing - DEFINITION OF TERMS
byJaime Alfredo Cabrera
 
K to 12 TLE Curriculum Guide
byDr. Joy Kenneth Sala Biasong
 

Similar to Declarative Semantics Definition - Term Rewriting

KEY
Verification with LoLA: 2 The LoLA Input Language
byUniversität Rostock
 
PDF
Decaf language specification
bySami Said
 
PDF
Compiler Construction | Lecture 14 | Interpreters
byEelco Visser
 
PDF
Declare Your Language: Dynamic Semantics
byEelco Visser
 
PPTX
Detecting Bugs in Binaries Using Decompilation and Data Flow Analysis
bySilvio Cesare
 
PDF
Towards a General Approach for Symbolic Model-Checker Prototyping
byEdmundo López Bóbeda
 
PDF
iRODS Rule Language Cheat Sheet
bySamuel Lampa
 
PPTX
20100522 software verification_sharygina_lecture02
byComputer Science Club
 
PDF
Micro Blaze C Reference
byiuui
 
PDF
programacion funcional.pdf
byFranciscoJavierAcost31
 
KEY
An Introduction to Functional Programming using Haskell
byMichel Rijnders
 
PDF
Rexx summary
bySylvie Migneault
 
PDF
Ff to-fp
byAndy Petrella
 
PPTX
TRICK
byJimmy Ngu
 
PPT
Compiler-Design-Intermediate-code-generation.ppt
byfargovagra
 
PPT
458237.-Compiler-Design-Intermediate-code-generation.ppt
byPalaniSamyB3
 
PDF
Slides13.pdf
byssuser3b4934
 
DOC
PCD ?s(MCA)
byguestf07b62f
 
DOC
Pcd(Mca)
byguestf07b62f
 
DOC
Pcd(Mca)
byguestf07b62f
 
Verification with LoLA: 2 The LoLA Input Language
byUniversität Rostock
 
Decaf language specification
bySami Said
 
Compiler Construction | Lecture 14 | Interpreters
byEelco Visser
 
Declare Your Language: Dynamic Semantics
byEelco Visser
 
Detecting Bugs in Binaries Using Decompilation and Data Flow Analysis
bySilvio Cesare
 
Towards a General Approach for Symbolic Model-Checker Prototyping
byEdmundo López Bóbeda
 
iRODS Rule Language Cheat Sheet
bySamuel Lampa
 
20100522 software verification_sharygina_lecture02
byComputer Science Club
 
Micro Blaze C Reference
byiuui
 
programacion funcional.pdf
byFranciscoJavierAcost31
 
An Introduction to Functional Programming using Haskell
byMichel Rijnders
 
Rexx summary
bySylvie Migneault
 
Ff to-fp
byAndy Petrella
 
TRICK
byJimmy Ngu
 
Compiler-Design-Intermediate-code-generation.ppt
byfargovagra
 
458237.-Compiler-Design-Intermediate-code-generation.ppt
byPalaniSamyB3
 
Slides13.pdf
byssuser3b4934
 
PCD ?s(MCA)
byguestf07b62f
 
Pcd(Mca)
byguestf07b62f
 
Pcd(Mca)
byguestf07b62f
 

Recently uploaded

PPTX
Time Series Analysis - Weighted (Unequal) Moving Average Method
bySundar B N
 
PDF
Integrated Circuits: Lithography Techniques - Fundamentals and Advanced Metho...
byGS Virdi
 
PDF
Deep Research and Analysis - by Ms. Oceana Wong
byagenticroom
 
PPTX
Photography Pillar 1 The Subject PowerPoint
bymjb77ny
 
PDF
Unit 4_ small scale industries & Entrepreneurship
byNileshKumbhar21
 
PDF
Unit 2: Functions of Management (POSDC.)
byNileshKumbhar21
 
PDF
Unit 1- Basics of Management Cha. of Magmt
byNileshKumbhar21
 
PDF
Rigor, ethics, wellbeing and resilience in the biomedical doctoral journey
byYannis
 
PDF
UGC NET Paper 1 Syllabus | 10 Units Complete Guide for NTA JRF
byNIKHIL K N
 
PPTX
Chapter 3. Pharmaceutical Aids (pharmaceutics)
bySharibJamal
 
PPT
n-1-PMES-Guidelines-for-SY-2025-2026.ppt
bygloriajaneparagas
 
PPTX
G-Protein-Coupled Receptors (GPCRs): Structure, Mechanism, and Functions
byAnoja Kurian
 
PDF
AI Chatbots and Prompt Engineering - by Ms. Oceana Wong
byagenticroom
 
PDF
IMPATT Diodes: Theory, Construction, Operation, and Microwave Applications"
byGS Virdi
 
PDF
Cattolica University - Lab Generative and Agentic AI - Mario Bencivinni
byMario Bencivinni
 
PPTX
kklklklklklklklk;lkpoipor[3rjdkjoe99759893058085
bypreetheshparmar
 
PDF
AI Workflows and Workflow Rhetoric - by Ms. Oceana Wong
byagenticroom
 
PPTX
Time Series Analysis - Method of Simple Moving Average 3 Year and 4 Year Movi...
bySundar B N
 
PPTX
Plant Breeding: Its History and Contribution
bySatyam Sharma
 
PDF
Multimodal and Multimedia AI - by Ms. Oceana Wong
byagenticroom
 
Time Series Analysis - Weighted (Unequal) Moving Average Method
bySundar B N
 
Integrated Circuits: Lithography Techniques - Fundamentals and Advanced Metho...
byGS Virdi
 
Deep Research and Analysis - by Ms. Oceana Wong
byagenticroom
 
Photography Pillar 1 The Subject PowerPoint
bymjb77ny
 
Unit 4_ small scale industries & Entrepreneurship
byNileshKumbhar21
 
Unit 2: Functions of Management (POSDC.)
byNileshKumbhar21
 
Unit 1- Basics of Management Cha. of Magmt
byNileshKumbhar21
 
Rigor, ethics, wellbeing and resilience in the biomedical doctoral journey
byYannis
 
UGC NET Paper 1 Syllabus | 10 Units Complete Guide for NTA JRF
byNIKHIL K N
 
Chapter 3. Pharmaceutical Aids (pharmaceutics)
bySharibJamal
 
n-1-PMES-Guidelines-for-SY-2025-2026.ppt
bygloriajaneparagas
 
G-Protein-Coupled Receptors (GPCRs): Structure, Mechanism, and Functions
byAnoja Kurian
 
AI Chatbots and Prompt Engineering - by Ms. Oceana Wong
byagenticroom
 
IMPATT Diodes: Theory, Construction, Operation, and Microwave Applications"
byGS Virdi
 
Cattolica University - Lab Generative and Agentic AI - Mario Bencivinni
byMario Bencivinni
 
kklklklklklklklk;lkpoipor[3rjdkjoe99759893058085
bypreetheshparmar
 
AI Workflows and Workflow Rhetoric - by Ms. Oceana Wong
byagenticroom
 
Time Series Analysis - Method of Simple Moving Average 3 Year and 4 Year Movi...
bySundar B N
 
Plant Breeding: Its History and Contribution
bySatyam Sharma
 
Multimodal and Multimedia AI - by Ms. Oceana Wong
byagenticroom
 

Declarative Semantics Definition - Term Rewriting

Editor's Notes