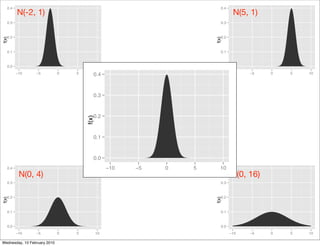
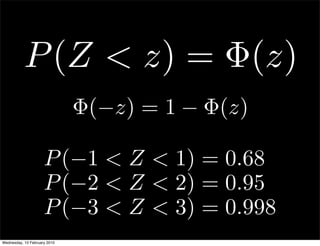The document provides information about an upcoming statistics workshop, an in-class test covering probability and distributions, expectations for the test, guidance on preparing note sheets, and content on the normal distribution including its probability density function, transformations of normal random variables, and the standard normal distribution.