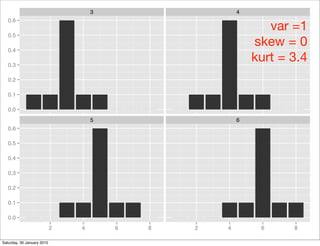
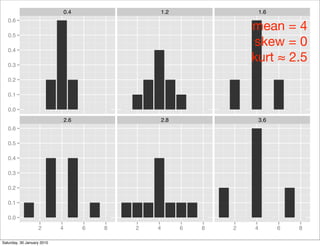
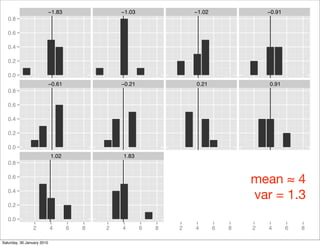
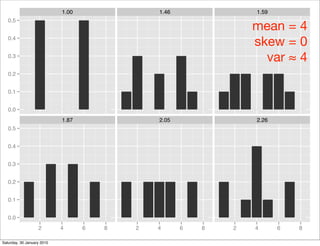
This document contains notes from a Stat310 class on moments. It discusses the definition of moments, including that the mean is the first moment and variance is the second central moment. It provides formulas for the mean, variance, skewness, and kurtosis. Examples of different distributions are shown graphically and their properties discussed, including the binomial and Poisson distributions. The moment generating function is introduced and how it can be used to find the mean and variance. Students are asked to practice computing these properties for different distributions.








![Moments
The ith moment of a random variable is
defined as E(X i) = μ' . The ith central
i
moment is defined as E[(X - E(X)) i] = μ
i
The mean is the ________ moment. The
variance is the ________ moment.
Saturday, 30 January 2010](https://image.slidesharecdn.com/06-moments-100130092732-phpapp02/85/06-Moments-9-320.jpg)