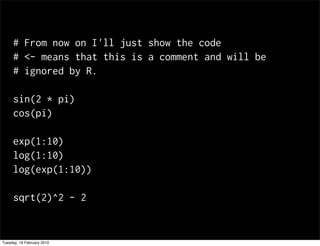
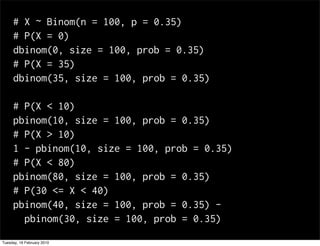
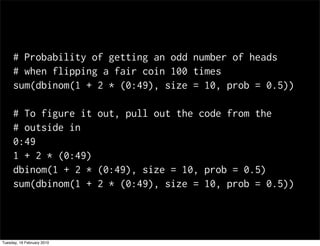
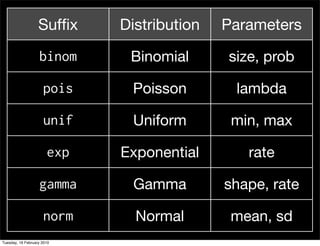
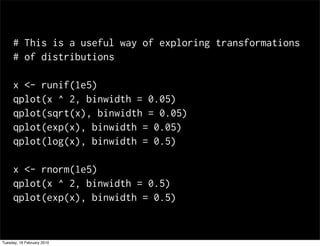
This document contains notes from a statistics course. It discusses upcoming tests and help sessions. It also outlines topics to be covered, including the normal distribution, introduction to R, generating random numbers, and working with probabilities and distributions in R. Examples are provided on calculating probabilities and generating random values from distributions in R.









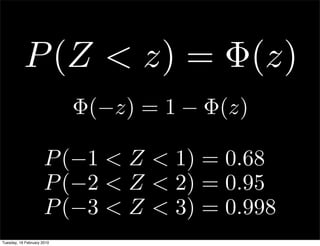


![> 3 + 7
[1] 10
> sqrt(100) + 3 ^ 2
[1] 19
> 1:10
[1] 1 2 3 4 5 6 7 8 9 10
> (1:10) ^ 2
[1] 1 4 9 16 25 36 49 64 81 100
Tuesday, 16 February 2010](https://image.slidesharecdn.com/11-simulation-100216095912-phpapp01/85/11-Simulation-13-320.jpg)