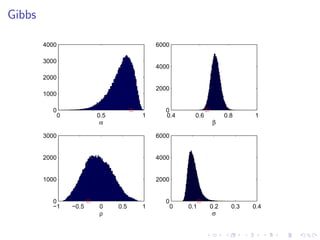
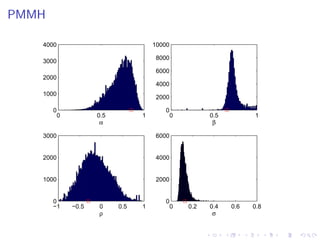
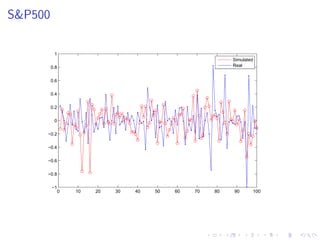
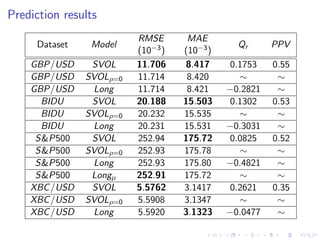
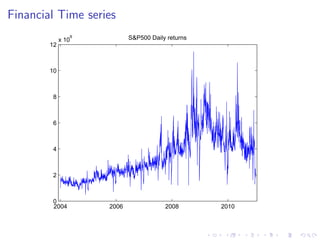
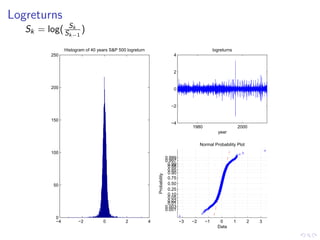
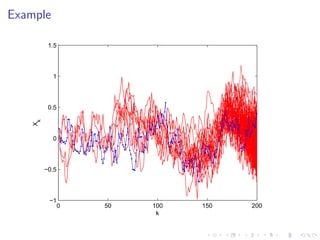
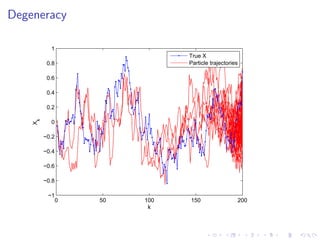
This document summarizes a Bayesian inference method called particle Markov chain Monte Carlo (PMCMC) for estimating parameters in a stochastic volatility model of financial time series. PMCMC combines sequential Monte Carlo (SMC) methods and Markov chain Monte Carlo (MCMC) to sample the parameter posterior distribution. SMC is used to estimate likelihoods and simulate state trajectories, while MCMC proposals are accepted or rejected based on a Metropolis-Hastings ratio involving the estimated likelihoods. The document outlines the stochastic volatility model, parameter estimation using Gibbs sampling, SMC methods for simulation and filtering, and the particle MCMC algorithm for joint simulation of parameters and states.












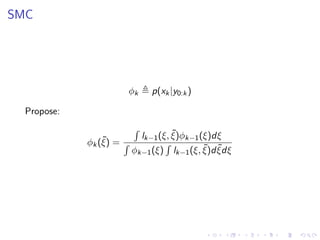











![Implementation
X0 = randn(C,T); theta0 = randn(C,n_theta);
X(:,1) = X0; theta(:,1) = theta0;
for t = 2:M
% Simulationstep
parfor gamma = 2:C % Parallell for-loop
[X(gamma,Nt) theta(gamma,Nt) omega(gamma)] ...
= PMMH_SAMPLER(X(gamma,t), theta(gamma,t), N);
end
% Mergestep
A = randsample(1:C, C, true, omega/sum(omega))
X(:,1:N*t) = X(A,1:N*t);
theta(:,1:t) = theta(A,1:t);
end
A_out = randsample(1:C,1)
tau_out = [X(A_out,:); theta(A_out,:)];](https://image.slidesharecdn.com/pres6-110801063728-phpapp02/85/Bayesian-Inference-on-a-Stochastic-Volatility-model-Using-PMCMC-methods-30-320.jpg)