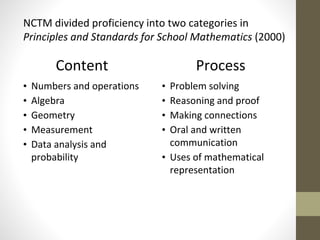
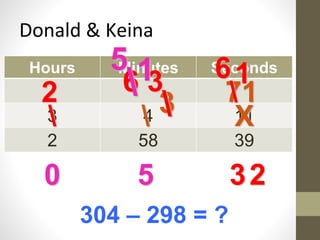
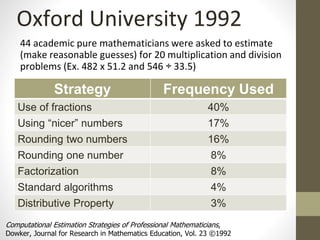
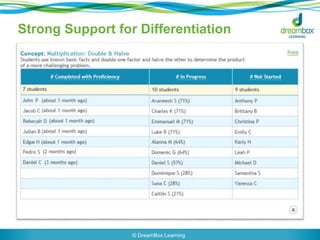
The document outlines the importance of empowering pre-service and new math teachers to effectively use the Common Core State Standards for Mathematics (CCSSM), emphasizing the need for robust mathematical practices in their training. It discusses the historical development of these standards and suggests incorporating reflective writing and low-threshold high-ceiling problems into teacher education to enhance their understanding of mathematical practices. The role of ongoing support for teachers and the connection between content and pedagogy are highlighted as crucial for effective mathematics instruction.

1. Empowering Pre-Service & New Math Teachers
to Use the Common Core Practice Standards
Tuesday, August 26, 2014
Dr. Tim Hudson,
Senior Director of Curriculum Design,
DreamBox Learning
Benjamin Braun,
Associate Professor of Mathematics,
the University of Kentucky
Join our Adaptive Math Learning community: www.edweb.net/adaptivelearning

2. Join our community
Adaptive Math Learning
www.edweb.net/adaptivelearning
• Invitations to upcoming webinars
• Webinar archives and resources
• Online discussions
• CE quizzes for archived webinars
The recording, slides, and
chat log will be posted in the
Webinar Archives folder of
the Community Toolbox.

3. Webinar Tips
• For better audio/video, close other applications
(like Skype) that use bandwidth.
• Maximize your screen for a larger view by using
the link in the upper right corner.
• A CE certificate for today’s webinar will be emailed
to you 24 hours after the live session.
• If you are viewing this as a recording, you will
need to take the CE quiz located in the Webinar
Archives folder of the Community Toolbox.
• Tweeting? Use #edwebchat

4. Empowering Pre-Service &
New Math Teachers to Use the
Common Core Practice
Standards
August 26, 2014

5. Benjamin Braun, PhD
Associate Professor of Mathematics, U of Kentucky
Editor-in-Chief, American Mathematical Society blog “On
Teaching and Learning Mathematics”
Twitter: @BraunMath
Tim Hudson, PhD
Senior Director of Curriculum Design, DreamBox Learning
Former K-12 Mathematics Curriculum Coordinator,
Parkway School District
Twitter: @DocHudsonMath

6. 1970-1990
• “Back to basics” movements in 1970s led to
influential reports arguing in favor of balance
between conceptual and procedural
understanding:
o A Nation at Risk (1983, NCEE)
o An Agenda for Action (1980, NCTM)
• NCTM Standards released in 1989.

7. 2000-2001
• Role of standards-based assessment increased in
early 2000’s with No Child Left Behind.
• At the same time, updated NCTM Standards
released in 2000, and National Research Council
report Adding It Up released in 2001.

8. 2004
• Must read: “The Math Wars,” Alan H.
Schoenfeld, Educational Policy, Vol. 18 No. 1,
January and March 2004, pp. 253-286. (PDF
versions available online.)

9. NCTM divided proficiency into two categories in
Principles and Standards for School Mathematics (2000)
Content
• Numbers and operations
• Algebra
• Geometry
• Measurement
• Data analysis and
probability
Process
• Problem solving
• Reasoning and proof
• Making connections
• Oral and written
communication
• Uses of mathematical
representation

10. NRC emphasized five “strands” of
proficiency in Adding It Up (2001)
• Conceptual understanding: comprehension of
mathematical concepts, operations, and relations
• Procedural fluency: skill in carrying out procedures
flexibly, accurately, efficiently, and appropriately
• Strategic competence: ability to formulate, represent,
and solve mathematical problems
• Adaptive reasoning: capacity for logical thought,
reflection, explanation, and justification
• Productive disposition: habitual inclination to see
mathematics as sensible, useful and worthwhile, coupled
with a belief in diligence and one’s own efficacy

11. Common Core Mathematical
Practice Standards
1. Make sense of problems and persevere in solving
them.
2. Reason abstractly and quantitatively.
3. Construct viable arguments and critique the reasoning
of others.
4. Model with mathematics.
5. Use appropriate tools strategically.
6. Attend to precision.
7. Look for and make use of structure.
8. Look for and express regularity in repeated reasoning.

12. Implications for Pre-service Teachers?
Many (if not most) pre-service teachers at the
elementary, middle, and secondary levels do not
have a robust set of mathematical practices, as
this has not been part of their own educational
experience.

13. Implications for Pre-service Teachers?
This creates a disconnect between content and
methods courses, and also between pre-service
coursework and in-service curriculum and
assessment expectations.

14. Implications for Pre-service Teachers?
Teacher educators, including faculty teaching both
methods and content courses, need to ensure that
pre-service teachers enter the beginning of their
careers with an understanding that mathematical
proficiency extends beyond content.

15. Implications for Pre-service Teachers?
Challenges to incorporating practices in pre-service
teacher courses include balancing
practices and content, effectively training college
faculty (including adjuncts and TAs), and building
quality connections between content and
methods instructors so these courses articulate
well.

16. Implications for Pre-service Teachers?
Even in non-CCSS states, the NRC and NCTM
reports of the past 30+ years have had a major
impact on curriculum and assessment, so this
matters even in non-CCSS states.

17. Implications for Year 1-3 Teachers?
In situations where there has been inadequate
Pre-Service training for mathematics teachers,
new teachers need even more content-specific
support.

18. Implications for Year 1-3 Teachers?
Many schools, districts, and states do not have
adequate mathematics curriculum leadership to
support new math teachers in content-specific
ways.

19. Implications for Year 1-3 Teachers?
New teacher induction and PD often emphasizes
other aspects of teaching instead of curriculum
(i.e., classroom management, parent
communication, or building culture).

20. Implications for Year 1-3 Teachers?
What are math teachers hired to accomplish?
What is mathematics?
How do people learn mathematics?

21. Grant Wiggins
What’s the job of a teacher?
The crying need for a genuine job
description.
grantwiggins.wordpress.com 7-25-14

22. Grant Wiggins
“A real job description would be
written around key learning goals and
Mission-related outcomes.
• What am I expected to cause in students?
• What am I supposed to accomplish?
Whatever the answer, that’s my job.”
grantwiggins.wordpress.com 7-25-14

23. Must Cause 4 Things in Learners
1. greater interest in the subject
and in learning than was there
before, as determined by
observations, surveys, and client
feedback
grantwiggins.wordpress.com 7-25-14

24. Must Cause 4 Things in Learners
2. successful learning related to
key course goals, as reflected in
mutually agreed-upon evidence
grantwiggins.wordpress.com 7-25-14

25. Must Cause 4 Things in Learners
3. greater confidence and feelings
of efficacy as revealed by
student behavior and reports
(and as eventually reflected in
improved results)
grantwiggins.wordpress.com 7-25-14

26. Must Cause 4 Things in Learners
4. a passion and intellectual
direction in each learner as
determined by student-initiated
pursuits, observations, surveys,
and behavior.
grantwiggins.wordpress.com 7-25-14

27. Does Your Mission Obligate
Teachers to Achieve these Goals?
Do Teachers Hired at Your School
Know these are their Goals?
Do Teachers Receive Feedback about
how well they’ve Achieved these Goals?
1. greater interest than was there before
2. successful learning related to key goals
3. greater confidence and feelings of efficacy
4. a passion and intellectual direction
grantwiggins.wordpress.com 7-25-14

28. Two ways to incorporate mathematical
practices in teacher training and
professional development

29. Using Writing Assignments
Pre-service teachers need to write and discuss
mathematical practices explicitly in content
courses. This can’t be “left to the methods
courses” to handle, there must be a dialogue.

30. Using Writing Assignments
One of the best tools we have for this task is
writing assignments.
• Personal writing, e.g reflective essays
• Expository writing, e.g. report on good
contact/practices contact points
• Critical writing, e.g. analyzing practices of
peers

31. Example of a Personal Essay Prompt
There are eight Standards for Mathematical Practice in the
Common Core State Standards for Mathematics. Select at least
three of these standards to consider. For each of the standards
that you select, discuss a situation where you have observed one
of your classmates demonstrating that practice in their work.
This situation might have arisen from in-class group work, from
working with a study group on homework, from hallway
discussions of a problem, etc, but you should discuss a moment
when your classmate was using one of these practices when
working on a mathematical problem. You should explicitly
connect each situation with the written description of the related
practice standard given in the Common Core.

32. Low-threshold high-ceiling problems
• Nothing is better than doing mathematics while
receiving quality feedback for developing good
mathematical practices, which teachers must
have if they are to help others develop them.
• Students need to engage with low-threshold-high-
ceiling (LTHC) problems.
• Open (unsolved) problems in math are a great
source of LTHC problems!

33. K-5 level open problem #1
Fibonacci Primes
• The Fibonacci numbers are
1,1,2,3,5,8,13,21,34,55,... obtained by
adding the two previous numbers to get
the next in the sequence.
• OPEN QUESTION: Are there infinitely
many prime Fibonacci numbers?

34. K-5 level open problem #2
Fermat Primes
• The Fermat numbers are 2^(2^n)+1 for
all non-negative integers n, e.g. 3, 5, 17,
257, 65537,...
• OPEN QUESTION: Are there infinitely
many prime Fermat numbers?

35. K-5 level open problem #3
Collatz Conjecture
• Given a positive integer n, if it is odd
then calculate 3n+1. If it is even,
calculate n/2. Repeat this process with
your new number.
• Example: 1,4,2,1,4,2,1,4,2,1,...
• Example: 5,16,8,4,2,1,...
• OPEN QUESTION: If you start with any
positive integer, does this process always
end by cycling through 1,4,2,1,4,2,1,...?

36. K-5 level open problem #4
Erdos-Strauss Conjecture
• OPEN QUESTION: For every positive
integer n larger than 1, does there exist a
solution to
4/n = 1/x + 1/y + 1/z
using positive integers x, y, and z?
• Example: 4/5 = 1/2 + 1/5 + 1/10

37. Higher-level open problems
• Parity of the partition function
• Irrationality of Euler-Mascheroni constant
• Lagarias’s reformulation of the Riemann
Hypothesis
Many more are available at:
http://en.wikipedia.org/wiki/List_of_conjectures

38. K-5 Level Closed Problem
On day three of the bicycle race, Donald’s
time was:
3 hours, 4 minutes, and 11 seconds.
Keina’s time was:
2 hours, 58 minutes, and 39 seconds.
How long was Keina finished before
Donald crossed the finish line?

39. Donald & Keina
61
Hours Minutes Seconds
71
6 3
3 X
3 4 11
2 58 39
3
2
5 1
0 5 2
304 – 298 = ?

40. Oxford University 1992
44 academic pure mathematicians were asked to estimate
(make reasonable guesses) for 20 multiplication and division
problems (Ex. 482 x 51.2 and 546 ÷ 33.5)
Strategy Frequency Used
Use of fractions 40%
Using “nicer” numbers 17%
Rounding two numbers 16%
Rounding one number 8%
Factorization 8%
Standard algorithms 4%
Distributive Property 3%
Computational Estimation Strategies of Professional Mathematicians,
Dowker, Journal for Research in Mathematics Education, Vol. 23 ©1992

41. Oxford University 1992
44 academic pure mathematicians were asked to estimate
(make reasonable guesses) for 20 multiplication and division
problems (Ex. 482 x 51.2 and 546 ÷ 33.5)
Strategy Frequency Used
Use of fractions 40%
Using “nicer” numbers 17%
Rounding two numbers 16%
Rounding one number 8%
Factorization 8%
Standard algorithms 4%
Distributive Property 3%
Computational Estimation Strategies of Professional Mathematicians,
Dowker, Journal for Research in Mathematics Education, Vol. 23 ©1992

42. Oxford University 1992
“To the person without number sense,
arithmetic is a bewildering territory in
which any deviation from the known
path may rapidly lead to being totally
lost. The person with number
sense…has, metaphorically, an effective
‘cognitive map’ of that same territory.”
Computational Estimation Strategies of Professional Mathematicians,
Dowker, Journal for Research in Mathematics Education, Vol. 23 ©1992

43. Summary
• It is well-established that mathematical proficiency involves
both practices and content.
• All teachers need support in developing skillful approaches to
teaching both mathematical content and practices.
• An excellent way for pre-service and new in-service teachers
to develop their understanding of the practices is to work on
LTHC problems themselves, then reflect on the mathematical
practices they used in their own work.
• Everyone - teachers and students - benefit the most from
receiving quality feedback when developing their content
knowledge and mathematical practices.

44. Q & A

45. Reinventing the Learning Experience
Intelligent Adaptive
Learning™ Engine
• Millions of personalized learning
paths
• Tailored to a student’s
unique needs
Motivating Learning
Environment
• Student Directed, Empowering
• Gaming Fundamentals,
Rewards
Rigorous Elementary
Mathematics PreK-8
• Reporting Aligned to Common
Core State Standards, Texas
TEKS, Virginia SOL, Canada
WNCP, & Canada Ontario
Curriculum Reports
• Standards for
Mathematical
Practice

46. DreamBox Lessons & Virtual Manipulatives
Intelligently adapt & individualize to:
• Students’ own intuitive strategies
• Kinds of mistakes
• Efficiency of strategy
• Scaffolding needed
• Response time
© DreamBox Learning

47. Robust Reporting
© DreamBox Learning

48. Strong Support for Differentiation
© DreamBox Learning

49. DreamBox supports small group and whole
class instructional resources
Interactive white-board lessons
www.dreambox.com/teachertools
© DreamBox Learning

50. Free School-wide Trial! www.dreambox.com

51. Thank you!

52. Join our community
Adaptive Math Learning
www.edweb.net/adaptivelearning
• Invitations to upcoming webinars
• Webinar archives and resources
• Online discussions
• CE quizzes for archived webinars
The recording, slides, and
chat log will be posted in the
Webinar Archives folder of
the Community Toolbox.

53. Thank you to our sponsor:
www.dreambox.com

54. Stay tuned for information on upcoming webinars!
Join our Adaptive Math Learning community for an invitation:
www.edweb.net/adaptivelearning