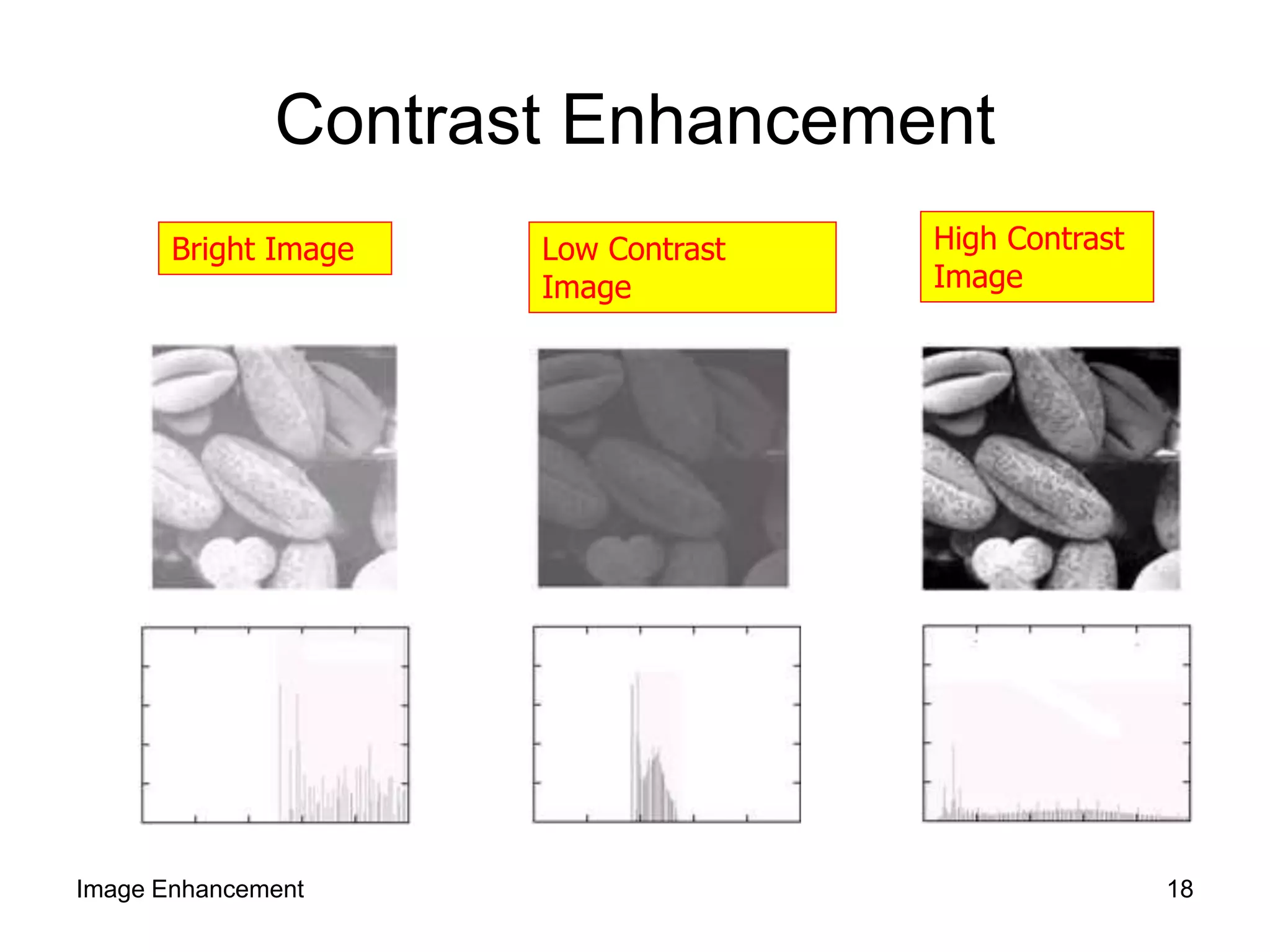
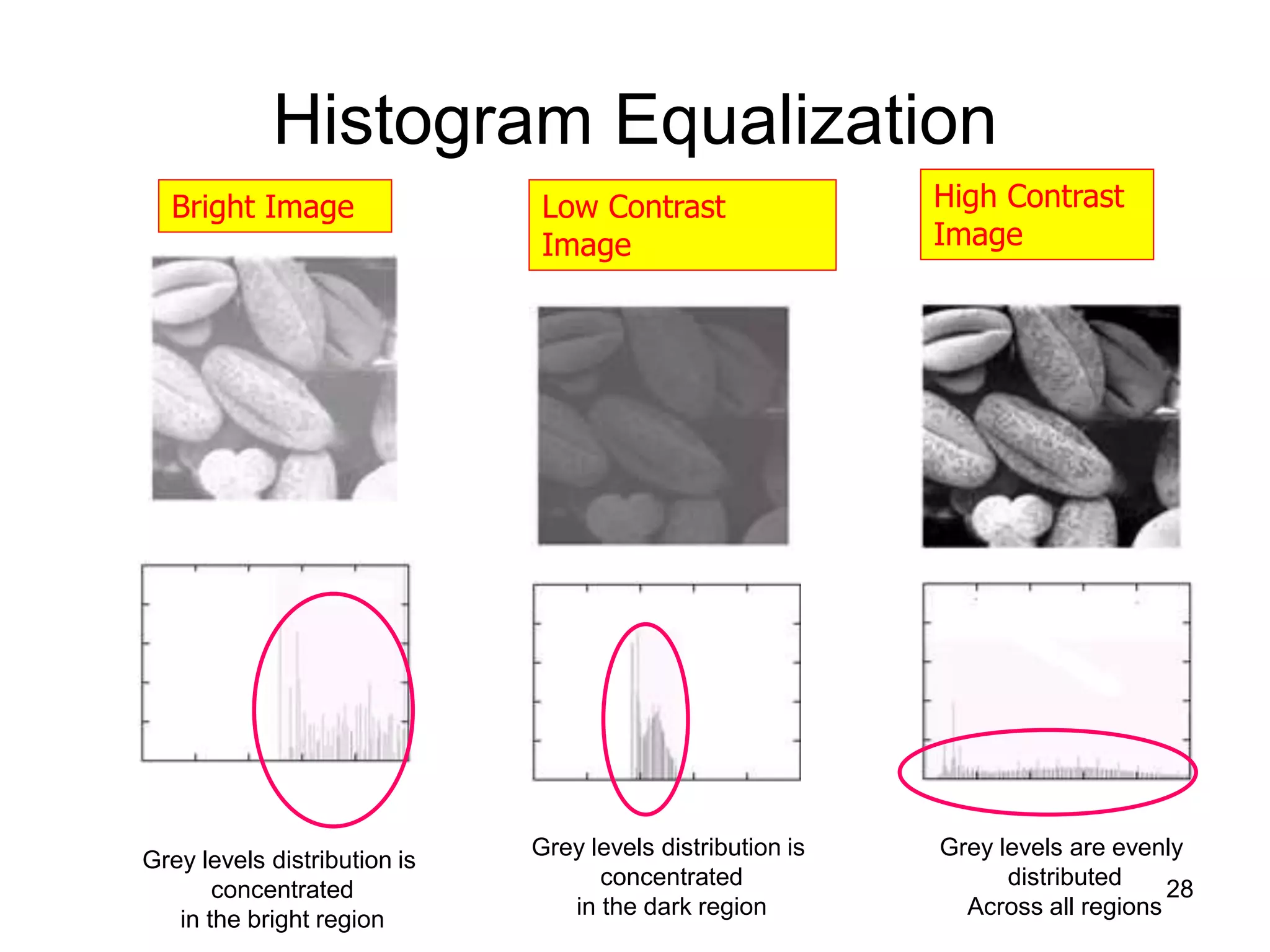
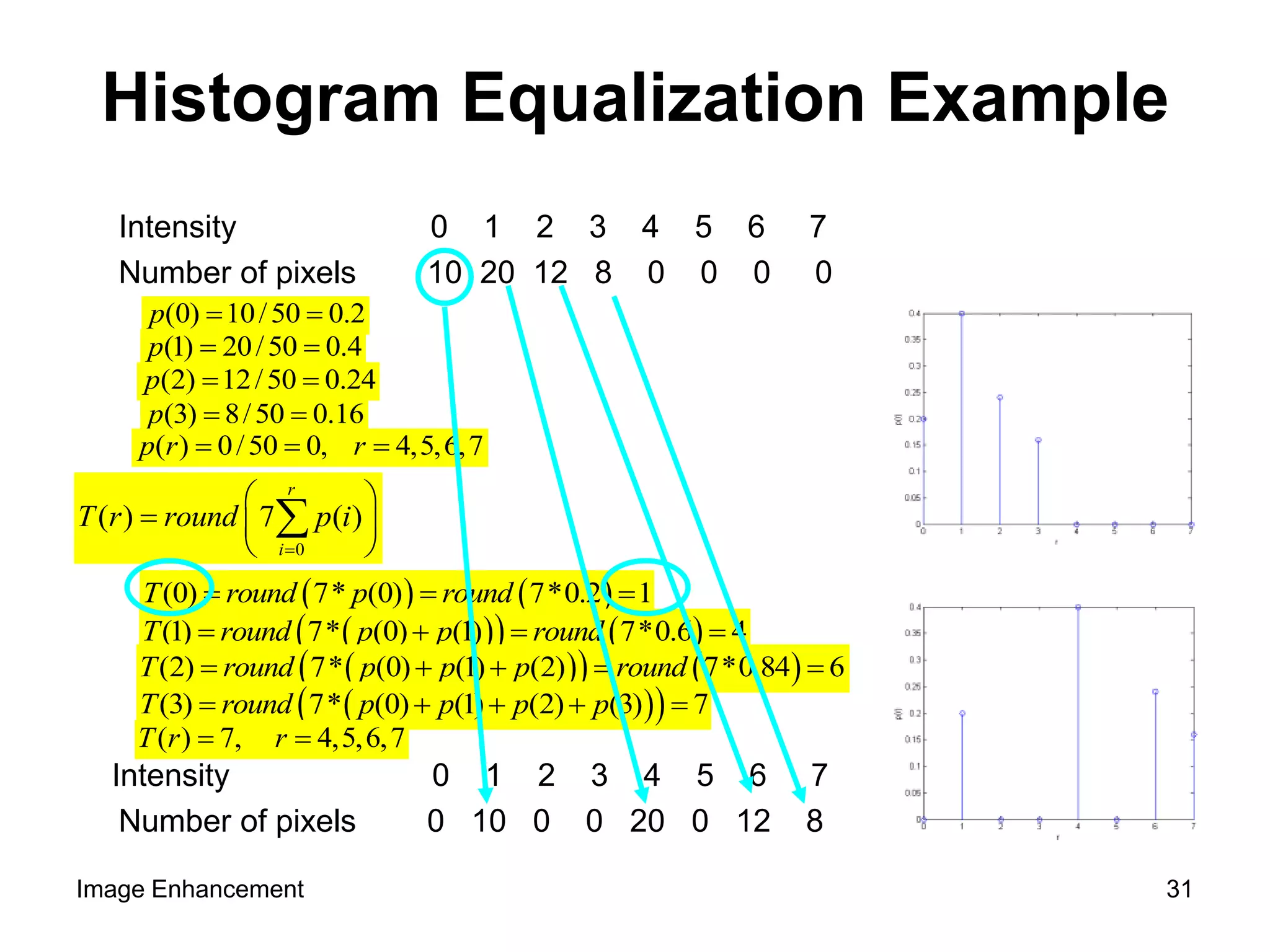
The document discusses image enhancement techniques for noise removal and contrast enhancement. It describes using average and median filters to remove noise, and histogram equalization to enhance contrast. Examples are provided to demonstrate noise removal using an average filter and median filter on sample images with added salt and pepper noise.

1. Image Enhancement
Noise Removal and Contrast Enhancement
Elsayed Hemayed

2. Overview
• Noise removal
– Using average filter
– Using Median filter
• Contrast Enhancement
– Specific enhancement techniques
– Histogram equalization
Image Enhancement 2

3. 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 90 90 90 90 90 0 0
0 0 0 90 90 90 90 90 0 0
0 0 0 90 90 90 90 90 0 0
0 0 0 90 0 90 90 90 0 0
0 0 0 90 90 90 90 90 0 0
0 0 0 0 0 0 0 0 0 0
0 0 90 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 90 90 90 90 90 0 0
0 0 0 90 90 90 90 90 0 0
0 0 0 90 90 90 90 90 0 0
0 0 0 90 0 90 90 90 0 0
0 0 0 90 90 90 90 90 0 0
0 0 0 0 0 0 0 0 0 0
0 0 90 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
],[],[],[
,
lnkmflkgnmh
lk
 
[.,.]h[.,.]f
Noise removal using average filter
111
111
111
],[g 
3

4. 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 90 90 90 90 90 0 0
0 0 0 90 90 90 90 90 0 0
0 0 0 90 90 90 90 90 0 0
0 0 0 90 0 90 90 90 0 0
0 0 0 90 90 90 90 90 0 0
0 0 0 0 0 0 0 0 0 0
0 0 90 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 10
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 90 90 90 90 90 0 0
0 0 0 90 90 90 90 90 0 0
0 0 0 90 90 90 90 90 0 0
0 0 0 90 0 90 90 90 0 0
0 0 0 90 90 90 90 90 0 0
0 0 0 0 0 0 0 0 0 0
0 0 90 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
[.,.]h[.,.]f
111
111
111
],[g 
],[],[],[
,
lnkmflkgnmh
lk
  4

5. 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 90 90 90 90 90 0 0
0 0 0 90 90 90 90 90 0 0
0 0 0 90 90 90 90 90 0 0
0 0 0 90 0 90 90 90 0 0
0 0 0 90 90 90 90 90 0 0
0 0 0 0 0 0 0 0 0 0
0 0 90 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 10 20
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 90 90 90 90 90 0 0
0 0 0 90 90 90 90 90 0 0
0 0 0 90 90 90 90 90 0 0
0 0 0 90 0 90 90 90 0 0
0 0 0 90 90 90 90 90 0 0
0 0 0 0 0 0 0 0 0 0
0 0 90 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
[.,.]h[.,.]f
111
111
111
],[g 
],[],[],[
,
lnkmflkgnmh
lk
  5

6. 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 90 90 90 90 90 0 0
0 0 0 90 90 90 90 90 0 0
0 0 0 90 90 90 90 90 0 0
0 0 0 90 0 90 90 90 0 0
0 0 0 90 90 90 90 90 0 0
0 0 0 0 0 0 0 0 0 0
0 0 90 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 10 20 30
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 90 90 90 90 90 0 0
0 0 0 90 90 90 90 90 0 0
0 0 0 90 90 90 90 90 0 0
0 0 0 90 0 90 90 90 0 0
0 0 0 90 90 90 90 90 0 0
0 0 0 0 0 0 0 0 0 0
0 0 90 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
[.,.]h[.,.]f
111
111
111
],[g 
],[],[],[
,
lnkmflkgnmh
lk
  6

7. 0 10 20 30 30
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 90 90 90 90 90 0 0
0 0 0 90 90 90 90 90 0 0
0 0 0 90 90 90 90 90 0 0
0 0 0 90 0 90 90 90 0 0
0 0 0 90 90 90 90 90 0 0
0 0 0 0 0 0 0 0 0 0
0 0 90 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
[.,.]h[.,.]f
111
111
111
],[g 
],[],[],[
,
lnkmflkgnmh
lk
  7

8. 0 10 20 30 30
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 90 90 90 90 90 0 0
0 0 0 90 90 90 90 90 0 0
0 0 0 90 90 90 90 90 0 0
0 0 0 90 0 90 90 90 0 0
0 0 0 90 90 90 90 90 0 0
0 0 0 0 0 0 0 0 0 0
0 0 90 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
[.,.]h[.,.]f
111
111
111
],[g 
?
],[],[],[
,
lnkmflkgnmh
lk
  8

9. 0 10 20 30 30
50
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 90 90 90 90 90 0 0
0 0 0 90 90 90 90 90 0 0
0 0 0 90 90 90 90 90 0 0
0 0 0 90 0 90 90 90 0 0
0 0 0 90 90 90 90 90 0 0
0 0 0 0 0 0 0 0 0 0
0 0 90 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
[.,.]h[.,.]f
111
111
111
],[g 
?
],[],[],[
,
lnkmflkgnmh
lk
  9

10. 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 90 90 90 90 90 0 0
0 0 0 90 90 90 90 90 0 0
0 0 0 90 90 90 90 90 0 0
0 0 0 90 0 90 90 90 0 0
0 0 0 90 90 90 90 90 0 0
0 0 0 0 0 0 0 0 0 0
0 0 90 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 10 20 30 30 30 20 10
0 20 40 60 60 60 40 20
0 30 60 90 90 90 60 30
0 30 50 80 80 90 60 30
0 30 50 80 80 90 60 30
0 20 30 50 50 60 40 20
10 20 30 30 30 30 20 10
10 10 10 0 0 0 0 0
[.,.]h[.,.]f
111
111
111
],[g 
],[],[],[
,
lnkmflkgnmh
lk
  10

11. Salt and Pepper Noise
128 128 128 128 128 128 128 128 128 128
128 128 128 128 128 128 128 128 128 128
128 128 128 128 128 128 128 128 128 128
128 128 128 128 128 128 128 128 128 128
128 128 128 128 128 128 128 128 128 128
128 128 128 128 128 128 128 128 128 128
128 128 128 128 128 128 128 128 128 128
128 128 128 128 128 128 128 128 128 128
128 128 128 128 128 128 128 128 128 128
128 128 128 128 128 128 128 128 128 128
X
128 128 255 0 128 128 128 128 128 128
128 128 128 128 0 128 128 128 128 0
128 128 128 128 128 128 128 128 128 128
128 128 0 128 128 128 128 128 128 128
128 128 128 128 128 128 128 128 128 128
128 128 128 128 128 128 128 128 128 128
128 128 128 128 128 128 128 128 128 128
0 128 128 128 128 255 128 128 128 128
128 128 128 128 128 128 128 128 128 255
128 128 128 128 128 128 128 255 128 128
Y
Noise level p=0.1 means that approximately
10% of pixels are contaminated by
salt or pepper noise (highlighted by red color)

12. Median Filter
• In a set of ordered values, the median is
the central value.
• The idea is to replace the current point in
the image by the median of the brightness
in its neighborhood
• It eliminate salt and pepper noise
Example ]56,55,54,255,52,0,50[y

54)( ymedian

]255,56,55,54,52,50,0[y

sorted

13. 2D Numerical Example
225 225 225 226 226 226 226 226
225 225 255 226 226 226 225 226
226 226 225 226 0 226 226 255
255 226 225 0 226 226 226 226
225 255 0 225 226 226 226 255
255 225 224 226 226 0 225 226
226 225 225 226 255 226 226 228
226 226 225 226 226 226 226 226
0 225 225 226 226 226 226 226
225 225 226 226 226 226 226 226
225 226 226 226 226 226 226 226
226 226 225 225 226 226 226 226
225 225 225 225 226 226 226 226
225 225 225 226 226 226 226 226
225 225 225 226 226 226 226 226
226 226 226 226 226 226 226 226
Y X
^
Sorted: [0, 0, 0, 225, 225, 225, 226, 226, 226]

14. Image Example
3-by-3 window 5-by-5 window
clean
noisy
(p=0.2)

15. • Median smoothing :
– Advantages:
• not affected by individual noise spikes
• does not blur edges much
• can be applied iteratively.
– Main disadvantage of median filtering in a
rectangular neighborhood
• is its damaging of thin lines and sharp corners
in the image -- this can be avoided if another
shape of neighborhood is used.
Eliminate Salt and Pepper Noise

16. • Median smoothing :
– If horizontal/vertical lines need preserving a
neighborhood such as the following can be
used
X
Eliminate Salt and Pepper Noise

17. Original
Image
3x3
averaging
filter
Salt and
Pepper
noise
Added
3x3 median
filter
Eliminate Salt and Pepper Noise
Example

18. Contrast Enhancement
Bright Image Low Contrast
Image
High Contrast
Image
Image Enhancement 18

19. Contrast Enhancement
• Negative transformation
• Brightness thresholding
• Gamma correction
• Contrast Stretching
–linear transform
–Log transform
• Grey level slicing
• Histogram equalization
Image Enhancement 19

20. Negative Transformation
s = 255 - r
Image Enhancement 20

21. Brightness Thresholding
Image Enhancement 21

22. Gamma Correction

inout cVV 
Increasing
gamma
Image Enhancement 22

23. Gamma Correction Examples
c = 1
6.0
4.0 3.0
Original
image

inout cVV 
Image Enhancement 23

24. Gamma Correction Examples
c = 1
3
4 5
Original
image

inout cVV 
Image Enhancement 24

25. Contrast Stretching using linear transform
original image after processing
Image Enhancement 25

26. Contrast Stretching using log transform
original image after processing
Image Enhancement 26

27. Grey Level Slicing
original image after processing
Another possibility for slicing …
what would be the effect?
Image Enhancement 27

28. Histogram Equalization
Bright Image Low Contrast
Image
High Contrast
Image
Grey levels distribution is
concentrated
in the bright region
Grey levels distribution is
concentrated
in the dark region
Grey levels are evenly
distributed
Across all regions
28

29. Histogram Equalization
f
p(r)
Image Enhancement 29

30. The Cumulative Histogram
Number of pixels with intensity
( ) 255
Total number of pixels
i r
T r round
 
  
 
0 255r 
0
255 ( )
r
i
round p i

 
  
 

0
Number of pixels with intensity
255
Total number of pixels
r
i
i
round

 
  
 

r
T(r)
r
Image Enhancement 30

31. Histogram Equalization Example
Intensity 0 1 2 3 4 5 6 7
Number of pixels 10 20 12 8 0 0 0 0
Intensity 0 1 2 3 4 5 6 7
Number of pixels 0 10 0 0 20 0 12 8
(0) 10/50 0.2p  
(1) 20/50 0.4p  
(2) 12/50 0.24p  
(3) 8/50 0.16p  
( ) 0/50 0, 4,5,6,7p r r  
0
( ) 7 ( )
r
i
T r round p i

 
  
 

   (0) 7* (0) 7*0.2 1T round p round  
    (1) 7* (0) (1) 7*0.6 4T round p p round   
    (2) 7* (0) (1) (2) 7*0.84 6T round p p p round    
  (3) 7* (0) (1) (2) (3) 7T round p p p p    
( ) 7, 4,5,6,7T r r 
Image Enhancement 31

32. Histogram Equalization Example 1
Image Enhancement 32

33. Histogram Equalization Example 2
33

34. Summary
• Noise removal
– Using average filter
– Using Median filter
• Contrast Enhancement
– Specific enhancement techniques
– Histogram equalization
Image Enhancement 34