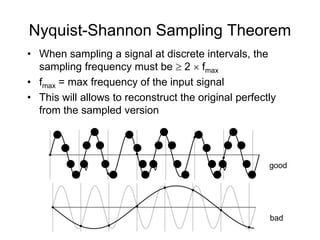
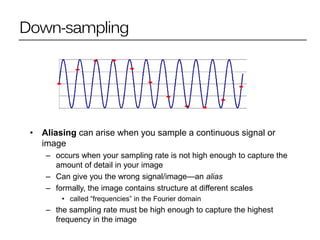
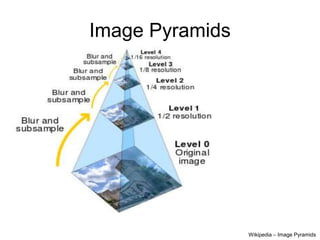
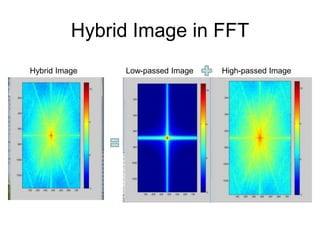
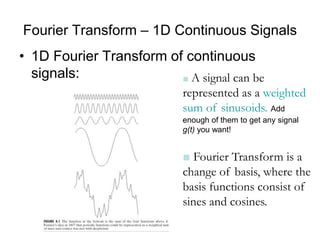
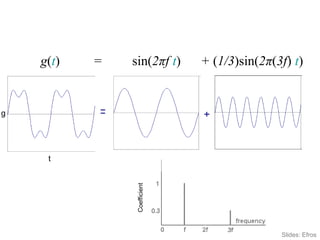
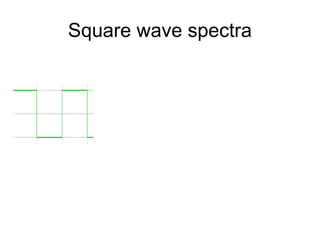
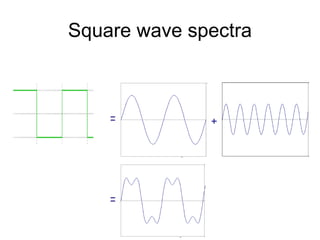
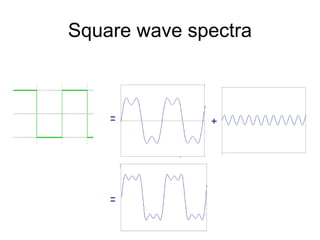
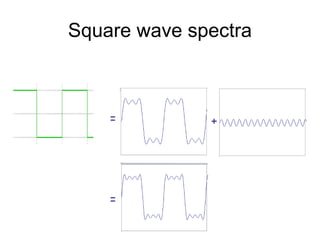
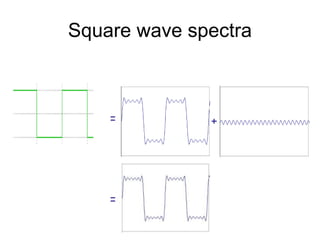
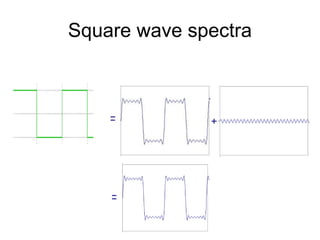
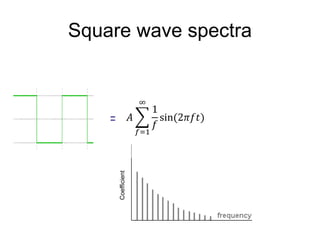
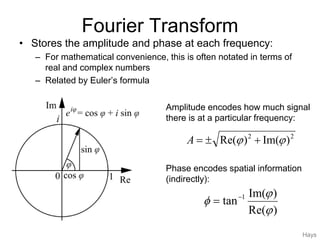
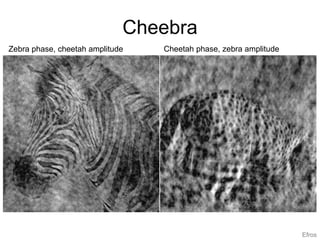
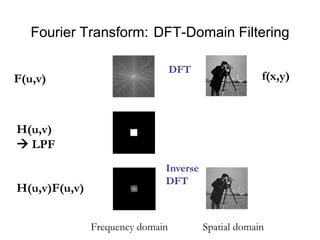
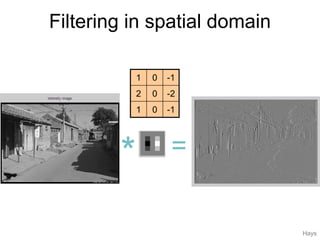
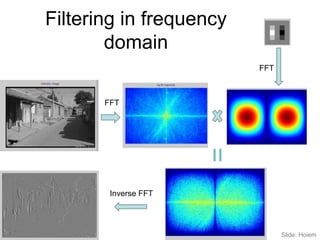
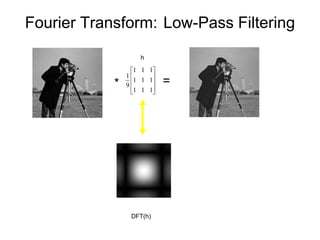
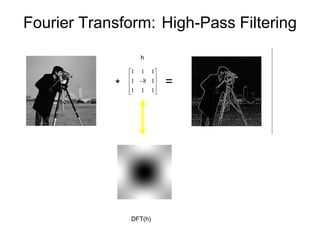
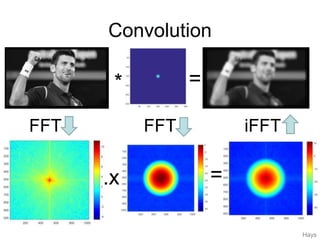
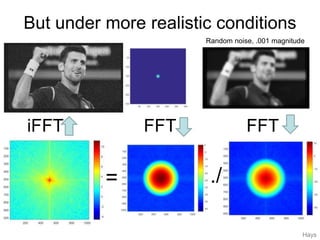
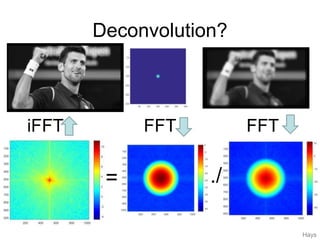
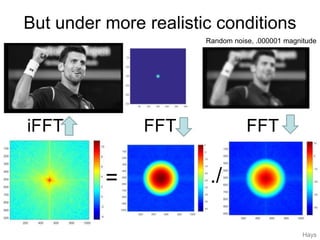
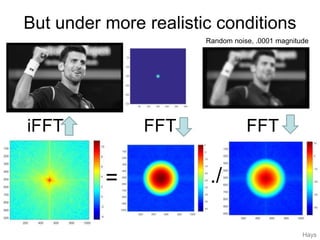
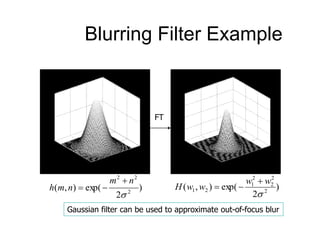
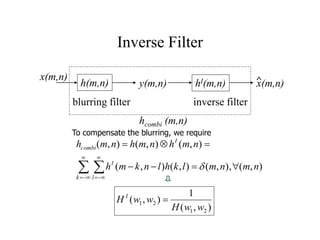
1. Image filtering can be performed in either the spatial or frequency domain using the Fourier transform. Low-pass filtering in the frequency domain removes high frequency components which can reduce aliasing when downsampling images. 2. Deconvolution aims to reverse the effects of blurring by dividing the Fourier transform of an image by the Fourier transform of the blurring filter, but this amplifies noise. Pseudoinverse filtering handles zeros in the blurring filter to improve results. 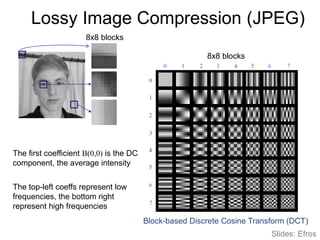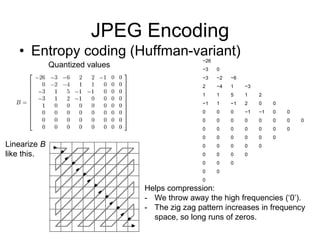3. JPEG compression transforms image blocks to the frequency domain via DCT, quantizes and discards high frequency coefficients, and entropy codes the results to achieve high compression ratios with minimal perceived quality loss.

1. Image Filtering
(Frequency Domain)
Elsayed Hemayed

2. Overview
• Thinking in Frequency
– Image Scaling
– Hybrid Image
• Fourier Transform
• Filtering in Spatial/Frequency Domain
• De-convolution
• Image De-blurring
• Image Compression

3. Image Scaling
This image is too big to
fit on the screen. How
can we reduce it?
How to generate a half-
sized version?

4. Image sub-sampling
Throw away every other row and
column to create a 1/2 size image
- called image sub-sampling
1/4
1/8

5. Image sub-sampling
1/4 (2x zoom) 1/8 (4x zoom)
Why does this look so bad?
1/2

6. • 1D example (sinewave):
Source: S. Marschner
Aliasing problem

7. Source: S. Marschner
• 1D example (sinewave):
Aliasing problem

8. Source: A. Efros
Aliasing in graphics

9. Aliasing in video
Slide by Steve Seitz

10. Videos
[YouTube; JoinBuzzirk; phrancque]
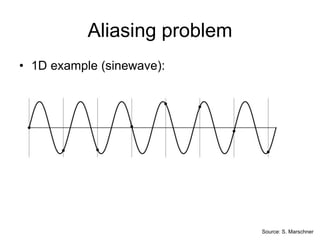
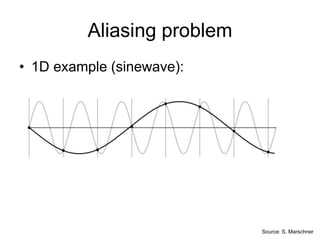
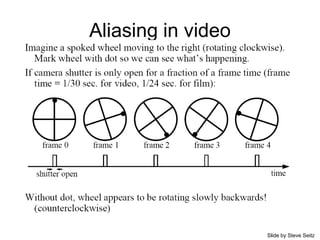
Helicopter flying with no blades spinning !wheels spinning backwards

11. • When sampling a signal at discrete intervals, the
sampling frequency must be  2  fmax
• fmax = max frequency of the input signal
• This will allows to reconstruct the original perfectly
from the sampled version
good
bad
v v v
Nyquist-Shannon Sampling Theorem

12. Down-sampling
• Aliasing can arise when you sample a continuous signal or
image
– occurs when your sampling rate is not high enough to capture the
amount of detail in your image
– Can give you the wrong signal/image—an alias
– formally, the image contains structure at different scales
• called “frequencies” in the Fourier domain
– the sampling rate must be high enough to capture the highest
frequency in the image

13. How to fix aliasing?
Solutions?

14. Better sensors
Solutions:
• Sample more often

15. Anti-aliasing
Solutions:
• Sample more often
• Get rid of all frequencies that are greater
than half the new sampling frequency
– Will lose information
– But it’s better than aliasing
– Apply a smoothing (low pass) filter
Hays

16. Algorithm for downsampling by
factor of 2
1. Start with image(h, w)
2. Apply low-pass filter
im_blur = imfilter( image, fspecial(‘gaussian’, 7, 1) )
3. Sample every other pixel
im_small = im_blur( 1:2:end, 1:2:end );
This way we get rid of all frequencies that are greater
than half the new sampling frequency
Hays

17. Subsampling with Gaussian pre-filtering
G 1/4
G 1/8
Gaussian 1/2
Solution: filter the image, then subsample
• Filter size should double for each ½ size reduction.

18. Subsampling with Gaussian pre-filtering
Gaussian 1/2 G 1/4 (2x zoom) G 1/8 (4x zoom)

19. Image sub-sampling
1/4 (2x zoom) 1/8 (4x zoom)1/2

20. Image Pyramids
Wikipedia – Image Pyramids

21. Why do we get different, distance-
dependent interpretations of hybrid
images?
?
Hays

22. Application: Hybrid Images
A. Oliva, A. Torralba, P.G. Schyns, SIGGRAPH 2006
When we see an image from far away, we are effectively subsampling it!

23. Hybrid Images
• A. Oliva, A. Torralba, P.G. Schyns,
“Hybrid Images,” SIGGRAPH 2006
Hays

24. Hybrid Image in FFT
Hybrid Image Low-passed Image High-passed Image

25. Fourier Transform – 1D Continuous Signals
• 1D Fourier Transform of continuous
signals: ■ A signal can be
represented as a weighted
sum of sinusoids. Add
enough of them to get any signal
g(t) you want!
■ Fourier Transform is a
change of basis, where the
basis functions consist of
sines and cosines.

26. g(t) = sin(2πf t) + (1/3)sin(2π(3f) t)
= +
Slides: Efros
Coefficient
t
g

27. Square wave spectra

28. = +
=
Square wave spectra

29. = +
=
Square wave spectra

30. = +
=
Square wave spectra

31. = +
=
Square wave spectra

32. = +
=
Square wave spectra

33. =
Square wave spectra
Coefficient
𝐴
𝑓=1
∞
1
𝑓
sin(2𝜋𝑓𝑡)

34. 2D DFT – Power Spectra
Three sinusoidal patterns, their frequency transforms, and their sum.
The frequency increases with radius ρ, and the orientation depends
on the angle θ. Origin is in the centre of the image.

35. Basis Reconstruction
Danny Alexander

36. Fourier Transform
• Stores the amplitude and phase at each frequency:
– For mathematical convenience, this is often notated in terms of
real and complex numbers
– Related by Euler’s formula
22
)Im()Re(  A
)Re(
)Im(
tan 1


 

Hays
Phase encodes spatial information
(indirectly):
Amplitude encodes how much signal
there is at a particular frequency:

37. What about phase?
Efros

38. What about phase?
Amplitude Phase
Efros

39. What about phase?
Efros

40. What about phase?
Amplitude Phase
Efros

41. Think-Pair-Share
• In Fourier space, where is more of the
information that we see in the visual
world?
– Amplitude
– Phase

42. Cheebra
Zebra phase, cheetah amplitude Cheetah phase, zebra amplitude
Efros

43. • The frequency amplitude of natural images
are quite similar
– Heavy in low frequencies, falling off in high
frequencies
– Will any image be like that, or is it a property
of the world we live in?
• Most information in the image is carried in
the phase, not the amplitude
Efros

44. Fourier Transform: Properties
■ Linearity
■ Convolution
■ Separable functions
( , ) ( , ) ( , ) ( , )af x y bg x y aF u v bG u v  
( , )* ( , ) ( , ) ( , )f x y g x y F u v G u v
( , ) ( , ) ( , )* ( , )f x y g x y F u v G u v
( , ) ( ) ( ) ( , ) ( ) ( )f x y f x f y F u v F u F v  
2D Fourier Transform can be implemented
as a sequence of two 1D Fourier Transform
operations.

45. Fourier Transform: DFT-Domain Filtering
Frequency domain Spatial domain
H(u,v)
 LPF
f(x,y)F(u,v)
H(u,v)F(u,v)
DFT
Inverse
DFT

46. Filtering in spatial domain
-101
-202
-101
* =
Hays

47. Filtering in frequency
domain
FFT
FFT
Inverse FFT
=
Slide: Hoiem

48. Fourier Transform: Low-Pass Filtering
81x8161x61 121x121

49. Fourier Transform: Low-Pass Filtering
1 1 1
1
1 1 1
9
1 1 1
 
 
 
  
* =
DFT(h)
h

50. Fourier Transform: High-Pass Filtering
* =
1 1 1
1 8 1
1 1 1
 
  
  
DFT(h)
h

51. Low and High Pass filtering

52. Removing frequency bands
Brayer

53. Is convolution invertible?
• If convolution is just multiplication in the
Fourier domain, isn’t deconvolution just
division?
• Sometimes, it clearly is invertible (e.g. a
convolution with an identity filter)
• In one case, it clearly isn’t invertible (e.g.
convolution with an all zero filter)
• What about for common filters like a
Gaussian?

54. Convolution
* =
FFT FFT
.x =
iFFT
Hays

55. Deconvolution?
iFFT FFT
./=
FFT
Hays

56. But under more realistic conditions
iFFT FFT
./=
FFT
Random noise, .000001 magnitude
Hays

57. But under more realistic conditions
iFFT FFT
./=
FFT
Random noise, .0001 magnitude
Hays

58. But under more realistic conditions
iFFT FFT
./=
FFT
Random noise, .001 magnitude
Hays

59. Image Deblurring
• Where does blur come from?
– Optical blur: camera is out-of-focus
– Motion blur: camera or object is moving
• Why do we need deblurring?
– Visually annoying
– Wrong target for compression
– Bad for analysis
– Numerous applications

60. h(m,n) +x(m,n) y(m,n)
),( nmw
• Linear degradation model
),( nmh blurring filter
),0(~),( 2
wNnmw  additive white Gaussian noise
Modeling Blurring Process

61. Blurring Filter Example
)
2
exp(),( 2
2
2
2
1
21

ww
wwH

)
2
exp(),( 2
22

nm
nmh


FT
Gaussian filter can be used to approximate out-of-focus blur

62. Blurring Filter Example (Con’t)
),( 21 wwH
FT
Motion blurring can be approximated by 1D low-pass filter along the moving direction
),( nmh

63. Inverse Filter
h(m,n)
blurring filter
hI(m,n)
x(m,n)
y(m,n)
inverse filter
 






k l
I
I
combi
nmnmlkhlnkmh
nmhnmhnmh
),(),,(),(),(
),(),(),(

),(
1
),(
21
21
wwH
wwH I

To compensate the blurring, we require
hcombi (m,n)
x(m,n)^

64. Inverse Filtering (Con’t)
h(m,n) +x(m,n) y(m,n)
),( nmw
hI(m,n)
inverse filter
x(m,n)^
Spatial:
),()),(),(),((),(),(),(ˆ nmhnmwnmhnmxnmhnmynmx II

Frequency:
),(
),(
),(
),(
),(),(),(
),(),(),(ˆ
21
21
21
21
212121
212121
wwH
wwW
wwX
wwH
wwWwwHwwX
wwHwwYwwX I



amplified noise

65. Image Example
Q: Why does the amplified noise look so bad?
A: zeros in H(w1,w2) correspond to poles in HI (w1,w2)
motion blurred image
at BSNR of 40dB
deblurred image after
inverse filtering

66. Pseudo-inverse Filter
Basic idea:
To handle zeros in H(w1,w2), we treat them separately
when performing the inverse filtering









|),(|0
|),(|
),(
1
),(
21
21
2121
wwH
wwH
wwHwwH

67. Image Example
motion blurred image deblurred image after
Pseudo-inverse filtering
(=0.1)

68. Compression
• How is it that a 4MP image can be
compressed to a few hundred KB without
a noticeable change?

69. Lossy Image Compression (JPEG)
Block-based Discrete Cosine Transform (DCT)
Slides: Efros
The first coefficient B(0,0) is the DC
component, the average intensity
The top-left coeffs represent low
frequencies, the bottom right
represent high frequencies
8x8 blocks
8x8 blocks

70. JPEG Encoding
• Entropy coding (Huffman-variant)
Quantized values
Linearize B
like this.
Helps compression:
- We throw away the high frequencies (‘0’).
- The zig zag pattern increases in frequency
space, so long runs of zeros.
−26
−3 0
−3 −2 −6
2 −4 1 −3
1 1 5 1 2
−1 1 −1 2 0 0
0 0 0 −1 −1 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0
0 0 0 0
0 0 0
0 0
0

71. JPEG Compression Summary
• Convert image to YCrCb
• Subsample color by factor of 2
– People have bad resolution for color
• Split into blocks (8x8, typically), subtract 128
• For each block
– Compute DCT coefficients
– Coarsely quantize
• Many high frequency components will become zero
– Encode (with run length encoding and then Huffman
coding for leftovers)
http://en.wikipedia.org/wiki/YCbCr
http://en.wikipedia.org/wiki/JPEG

72. Summary
• Thinking in Frequency
– Image Scaling
– Hybrid Image
• Fourier Transform
• Filtering in Spatial/Frequency Domain
• De-convolution
• Image De-blurring
• Image Compression