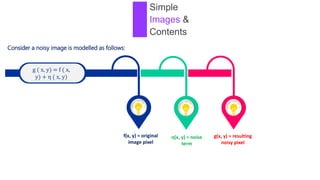
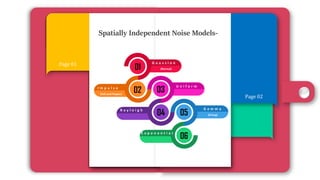
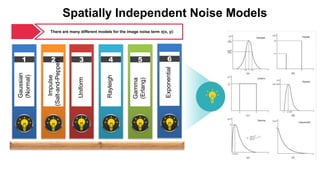
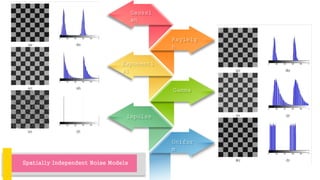
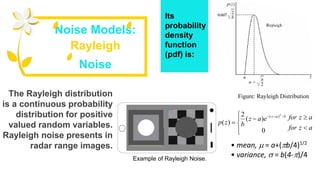
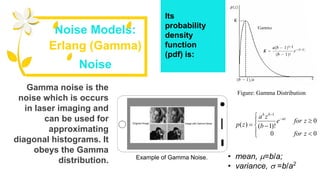
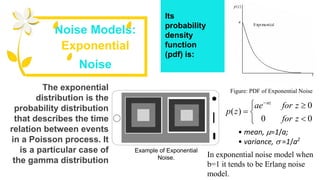
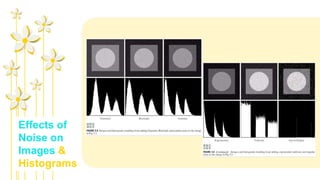
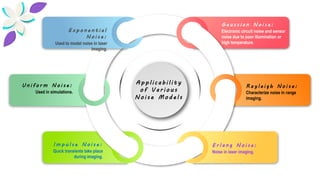
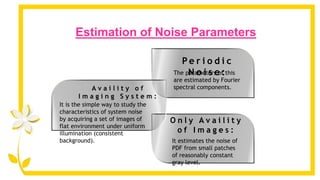
1) The document discusses various types of noise models that can affect digital images, including spatially independent noise models like Gaussian, impulse, uniform, Rayleigh, gamma, and exponential noise. 2) Spatially dependent noise models include periodic noise, which can be reduced via frequency domain filtering. 3) The parameters of different noise models can be estimated from small patches of images, by acquiring images of a flat surface under uniform lighting, or from the Fourier spectrum of periodic noise. Understanding noise models is important for image denoising.

1. Course Title: Pattern Recognition & Image Processing
Course Code: CSE-411

2. 1
2
3
4
5 6
7
8
9
1
0
Contents
Source of Image
Noise
Introduction
Simple Images &
Contents
Noise Model
Spatially Independent
Noise Models
Effects of Noise on
Images & Histograms
Spatially Dependent
Noise Models
Estimation of Noise
Parameters
Applicability of
Various Noise
Models
Conclusion

3. Noise is a disturbance of the image data (projection of
the scene) by image acquisition or the transmission of
images.
We may define noise to be any degradation in the image
signal.
Cleaning an image corrupted by noise is thus an
important area of image restoration.
Noises are mostly implemented in MATLAB.

4. 모바일 이미지
Source of Image Noise
Error occurs in image signal, while an image
is being sent
electronically from one place to another .
Sensor Heat: while clicking an image
ISO Factor: ISO number indicates how quickly
a camera’s sensor absorbs , light , higher ISO
used mare chance of noticeable noise
By memory cell failure.

5. g ( x, y) = f ( x,
y) + η ( x, y)
f(x, y) = original
image pixel
η(x, y) = noise
term
g(x, y) = resulting
noisy pixel
Simple
Images &
Contents
Consider a noisy image is modelled as follows:

6. Page 04
Page 03
Page 02
Page 01
Noise Models
There are several ways that noise
can be introduced into an image,
depending on how the image is
created.

7. Page 02
Page 01
2 Spatially Dependent Noise Model
1 Spatially Independent Noise Models

8. Page 01
Page 01
Page 02
Spatially Independent Noise Models-

9. Page 01
Page 02
Page 02
P e r i o d i c N o i s e
Spatially
Dependent Noise
Model

10. Spatially Independent Noise Models
1 2 3 4 5 6
Gaussian
(Normal)
Impulse
(Salt-and-Pepper)
Uniform
Rayleigh
Gamma
(Erlang)
Exponential
There are many different models for the image noise term η(x, y):

11. Unifor
m
Impulse
Gamma
Exponenti
al
Rayleig
h
Gaussi
an
Spatially Independent Noise Models

12. The Gaussian noise, also
called normal noise, is
caused by random
fluctuations in the signal.
Its modeled by random
values added to an image.
Its
probability
density
function
(pdf) is:
Noise Models:
Gaussian
Noise
Figure: PDF of Gaussian Noise
Example of Gaussian Noise.

13. The Rayleigh distribution
is a continuous probability
distribution for positive
valued random variables.
Rayleigh noise presents in
radar range images.
Its
probability
density
function
(pdf) is:
Noise Models:
Rayleigh
Noise
Figure: Rayleigh Distribution
• mean,  = a+(b/4)1/2
• variance,  = b(4-)/4








azfor
azforeaz
bzp
baz
0
)(
2
)(
/)( 2
Example of Rayleigh Noise.

14. Gamma noise is the
noise which is occurs
in laser imaging and
can be used for
approximating
diagonal histograms. It
obeys the Gamma
distribution.
Its
probability
density
function
(pdf) is:
Noise Models:
Erlang (Gamma)
Noise
Figure: Gamma Distribution









00
0
)!1()(
1
zfor
zfore
b
za
zp
az
bb
• mean, =b/a;
• variance,  =b/a2
Example of Gamma Noise.

15. Its
probability
density
function
(pdf) is:
Noise Models:
Exponential
Noise
Figure: PDF of Exponential NoiseThe exponential
distribution is the
probability distribution
that describes the time
relation between events
in a Poisson process. It
is a particular case of
the gamma distribution







00
0
)(
zfor
zforae
zp
az
In exponential noise model when
b=1 it tends to be Erlang noise
model.
• mean, =1/a;
• variance,  =1/a2
Example of Exponential
Noise.

16. Uniform noise is not often
encountered in real-world
imaging systems, but
provides a useful
comparison with Gaussian
noise. This implies that
nonlinear filters should be
better at removing uniform
noise than Gaussian noise.
Its
probability
density
function
(pdf) is:
Noise Models:
Uniform
Noise
Figure: PDF of Uniform Noise






otherwise
bzafor
abzp
0
1
)(
mean, =(a+b)/2;
variance,  =(b-a)2
/12
Example of Uniform Noise.

17. Its
probability
density
function
(pdf) is:
Noise Models: Impulse
(Salt and Pepper)
Noise
Figure: PDF of Impulse Noise








otherwise
bzfor
azfor
P
P
zp b
a
0
)(
It known as shot noise, impulse
noise or Spike noise .
Its appearance is randomly
scattered white or black or both
pixel over the image .
There are only two possible values
exists that is a and b
and the probability of each is less
than 0.2 .

18. Effects of
Noise on
Images &
Histograms

19. Spatially Dependent Noise Models: Periodic Noise (Example)
Periodic noise
usually arises from
electrical or
electromechanical
interference.
It can be
reduced
significantly
via frequency
domain
filtering.

20. Estimation of Noise Parameters
0
1
P e r i o d i c
N o i s e :The parameters of this
are estimated by Fourier
spectral components.
O n l y A v a i l i t y
o f I m a g e s :
It estimates the noise of
PDF from small patches
of reasonably constant
gray level.
A v a i l i t y o f
I m a g i n g S y s t e m :
It is the simple way to study the
characteristics of system noise
by acquiring a set of images of
flat environment under uniform
illumination (consistent
background).

21. Example
Once the PDF model is
determined, estimate the
model parameters
(mean  , variance 𝜎2).
Estimation of Noise Parameters(Contd.)

22. E x p o n e n t i a l
N o i s e :
Used to model noise in laser
imaging.
A p p l i c a b i l i t y
o f V a r i o u s
N o i s e M o d e l s
U n i f o r m N o i s e :
Used in simulations.
I m p u l s e N o i s e :
Quick transients take place
during imaging.
G a u s s i a n N o i s e :
Electronic circuit noise and sensor
noise due to poor illumination or
high temperature.
R a y l e i g h N o i s e :
Characterize noise in range
imaging.
E r l a n g N o i s e :
Noise in laser imaging.

23. Conclusion
Therefore, noise is added to the image during image
acquisition and to a lesser or greater extent affects the
image. So, the noise models are an important part of
digital image processing. Without having the knowledge
about these models it is nearly impossible to remove the
noise from the image and perform denoising actions.