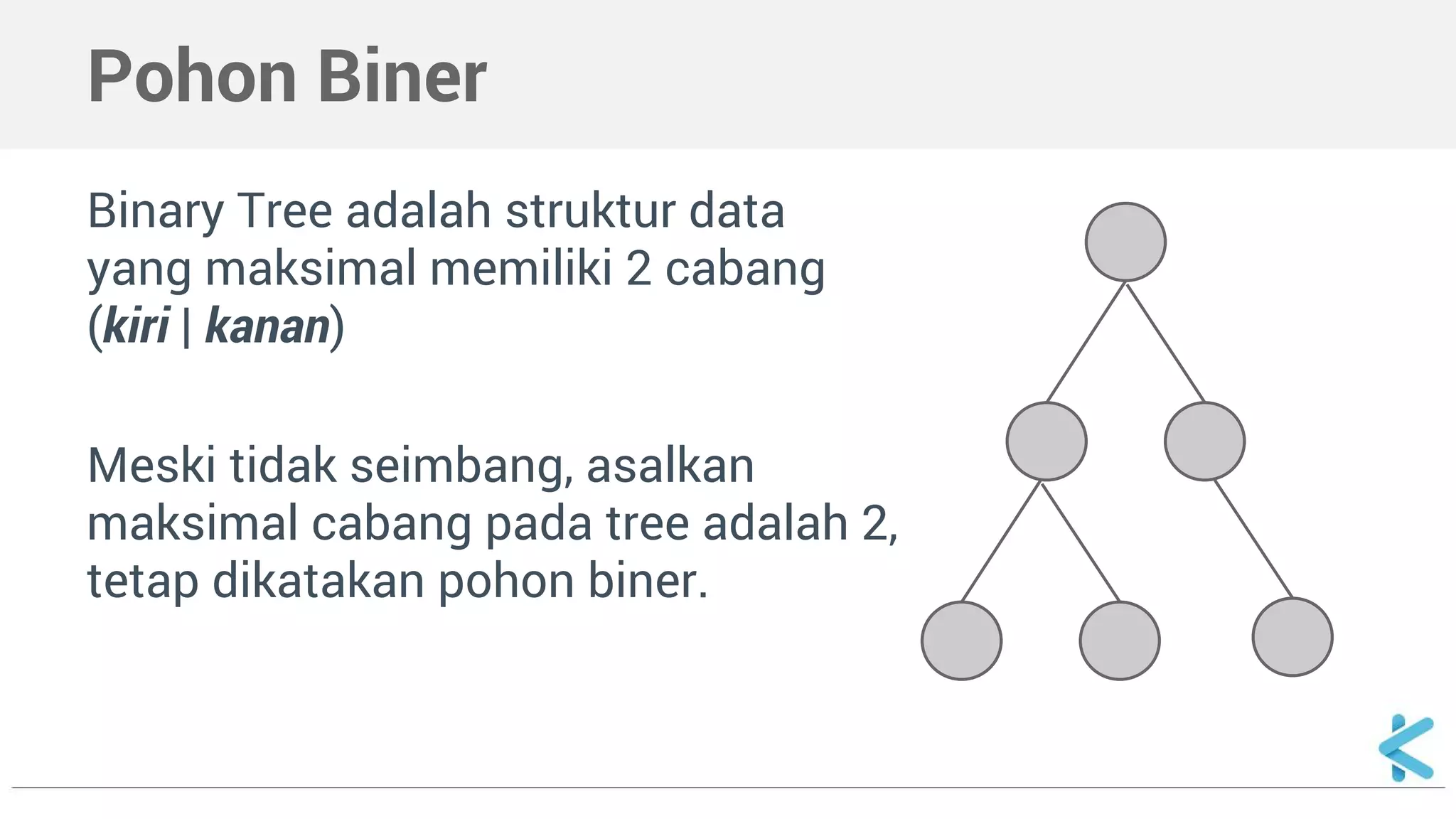
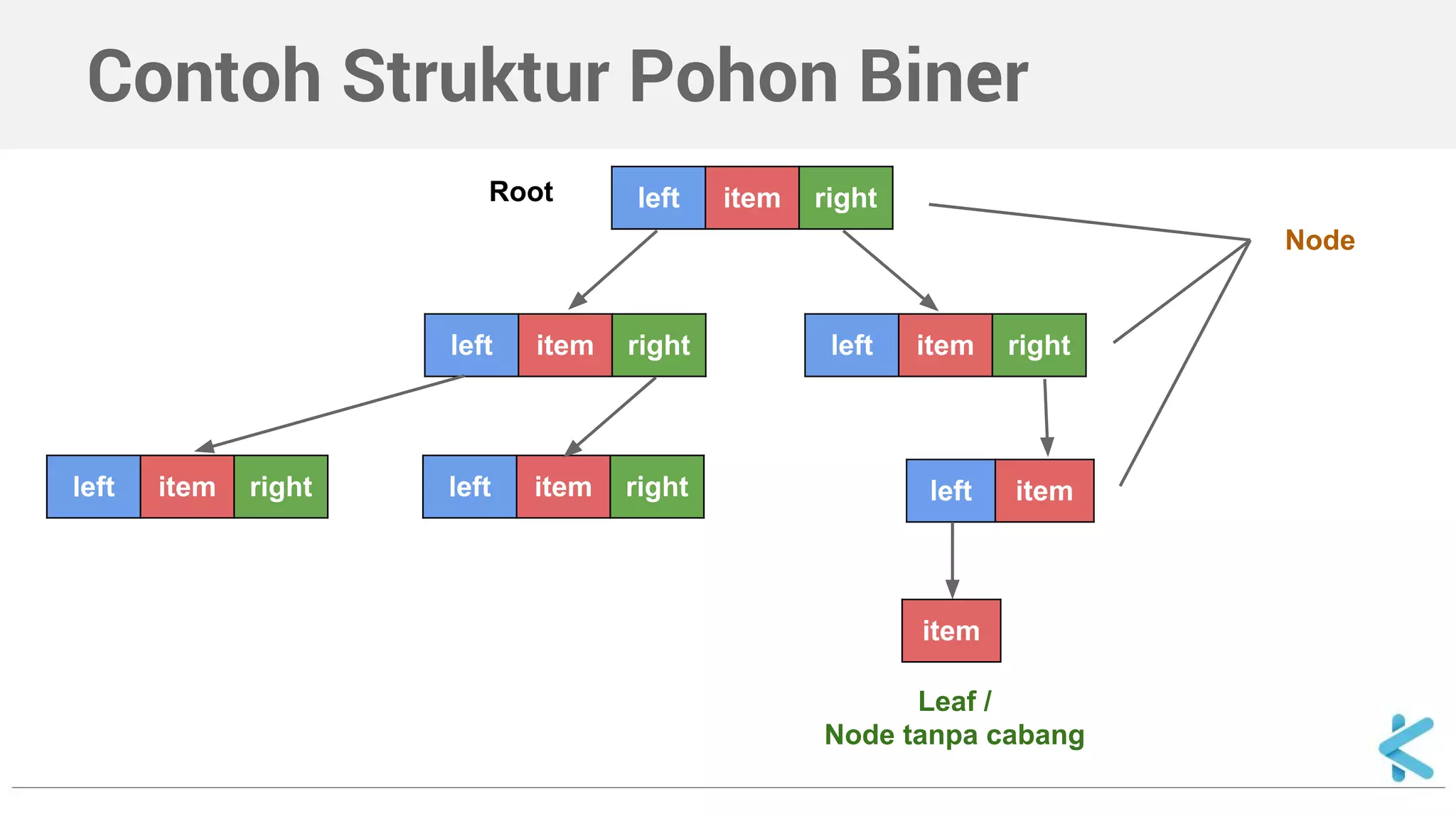
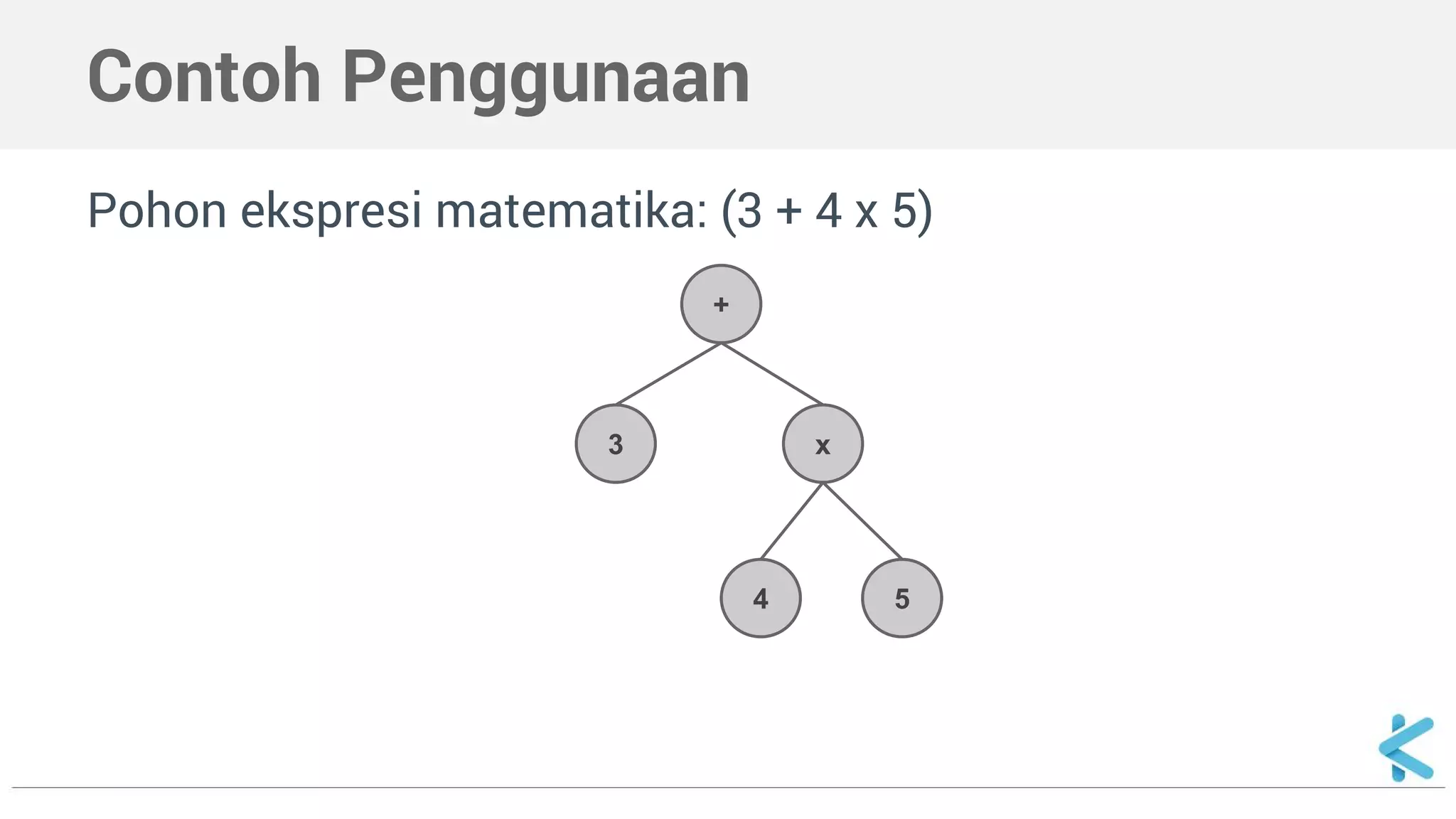
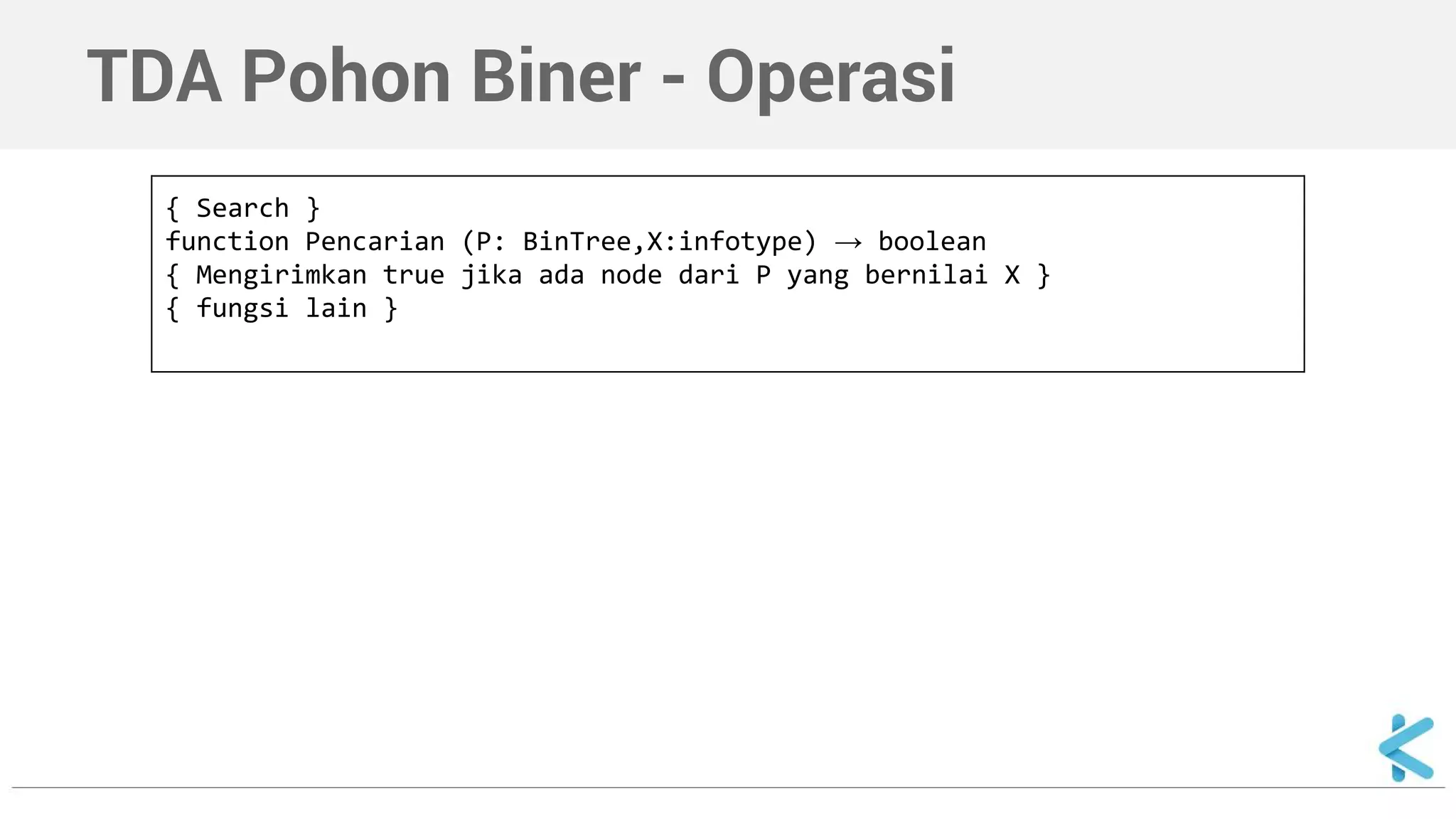
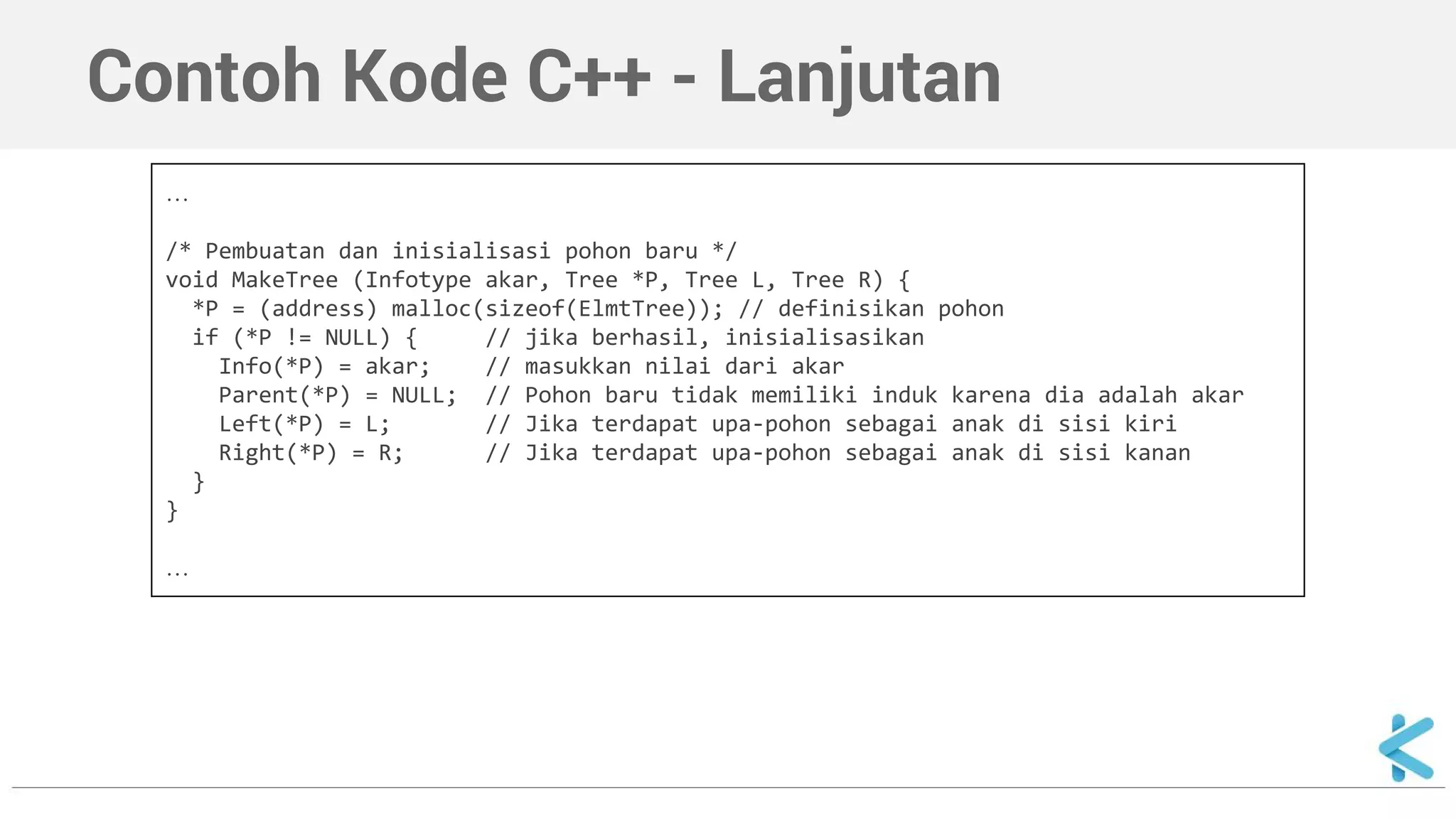
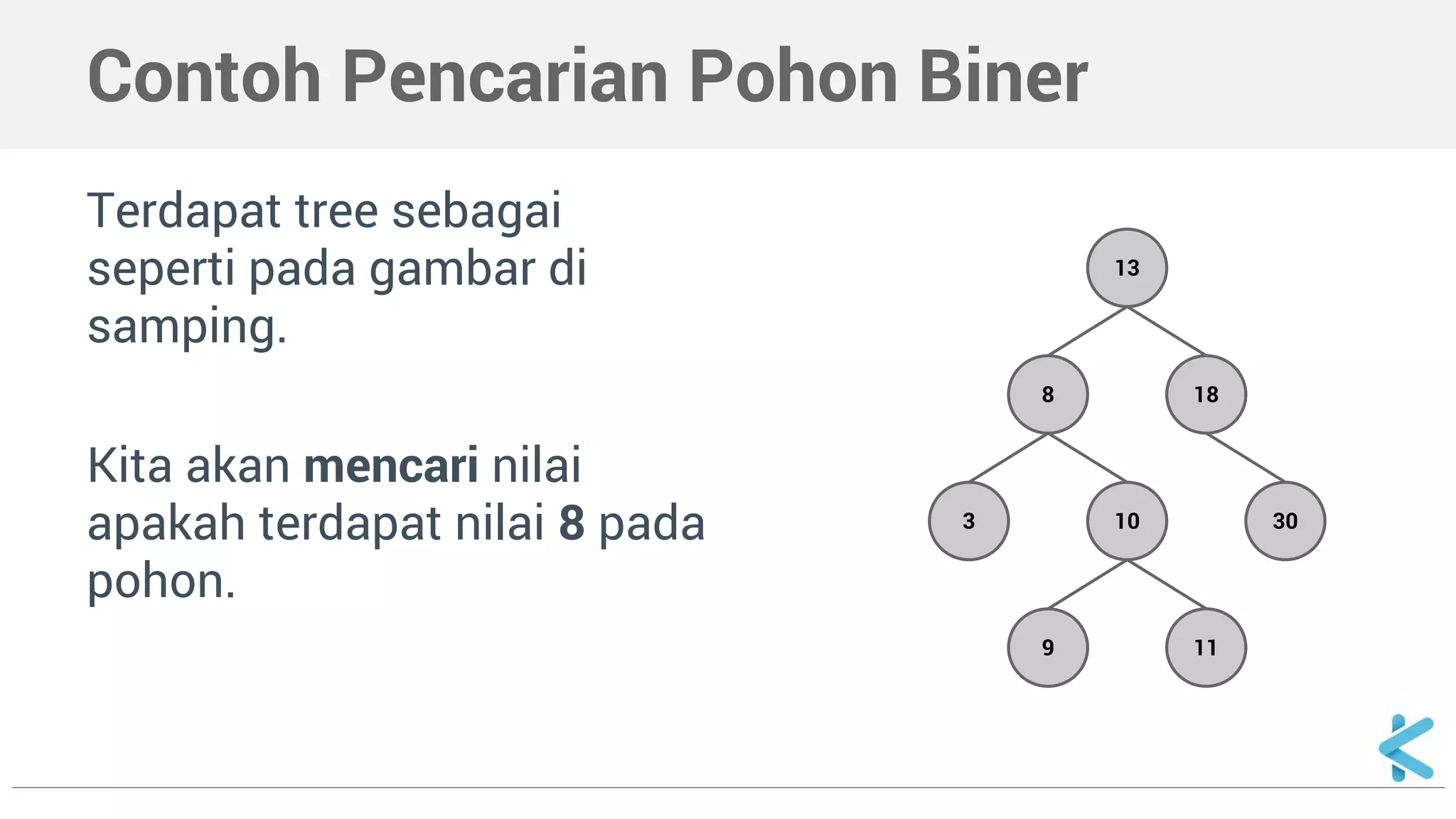
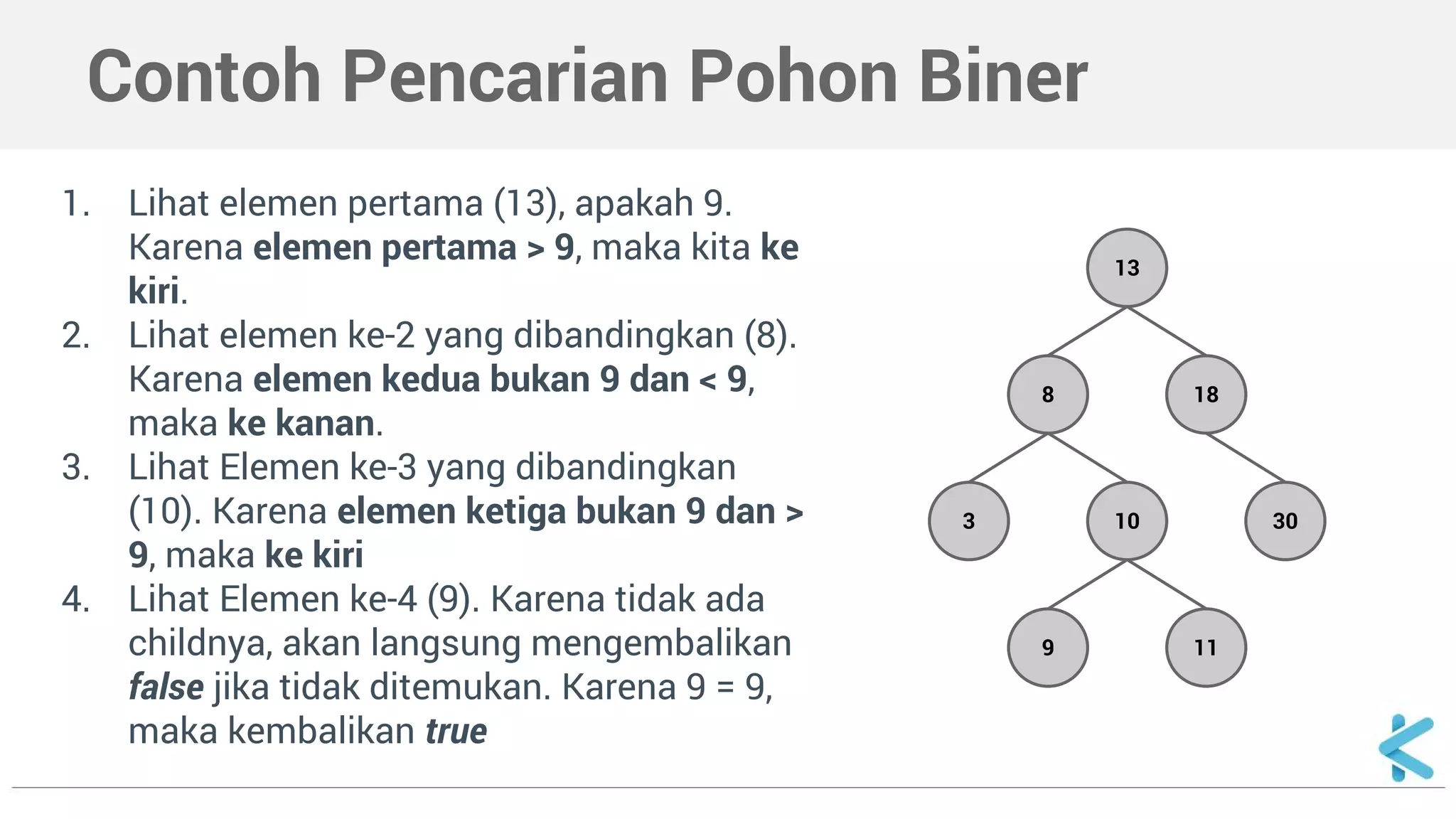
Dokumen ini menjelaskan tentang pohon biner sebagai struktur data dengan dua cabang maksimum (kiri dan kanan) per simpul dan mencakup cara deklarasi serta implementasi dalam C++. Selain itu, dokumen ini juga menyajikan contoh fungsi untuk mencari nilai dalam pohon biner secara rekursif.

1. Pohon Biner
Algoritma dan
Struktur Data
Georgius Rinaldo
dodo@kuliahkita.com

2. Pohon Biner
Binary Tree adalah struktur data
yang maksimal memiliki 2 cabang
(kiri | kanan)
Meski tidak seimbang, asalkan
maksimal cabang pada tree adalah 2,
tetap dikatakan pohon biner.

3. Sifat Pohon Biner
Binary mungkin kosong atau terdiri dari sebuah akar dan
dua anak dengan lebar maksimal 2 pada tiap levelnya,
akan tetapi tidak memiliki batas kedalaman.
Apabila sebuah pohon memiliki sub-tree pada salah satu
sisi yang lebih banyak maka pohon tersebut disebut pohon
condong - kiri atau kanan (skewed tree)

4. Contoh Struktur Pohon Biner
left item right
left item right left item right
left item right left item right left item
item
Root
Node
Leaf /
Node tanpa cabang

5. Contoh Penggunaan
Pohon ekspresi matematika: (3 + 4 x 5)
+
3 x
4 5

6. TDA Pohon Biner
{ Deklarasi Type }
type node < info : infotype,
left : address,
right : address >
type BinTree : address
type Elmtnode < info : infotype,
Next : address>
type ListofNode : address { list linier yang elemennya Elmtnode }

7. Penjelasan TDA Pohon Biner
Pohon biner memiliki konsep yang mirip dengan senarai
atau list.
Perbedaannya, pada list hanya dihubungkan tepat satu
buah simpul sedangkan pohon biner menghubungkan dua
buah simpul yaitu left dan right.
Jika pohon biasa, maka simpul yang dihubungkan dapat
berjumlah lebih dari dua.

8. Penjelasan TDA Pohon Biner - 2
Simpul pada pohon biner terdapat info yang menyimpan
informasi dengan tipe tertentu seperti list.
Selain itu juga terdapat right dan left, yang menyimpan
alamat dari simpul berikutnya. Dengan begitu sebuah
simpul dapat terhubung dengan simpul.
Terdapat juga sebuah parent yang menunjuk alamat dari
induk simpulnya. Dengan parent, simpul dapat menelusuri
ke dua arah yaitu ke anaknya dan induknya.

9. TDA Pohon Biner - Primitif
{ Inisialisasi }
procedure MakeTree (input Akar:infotype, input/output P: BinTree, L:
BinTree, R:BinTree)
{ I.S. sembarang }
{ F.S. Menghasilkan sebuah pohon P }
{Menghasilkan sebuah pohon biner P dari A, L dan R , jika alokasi
berhasil}
{Menghasilkan pohon P yang kosong (Nil) jika alokasi gagal }
{ PRIMITIF }
{ Selektor }
function GetAkar (P: BinTree) → infotype
{ Mengirimkan nilai Akar pohon biner P }
function GetLeft (P: BinTree) → BinTree
{ Mengirimkan Anak Kiri pohon biner P }
function GetRight (P: BinTree) → BinTree
{ Mengirimkan Anak Kanan pohon biner P }

10. TDA Pohon Biner - Operasi
{ Search }
function Pencarian (P: BinTree,X:infotype) → boolean
{ Mengirimkan true jika ada node dari P yang bernilai X }
{ fungsi lain }

11. Contoh Kode C++
#include <iostream>
using namespace std;
typedef char Infotype; // Infotype didefinisikan sebagai alias dari tipe karakter
typedef struct tElmtTree *address;
typedef struct tElmtTree {
Infotype Info; // Info adalah informasi dari sebuah simpul pohon bertipe Infotype yang
terdefinisi
address Left; // Cabang kiri dari sebuah pohon bertipe alamat menuju ke sebuah simpul kiri
address Right; // Cabang kanan juga memilikit tipe alamat menuju sebuah simpul
address Parent; // Parent adalah alamat dari sebuah simpul yang posisinya di atas dirinya
} ElmtTree; // Semua ini dibungkus dalam sebuah tipe dan merupakan definisi dari simpul
#define Info(P) (P)->Info
#define Left(P) (P)->Left
#define Right(P) (P)->Right
#define Parent(P) (P)->Parent

12. Contoh Kode C++ - Lanjutan
...
/* Pembuatan simpul baru */
ElmtTree buatSimpul(Infotype x) {
ElmtTree elem; // definisikan ElmtList sebagai simpul
elem.Info = x; // isi informasi pada simpul
elem.Left = NULL; // alamat left dan right baru adalah kosong atau NULL
elem.Right = NULL; // alamat next dari simpul yang baru adalah kosong atau NULL
elem.Parent = NULL; // alamat next dari simpul yang baru adalah kosong atau NULL
return elem;
}
...

13. Contoh Kode C++ - Lanjutan
…
/* Pembuatan dan inisialisasi pohon baru */
void MakeTree (Infotype akar, Tree *P, Tree L, Tree R) {
*P = (address) malloc(sizeof(ElmtTree)); // definisikan pohon
if (*P != NULL) { // jika berhasil, inisialisasikan
Info(*P) = akar; // masukkan nilai dari akar
Parent(*P) = NULL; // Pohon baru tidak memiliki induk karena dia adalah akar
Left(*P) = L; // Jika terdapat upa-pohon sebagai anak di sisi kiri
Right(*P) = R; // Jika terdapat upa-pohon sebagai anak di sisi kanan
}
}
…

14. Contoh Kode C++ - Lanjutan
…
int main(){
ElmtTree akar = buatSimpul('X');
ElmtTree node1 = buatSimpul('A');
ElmtTree node2 = buatSimpul('B');
Tree T1,T2,T3;
// Inisialisasi instan
T2 = &node2; // menghasilkan null pada anak kiri dan kanan
T3 = &node3;
// Inisialisasi Lengkapnya dengan
MakeTree('A', &T2, NULL, NULL);
MakeTree('B', &T2, NULL, NULL);
MakeTree('Z', &T1, T2, T3);
cout << T1->Left->Info;
return 0;
}

15. Contoh Pencarian Pohon Biner
Terdapat tree sebagai
seperti pada gambar di
samping.
Kita akan mencari nilai
apakah terdapat nilai 8 pada
pohon.
13
8 18
3 10
9 11
30

16. Contoh Pencarian Pohon Biner
1. Lihat elemen pertama (13), apakah 9.
Karena elemen pertama > 9, maka kita ke
kiri.
2. Lihat elemen ke-2 yang dibandingkan (8).
Karena elemen kedua bukan 9 dan < 9,
maka ke kanan.
3. Lihat Elemen ke-3 yang dibandingkan
(10). Karena elemen ketiga bukan 9 dan >
9, maka ke kiri
4. Lihat Elemen ke-4 (9). Karena tidak ada
childnya, akan langsung mengembalikan
false jika tidak ditemukan. Karena 9 = 9,
maka kembalikan true
13
8 18
3 10
9 11
30

17. Pencarian Pohon Biner
Pencarian terhadap binary tree dilakukan secara rekursif.
Berikut adalah pseudocodenya.
function pencarianBinaryTree(key, node)
/* Jika elemen pada node atau key = nilai yang dicari -> sebagai basis */
if node = Null or node.key = key then
return node
else if key < node.key then
return pencarianBinaryTree(key, node.left)
else
return pencarianBinaryTree(key, node.right)
end if

18. Pencarian Pohon Biner
Berikut contoh implementasi sederhana dalam fungsi C++
node search(int key, node *leaf) {
if(leaf != NULL) {
if(key == leaf->Info)
return leaf;
if(key < leaf->Info)
return search(key, leaf->Left);
else
return search(key, leaf->Right);
}
else return NULL;
}