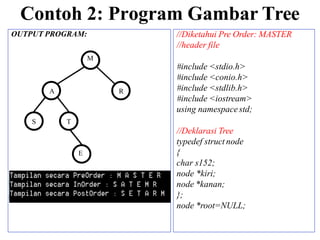
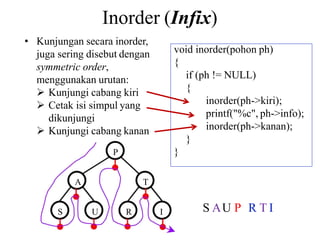
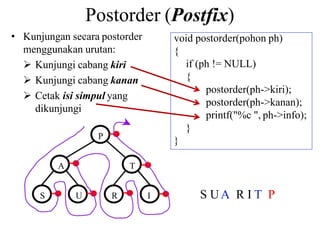
Dokumen ini menjelaskan tentang struktur data pohon, termasuk definisi, jenis, dan cara traversal pada pohon biner. Pohon digunakan untuk mengorganisir informasi secara hierarkis dan pohon biner adalah yang paling umum digunakan, dengan setiap simpul memiliki maksimal dua anak. Berbagai metode traversal seperti preorder, inorder, dan postorder juga diuraikan beserta contoh implementasinya dalam kode.










![Contoh traversal
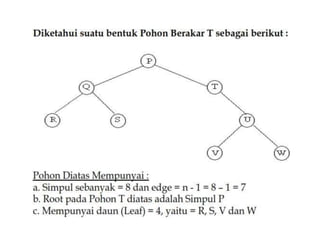
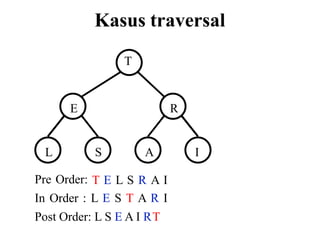
Tentukan traversal tree dari tree: [ A ^ (B - C) / (E * F) +G]
Maka:
Pre Order = /^-BCA+*EFG
In Order = B-C^A/E*F+G
Post Order = BC-A^EF*G+/
Perhatikan operator dengan
operasi terbanyak/terberat
akan sebagai ROOT.
Persamaan In Order adalah
mirip dengan traversal.](https://image.slidesharecdn.com/13-240612052531-52d7ee1c/85/power-point-struktur-data-tree-atau-pohon-19-320.jpg)



![Sambungan …#2
if(root!=NULL)
{
inOrder(root->kiri);
if(root->data!=NULL)
{
printf("%d ",root->data);
}
inOrder(root->kanan);
}
}
//fungsi yang digunakan untuk mencetak tree
secara postOrder
void postOrder(Node *root)
{
if(root!=NULL) {
postOrder(root->kiri);
postOrder(root->kanan);
if(root->data!=NULL)
{
printf("%d ",root->data); }
}
}
//fungsi utama
int main()
{
//deklarasikan variabel
char pil;
while (true)
{
system("cls"); //bersihkan layar
char data;
printf("t#PROGRAM TREE Dev C++#");
printf("nt=================");
printf("nMENU");
printf("n----n");
printf("[1] Tambah Datan");
printf("[2] Lihat Pre-Ordern");
printf("[3] Lihat In-Ordern");
printf("[4] Lihat Post-Ordern");
printf("[X] Keluarn");
printf("Pilihan Anda : ");
scanf("%c",&pil);
fflush(stdin); //mengosongkan buffering](https://image.slidesharecdn.com/13-240612052531-52d7ee1c/85/power-point-struktur-data-tree-atau-pohon-23-320.jpg)