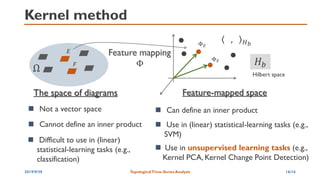
The document discusses topological time-series data analysis using delay-variant embedding, emphasizing the importance of understanding complex data structures through topological features. It introduces concepts such as persistent homology and the significance of holes in high-dimensional spaces, illustrating methods for analyzing time-series data dynamics. The proposed delay-variant embedding method aims to enhance the representation of time-series characteristics in a robust way against noise perturbations.

1. Topological Time-Series Data Analysis with
Delay-Variant Embedding
The University ofTokyo
CCS2019@NTU
zoro@biom.t.u-tokyo.ac.jp
Graduate School of Information Science andTechnology
Tran Quoc Hoan (Ph.D. Candidate)

2. Motivation
Diagram of the hierarchical organization of biology at different scales and examples of data that can be collected at these different levels.
(Image source https://researcher.watson.ibm.com/researcher/view_group.php?id=5372)
E.g.,Variant scales of biology
◼ Reveal the black box (vs.
Deep Learning machines) to
understand the nature of
complex data
◼ Reveal the variant scales in
complex data
2019/9/30 TopologicalTime-SeriesAnalysis 2/16

3. VariantTopological Features
◼ Our research focuses on the shape of data to provide
insights into dynamics, variant scales via new and
general features which are robust under the perturbation
applied to the data.
◼ The “shape” of data
→ Appearance of holes in the high-dimensional space
◼ Dynamics &Variant scales
→ Oscillations, variant timescales.
◼ Perturbation
→ Noise added to data
2019/9/30
We focus on time-
series data in this talk
TopologicalTime-SeriesAnalysis 3/16

4. Persistent Homology
◼ An algebraic method to encode the topological structures
of data into quantitative features
Finite set of points, networks, etc.
We need
i.e., holes
➢ Mathematically define the “hole”
➢ Quantitatively calculate the “hole”
2019/9/30 TopologicalTime-SeriesAnalysis 4/16

5. 2019/9/30 Topological Time-Series Analysis 5/24

6. What is hole?
◼ 0-dimensional holes: connected components
◼ 1-dimensional holes: rings, loops, tunnels
1-dimensional graph (in 𝐾) without
boundary, they are not boundary of
any 2-dimensional graph in 𝐾
Not a hole
𝐾
A hole
◼ 2-dimensional holes: cavities, voids
2-dimensional graph (in 𝐾) without
boundary, they are not boundary of
any 3-dimensional graph in 𝐾 Not a hole
solid
empty
A hole
2019/9/30 TopologicalTime-SeriesAnalysis 6/16

7. Represent the “hole”
◼ Idea: connect nearby points, fill in complete geometrical
shapes
𝜀
1. Choose
a distance
𝜀.
2. Connect
pairs of
points that
are no further
apart than 𝜀.
3. Fill in complete
geometrical shapes
(triangle, tetrahedron, etc.).
4. Homology detects the hole
Problem:
How do we choose
the distance 𝜀
2019/9/30 This figure is designed similarly with the slide “Introduction to Persistent Homology” of Dr. Matthew L.Wright 7/16

8. 𝜀
How to choose distance 𝜀?
This 𝜀
looks
good.
Innovation Idea
Consider all
distances 𝜀.
How to
distinguish
this hole with
other ?
2019/9/30 8/16
This figure is designed similarly with the slide “Introduction to Persistent Homology” of Dr. Matthew L.Wright

9. 𝜀: 0 1 2 3
Barcodes: Monitor the change of topological structures
2019/9/30 9/16
This figure is designed similarly with the slide “Introduction to Persistent Homology” of Dr. Matthew L.Wright

10. Topological features = Persistence Diagram
A persistence diagram is a two-
dimensional representation of a
barcode
◼ Multi-set points with coordinates (b,
d) which represent birth-scale (b) and
death-scale (d) of the hole.
Birth-scale
Death-scale
2019/9/30 TopologicalTime-SeriesAnalysis 10/16

11. Time-series reconstruction
◼ Situation: Dynamics and variant
scales of time-series data
◼ Oscillations,chaotic
◼ Variant time scales
𝑋(𝑚)
𝜏
𝑡 = 𝑥 𝑡 , 𝑥 𝑡 − 𝜏 , … , 𝑥 𝑡 − 𝑚 − 1 𝜏
𝑋(𝑚)
𝜏
1
𝑥 𝑡
𝑥 𝑡 − 2𝜏 𝑥 𝑡 − 𝜏
𝑋(𝑚)
𝜏
2
𝑋(𝑚)
𝜏
3
𝜏
𝜏
𝜏 𝜏
𝜏
𝜏
𝑥 𝑡
𝑋(𝑚)
𝜏
1
𝑋(𝑚)
𝜏
2
𝑋 𝑚
𝜏
(3)
Delay embedding
(Taken’s theorem)
Transform timeseries to finite set
of points in high-dimensional space
2019/9/30 TopologicalTime-SeriesAnalysis 11/16

12. Patterns from delay-embedding
Limit cycle
Limit torus Strange attractor
(Topological) Patterns
from delay-embedding
represent the behavior
of attractors which
provide insights into
dynamical system
Attractors of Dynamical System
Fixed point
2019/9/30 TopologicalTime-SeriesAnalysis 12/16

13. Problem in delay-embedding
Determining time delay is sensitive and problem-dependent
◼ Well-known methods: mutual information, auto correlation, etc
◼ A real timeseries is noisy and has a finite length
It is not well-defined to
evaluate the shape of
embedded points from
embedding space
2019/9/30 TopologicalTime-SeriesAnalysis 13/16

14. (Proposed) Delay-variant embedding
◼ Considering time delay 𝜏
as the variable parameter
◼ Monitor the variation of
topological structures in
the embedded space
◼ Construct the
topological features for
each 𝜏, then integrate
these features with
𝜏 serving as an additional
dimension
𝑥(𝑡)
𝑥(𝑡)
𝑥(𝑡 − 𝜏)
𝑥(𝑡 − 2𝜏)
2019/9/30 TopologicalTime-SeriesAnalysis
Three-dimensional persistence diagram (3PD)
14/16

15. Stability theorem
𝑑𝐵,𝜉
(3)
𝐷(𝑙,𝑚)
(3)
𝑥 , 𝐷(𝑙,𝑚)
(3)
𝑦 ≤ 2 𝑚 max
𝑡∈𝕋
𝑥 𝑡 − 𝑦(𝑡)
Theorem: Stability theorem
◼ If 𝑥 𝑡 is perturbed by noise to 𝑦 𝑡 = 𝑥 𝑡 + 𝜖(𝑡) then the upper limit
of the distance between diagrams is governed by magnitude of 𝜖(𝑡)
◼ The 3PDs are robust w.r.t time-series data being perturbed by noise
◼ The 3PDs can be used as discriminating features for characterizing the
time series
2019/9/30 TopologicalTime-SeriesAnalysis 15/24

16. Kernel method
◼ Can define an inner product
◼ Use in (linear) statistical-learning tasks (e.g.,
SVM)
𝐸
𝐹
The space of diagrams
◼ Not a vector space
◼ Difficult to use in (linear)
statistical-learning tasks (e.g.,
classification)
◼ Cannot define an inner product
Ω
Φ𝐸
Φ𝐹
, 𝐻𝑏
Feature mapping
Φ
Feature-mapped space
𝐻𝑏
Hilbert space
◼ Use in unsupervised learning tasks (e.g.,
Kernel PCA, Kernel Change Point Detection)
2019/9/30 TopologicalTime-SeriesAnalysis 16/16

17. Scenarios for Applications
◼ Identify the dynamics of
biological model via observed
noisy biological timeseries
➢ E.g., stochastic oscillations in
single-cell live imaging time
series
◼ Classify real time-series data
➢ E.g., ECG data, sensor data
(Image source https://slideplayer.com/slide/7612898/ )
Stochastic model of the Hes1
genetic oscillator (N.A. Monk,
Curr. Biol. 13, 2003)
2019/9/30 17/16
Topological time-series analysis with delay-variant embedding, Physical Review E 100, 032308, 2019

18. 2019/9/30 Topological Time-Series Analysis 18/16

19. Thanks for
listening!