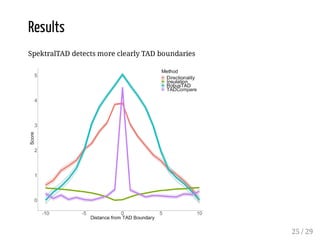
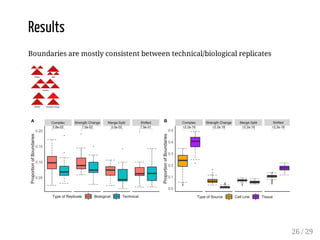
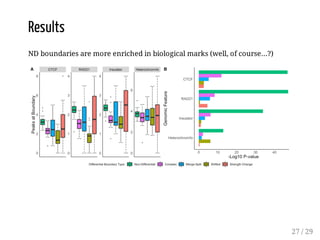
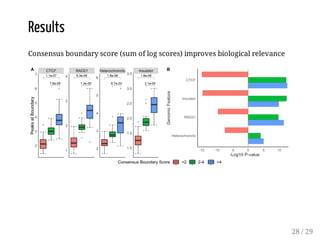
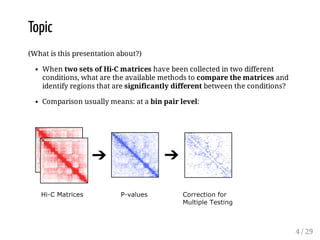
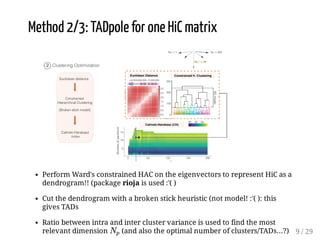
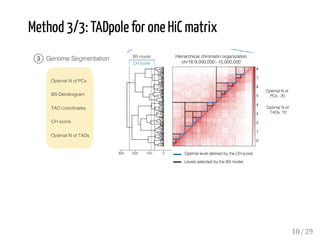
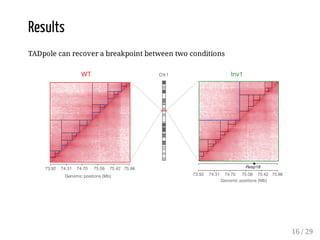
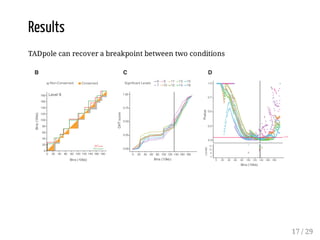
When Hi-C matrices are collected from two different conditions, methods can compare the matrices to identify regions with significant structural differences between conditions. TADpole and TADcompare are two available methods. TADpole represents hierarchical TAD structures and detects differences by computing a difference index between normalized binarized matrices. TADcompare represents Hi-C matrices as networks and uses the eigenvectors of the graph Laplacian and gap scores to define boundaries and detect differential boundaries between conditions. Both methods were shown to recover known breakpoints and have boundaries enriched for biological marks.

1. Di erential analyses of structures in HiCDi erential analyses of structures in HiC
datadata
Nathalie Vialaneix, INRAE/MIATNathalie Vialaneix, INRAE/MIAT
Chrocogen, November 13th, 2020Chrocogen, November 13th, 2020
1 / 291 / 29

2.
2 / 292 / 29

3. Description ofthe scope ofthe articlesDescription ofthe scope ofthe articles
3 / 293 / 29

4. Topic
(What is this presentation about?)
When two sets of Hi-C matrices have been collected in two different
conditions, what are the available methods to compare the matrices and
identify regions that are significantly different between the conditions?
Comparison usually means: at a bin pair level:
4 / 29

5. Topic
(What is this presentation about?)
When two sets of Hi-C matrices have been collected in two different
conditions, what are the available methods to compare the matrices and
identify regions that are significantly different between the conditions?
Comparison usually means: at a bin pair level but here: structure level
(differences between TADs or TAD boundaries)
5 / 29

6. TADpoleTADpole
6 / 296 / 29

7. Main features
R package available on github (only?)
Main purpose of TADpole: represent the hierarchical structure of TAD,
sub-TADs and meta-TADs. Can secondarily be used to detect differences
between TADs
7 / 29

8. Method 1/3: TADpole for one HiCmatrix
remove "bad columns"
compute correlation matrix
perform PCA using the rows of as a representation of the bins extract
eigenvectors ( representation of bins as elements of )
Warning: Since 1/ is not sparse and 2/ PCA is expensive, the approach is
performed on half chromosomes (centromere is estimated using the
correlation)
Σ
Σ ⇒
Np ∼ R
Np
Σ
8 / 29

9. Method 2/3: TADpole for one HiCmatrix
Perform Ward's constrained HAC on the eigenvectors to represent HiC as a
dendrogram!! (package rioja is used :'( )
Cut the dendrogram with a broken stick heuristic (not model! :'( ): this
gives TADs
Ratio between intra and inter cluster variance is used to find the most
relevant dimension (and also the optimal number of clusters/TADs...?)Np 9 / 29

10. Method 3/3: TADpole for one HiCmatrix
10 / 29

11. Howto use TADpole for comparing matrices?
Framework: 2 matrices, one in each condition. TADpole has been used on
each of them
Computing a difference index between matrix and matrix for a given
bin : where:
: entry of binarized HiC matrix ($i$ and are in the same cluster)
this quantity is normalized to stay between 0 and 1
Personal note: I don't get why the quantity is summed over the beginning of
the matrix... ( )
H
1
H
2
b D(H
1
, H
2
)(b) = ∑
i≤b
∑
p
j=1
|
~
h
1
ij
−
~
h
2
ij
|
~
h
k
ij
(i, j) j
∑
i<b
11 / 29

12. p-value derivation
Random test:
generate random partitions (clusters)
compute the Diff statistics between and the random partitions -
value for bin (in practice used only on a 2Gb portion of the genome)
Note: this is not symmetric between and !
10
4
H
1
⇒ p
b
H
1
H
2
12 / 29

13. Evaluation
1. One HiC dataset transformed into 24 HiC matrices (four resolutions 2
normalization + raw data and 12 down-sampling of one of the matrix)
used for: comparing several TAD callers (as in [Zufferey et al, 2018])
by comparing domains accross different resolutions
by measuring the concordance between two partitions (MI measure)
by assessing the computational performances of the tools
by using biological evidences (histone mark or structural protein profiles,
FC at TAD boundaries, ratio of TAD boundaries hosting a SP, ratio of ChIP-
seq signals in TAD bodies)
1. Two cHiC experiments (one chromosome, one genomic interval), based
on the two homozygous strains (mouse, embryonic), one WT and one
mutant
×
13 / 29

14. Results
TADpole gives replicable results
14 / 29

15. Results
TADpole is in accordance with biological evidence
15 / 29

16. Results
TADpole can recover a breakpoint between two conditions
16 / 29

17. Results
TADpole can recover a breakpoint between two conditions
17 / 29

18. TADcompareTADcompare
18 / 2918 / 29

19. Main features
R package available on github (and submitted to Bioconductor)
by the same authors than HicCompare and multiHicCompare (based on
MD corrections)
Main purpose of TADcompare: represent the HiC matrices as networks
and derive a bin gap score to detect boundaries (same exact idea than in
[Cresswell et al., 2020] on SpectralTAD). Use that score to derive
differential boundaries
19 / 29

20. Method: connexion to spectral clustering
Main idea: HiC matrix is a graph so use tools dedicated to graphs.
Laplacian of a graph: (where is the HiC matrix without
its diagonal and )
Laplacian, graph structure and spectral clustering (see [von Luxburg, 2007]):
eigenvectors associated to eigenvalue 0 gives the connected components
of the graph
L = D
−1/2
HD
1−2
H
D = Diag(1
⊤
p
H)
20 / 29

21. Method: connexion to spectral clustering
Main idea: HiC matrix is a graph so use tools dedicated to graphs.
Laplacian of a graph: (where is the HiC matrix
without its diagonal and )
Laplacian, graph structure and spectral clustering (see [von Luxburg, 2007]):
eigenvectors associated to eigenvalue 0 gives the connected components
of the graph
other eigenvalues are and corresponding
eigenvectors provide increasingly noisy information about the main
structures (clusters) in the graph
spectral clustering: take the first eigenvectors (smallest eigenvalues) and
use them as representations of graph nodes (here, bins) in for -means
L = D
−1/2
(D − H)D
1−2
H
D = Diag(1
⊤
p
H)
0 < λ1 < λ2 <. . . < λp−k
d
R
d
k
21 / 29

22. TADcompare method
compute eigen-decomposition of and extract the first 2 eigenvectors
(length: )
replace the HiC matrix by a representation of the bins with (so bin
is in , )
cuisine: normalization: (I guess but very unclear in both
articles)
distance between bins and (called gap score of ):
(again, very unclearly written)
magic trick: this is distributed as a log-normal...
boundary scores: (said to follow which is not
true... because would be the proper score)
more cuisine: spectral decomposition is performed with sliding windows
of 15 bins to avoid having to handle a large spectral decomposition
L
(v1 , v2 ) p
[v1 , v2 ]
i R
2
v
i
z
i
=
v
i
∥v
i
∥
i i − 1 i
Di = ∥v
i
− v
i−1
∥
log Di ∼ N (μ, σ) ⇒
Bi =
log Di−μ
σ
2
N (0, 1)
log Di−μ
σ
22 / 29

23. Using the approach to detect di erential TADs
two matrices: are gap scores of bin for matrix
pseudo-maths: (note: this is
not true in general...)
new differential boundary scores: (also said to follow
) -values
Time course version: monitor medians of differential scores with
accross multiple replicates and identify breaks in this values
D
k
i
i k ∈ {1, 2}
log(D
1
i
) − log(D
2
i
) ∼ N (μ1 − μ2 , σ
2
1
+ σ
2
2
)
DBi =
σ
2
1
B
1
i
−σ
2
2
B
2
i
σ
2
1
+σ
2
2
N (0, 1) ⇒ p
t = 0
23 / 29

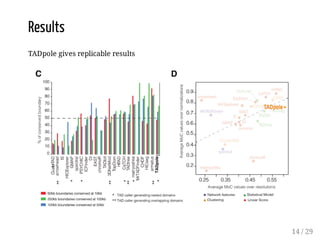
24. Evaluation
The method is evaluated for:
boundary discovery (enrichment in proteins with permutation tests)
boundary difference discovery (also colocalized boundaries enrichment
with permutation tests)
Data: from [Forcato et al, 2017] (repository), time course data from human
colon cancer cell line at four time points after auxin treatment
Scripts: R package on Bioconductor + scripts in a repository
24 / 29

25. Results
SpektralTAD detects more clearly TAD boundaries
25 / 29

26. Results
Boundaries are mostly consistent between technical/biological replicates
26 / 29

27. Results
ND boundaries are more enriched in biological marks (well, of course...?)
27 / 29

28. Results
Consensus boundary score (sum of log scores) improves biological relevance
28 / 29

29. References
Cresswell KG, Dozmorov MG (2020) TADCompare: an R package for differential and temporal
analysis of topologically associated domains. Frontiers in Genetics 11: 158
Cresswell KG, Stansfield JC and Dozmorov MG (2020) SpectralTAD: an R package for defining
a hierarchy of topologically associated domains using spectral clustering. BMC
Bioinformatics 21: 319
Forcato M, Nicoletti C, Pal K, Livi CM, Ferrari F, Bicciato S (2017) Comparison of
computational methods for Hi-C data analysis. Nature Methods 14: 679-685
von Luxburg U (2007) A Tutorial on Spectral Clustering. Statistics and Computing 17(4): 395-
416
Soler-Vila P, Cuscó P, Farabella I, Di Stefano M, Marti-Renom M.A. (2020) Hierarchical
chromatin organization detected by TADpole. Nucleic Acid Research 48(7): e39
Zufferey M, Tavernari D, Oricchio E, Ciriello G (2018) Comparison of computational methods
for the identification of topologically associated domains. Genome Biology 19: 217-234
29 / 29